에너지시스템 최적화/게임이론 강의: 2) Market clearing as an equilibrium problem
이 포스팅은, Technical University of Denmark의 박사과정 과목 “Advanced Optimization and Game Theory for Energy Systems” (Prof. Jalal Kazempour) 의 2강을 필자가 요약한 내용이다.
최적화 기반 market clearing 결과는 game의 ‘Nash 균형’인가?
지난 강의에서 최적화 문제를 풀어서 각 발전기의 발전량, 각 수요처의 전기부하, 그리고 가격을 결정했다.

그런데, 과연 각 발전사업자와 각 수요처 각자의 입장에서, 해당 최적화 문제의 결과가 ‘받아들일 만한’ 것일까? 받아들이지 못할 결과라면 참가자들이 시장에서 떠나는 (deviate) 문제가 발생할 것이다.
각 발전기는 발전량에 market price를 곱한 revenue에서 발전 비용을 뺀 profit을 최대화하려 할 것이고, 각 수요처는 부하량에 bid price와 market price 간 차이를 곱한 utility를 최대화하려 할 것이다.
위 최적화 결과로 얻은 각 발전기 별 발전량, 각 수요처 별 부하량, 그리고 시장가격이 주어질 경우, 어떤 참가자에 대해서도 (다른 참가자가 현재 상태를 유지한다는 전제 하에) 현재 상태가 profit 또는 utility를 최대화하는 상태여야 한다.
즉 각 발전기와 수요처를 ‘game의 참가자’ 로 볼 때, 위 최적화 문제를 풀어 얻은 결과가 해당 game의 (유일한) Nash 균형이어야 한다.
(‘유일한’ Nash 균형이 아닐 경우 갈등이 생길 수 있다. 어떤 참가자가 “나한테는 균형 1이 더 좋은데 왜 market operator 당신은 균형 2로 결정했냐” 등…)
각 참가자 ‘개별’의 최적화 문제들 모은 Nash 균형 문제를 보면 아래 슬라이드와 같다.

발전기와 수요처 뿐 아니라 price-setter가 있는데, 이는 수요-공급 균형 제약을 고려하면서 동시에 가격을 결정하기 위한 가상의 참가자이다.
전력시장의 Nash 균형 문제는 최적화 문제와 동치이다
최적화 문제를 풀어 얻은 결과가 Nash 균형인지 여부를 판단하려면, 최적화 문제와 Nash 균형 문제가 수학적으로 동치 (equivalent problem) 인지 여부를 판단할 수 있는 비교가 필요하다.
이를 위해서는, 최적화 문제의 KKT (Karush-Kuhn-Tucker) condition과 Nash 균형 문제의 각 참가자 별 KKT condition들의 모음을 서로 비교한다.
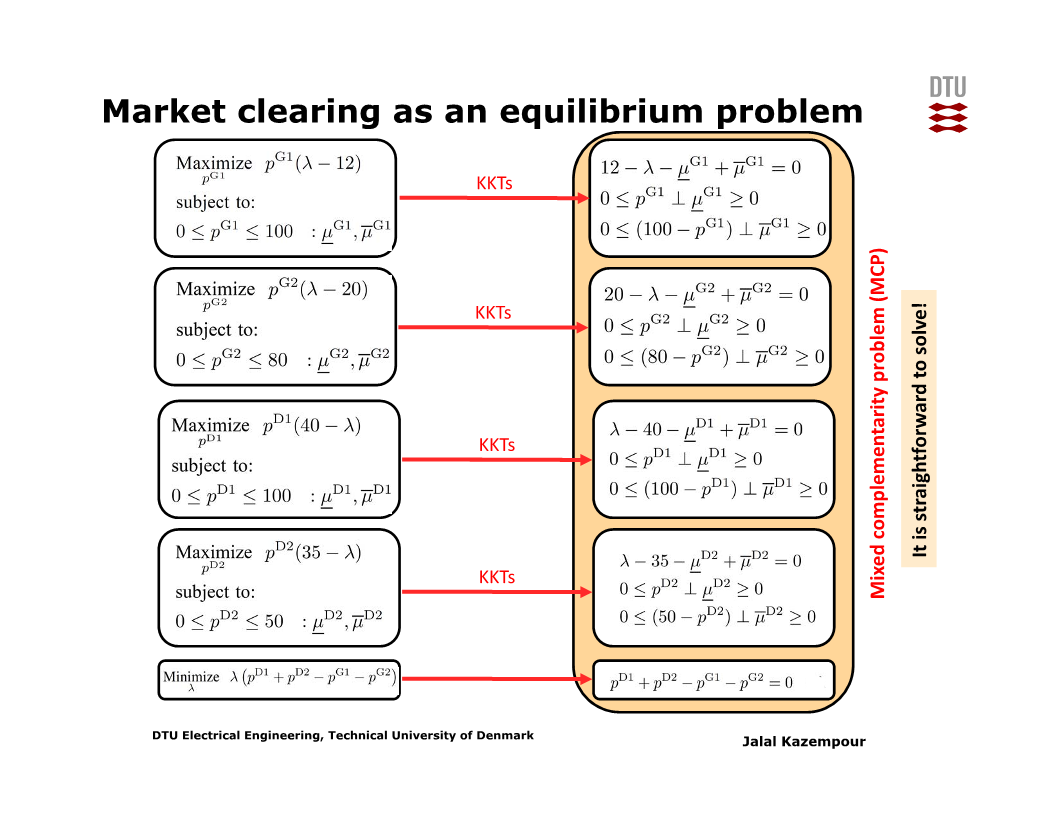
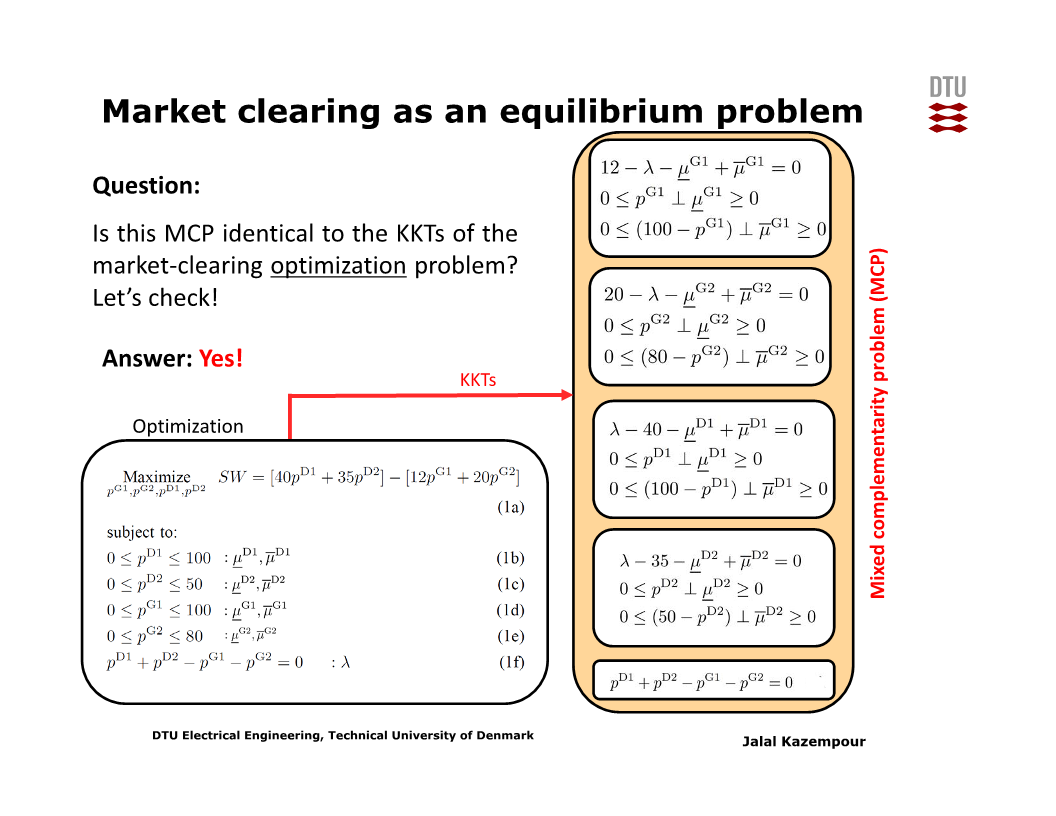
위 두 그림을 보면, 두 문제의 KKT condition이 서로 같으므로 두 문제는 동치이다.
그러므로 market operator가 최적화 문제를 풀면 그 결과는 Nash 균형이다.
일반적으로 각 참가자들의 목적함수를 모두 고려하는 game의 Nash 균형 문제를 푸는 것 보다는 단일 최적화 문제를 푸는 것이 더 쉬우므로, Nash 균형 문제와 최적화 문제 간 동치는 market clearing을 실제로 가능하게 해 주는 좋은 성질이다.
여러 개의 bus가 있어 각 nodal price를 결정하는 경우에도 Nash 균형 문제를 아래와 같이 구성할 수 있다 (DC flow approximation임에 유의).

이 때 두 bus 간 nodal price가 다른 경우, transmission owner는 일종의 공간적 차익거래 (spatial arbitrage) 를 추구한다.
이를테면 bus 1과 bus 2 각각의 nodal price가 $\lambda_1$과 $\lambda_2$이고, 두 bus 간 susceptance가 $B$, 각 bus에서의 voltage angle이 $\theta_1$과 $\theta_2$인 경우, transmission owner의 목적함수는 $(\lambda_2 - \lambda_1) B (\theta_1 - \theta_2)$ 가 되어, $\lambda_2$와 $\lambda_1$ 간에 차이가 있을 경우 (계통혼잡이 있을 경우 nodal price들이 서로 달라짐) 에 공간적 차익에 의한 profit을 벌 수 있다.
이러한 차익 중 일부를 가져갈 권리를 financial transmission rights (FTR) 이라 하며, 실제로 미국에서는 매년 초에 각 송전선 별 FTR을 경매로 판매한다. FTR 구매자 입장에서는 계통혼잡에 의한 nodal price 상승 risk를 hedging할 수 있고, FTR 판매자 입장에서는 연초에 고정수익을 확보할 수 있다.
01) Market clearing as an optimization problem
02) Market clearing as an equilibrium problem
03) Desirable properties of market-clearing mechanisms
04) Market clearing using a cooperative game approach
05) Stochastic market clearing
06) Robust approaches for market clearing
07) Bilevel programming in energy systems
08) Optimization problems with decomposable structure
09) Benders’ decomposition: Theory
10) Benders’ decomposition: Applications
11) Augmented Lagrangian relaxation
12) Variants of ADMM and applications