필자의 ‘선형계획법 기반 분산에너지시스템 최적화’ 시리즈 글에서는, 유효전력의 수요-공급을 고려하는 설비도입계획을 다루었다. 그러나 기 구축된 대규모 발송전시스템의 실제 운영은, 각 발전기 및 bus의 전압/ 무효전력/ 위상도 고려하는 optimal power flow (OPF) 문제를 풀어 이루어진다.


OPF 예시 및 문헌 소개

이를테면 아래 그림의 교류전력망에 대해 OPF 문제를 풀어, 각 발전기의 유효전력과 무효전력 공급량 및 변압기의 전압비와 위상차를 결정해야 한다. 단, 2개 bus에서의 전력부하를 충족하고, 각 bus의 전압 크기와 위상각을 적정 범위 내로 유지하면서, 3개 발전기 연료비의 합을 최소화해야 한다.

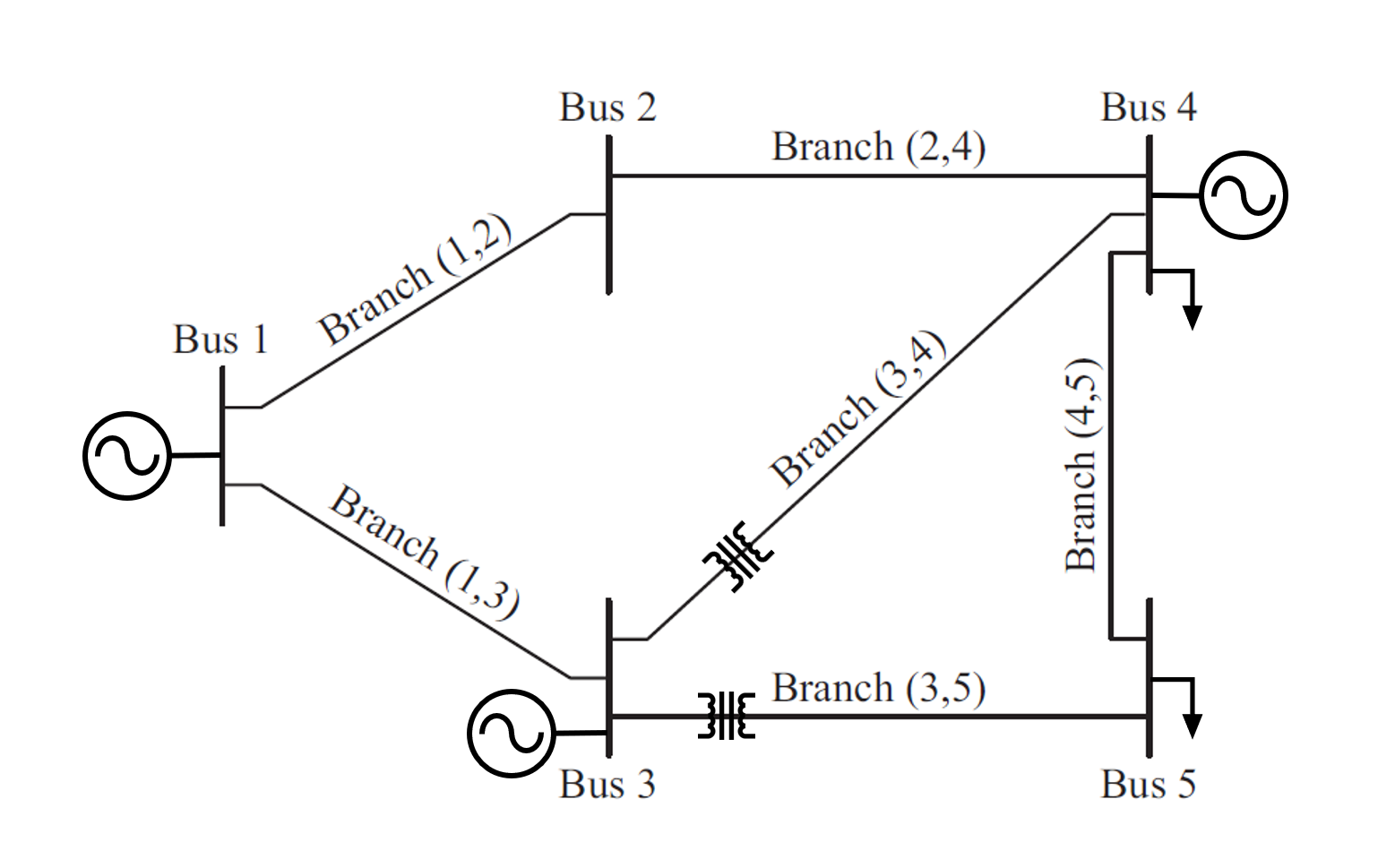optimal power flow 5개의 bus, 3개의 발전기, 2개의 부하로 이루어진 전력망 대상 OPF 문제. 출처: An introduction to optimal power flow: Theory, formulation, and examples

OPF 문제를 제대로 다루려면 전력시스템공학을 제대로 공부해야 한다. 이를테면 필자는 서울대학교 대학원 재학 시절 문승일 교수님의 전력시스템공학 수업에서 Power System Analysis 교재를 공부했었다. 그러나 전력시스템공학의 내용이 방대하고 복잡하여, 본인 연구에 직접 적용하지 않는 한 대부분의 내용을 잊어버리기 쉽다.

다행히, OPF 문제의 기초를 ‘수학적 최적화 문제 구성 및 풀이’ 관점에서 간결하게 설명한 문헌이 있다. An introduction to optimal power flow: Theory, formulation, and examples 이다.

이번 포스팅에서는, 해당 문헌의 OPF 문제 설명 및 numerical example 풀이 코드를 한국어로 재설명한다.


OPF 풀이에 쓰이는 수식들

Bus $1,2,\dots,N$의 복소전압 (즉 범위제약 대상인 전압 크기와 위상각 정보를 담은 복소수) 들을 원소로 하는 복소벡터를 $\tilde{V} = (\tilde{V}_1,\dots,\tilde{V}_N)$ 라 하자.

그리고 bus $i$의 복소전력을 $S_i = P_i + j Q_i$ 라 하고 ($j=\sqrt{-1}$), 유효전력 $P_i = P_i^G - P_i^L$ 를 bus $i$에서 발전되는 유효전력 $P_i^G$와 소비되는 유효전력 $P_i^L$ 간 차이라 하고, 비슷하게 무효전력 $Q_i = Q_i^G - Q_i^L$ 이라 하며, bus $1,2,\dots,N$의 복소전력들을 원소로 하는 복소벡터를 $S = (S_1, \dots, S_N)$ 라 하자.

그러면 복소전류 벡터를 $\tilde{I}$라 할 때 $S = \tilde{V} \circ \tilde{I}^{*}$이다 ($\circ$는 두 벡터 간에 각각 대응하는 원소끼리의 곱, 윗첨자 *는 켤레복소수).

이렇게 되는 이유는, 교류 전압을 $v(t) = V_{max} \text{cos}(wt+\theta_V)$라 하고 교류 전류를 $i(t) = I_{max} cos(wt+\theta_I)$라 할 때 전력이 아래와 같이 계산되고,
$p(t) = v(t)i(t) = 0.5 V_{max}I_{max}[\text{cos}(\theta_V - \theta_I) + \text{cos}(2wt + \theta_V + \theta_I)]$

‘시간에 대한 평균’ 전력은 $0.5 V_{max}I_{max}[\text{cos}(\theta_V - \theta_I)]$이며, 복소전압 $V$와 복소전류 $I$를 각각 $\vert V \vert = V_{max}/\sqrt{2}$, $\vert I \vert = I_{max}/\sqrt{2}$ 가 되게 정의하면 평균적 전력은 아래처럼 계산되기 때문이다.
$P = \text{Re} \vert V \vert e^{j \theta_V} \vert I \vert e^{-j \theta_I} = \text{Re} V I^{*}$

한편 $\tilde{I}$와 $\tilde{V}$ 간에는 $\tilde{I} = \tilde{Y} \tilde{V}$의 관계가 성립하며, 복소행렬 $\tilde{Y}$를 admittance matrix라 한다. 이는 전류가 잘 흐르는 정도를 나타내는 system parameter로 볼 수 있다.

즉, admittance matrix를 $\tilde{Y}$를 구해야 OPF 문제를 풀 수 있다.

특정 두 bus $i$와 $k$를 잇는 전선의 resistance (전력을 소모하는 성분) 을 $R_{ik}$, reactance (코일 등에 의해 교류전력의 위상을 바꾸는 성분) 를 $X_{ik}$라 하면, 해당 전선의 교류전압과 교류전류의 비인 impedence는 $R_{ik} + j X_{ik}$ 이다.

Admittance matrix 계산에서는 impedence의 역수인 series admittance $\tilde{y}_{ik} = (R_{ik} + j X_{ik})^{-1}$를 활용한다.

한편 전선 및 bus 자체에서 전류 누설이 발생할 수 있는데, 이에 관련된 admittance parameter를 shunt admittance라 한다. 두 bus $i$와 $k$를 잇는 전선의 shunt admittance는 $\tilde{y}_{ik}^{Sh}$로, bus $i$ 자체에서의 shunt admittance는 $\tilde{y}_i^{S}$로 표기한다.

서로 다른 두 bus $i$와 $k$를 잇는 전선이 존재할 경우 순서쌍 $(i,k)$가 집합 $\textbf{L}$에 속한다고 하고, $(i,k) \in \textbf{L}$ 이면 $(k,i) \notin \textbf{L}$ 이라고 하자.

그러면, admittance matrix $\tilde{Y}$의 각 성분 $\tilde{Y}_{ik}$는 아래와 같이 계산된다.

\begin{align} \tilde{Y}_{ii} = \tilde{y}_i^{S} +\sum_{k:(i,k) \in \textbf{L}} \frac{1}{\vert a_{ik} \vert^2} (\tilde{y}_{ik} + \frac{1}{2} \tilde{y}_{ik}^{Sh})+ \sum_{k:(k,i) \in \textbf{L}} (\tilde{y}_{ki} + \frac{1}{2} \tilde{y}_{ki}^{Sh}) \notag \end{align} \begin{align} \tilde{Y}_{ik} = - \sum_{k:(i,k) \in \textbf{L}} \frac{1}{ a_{ik}^{*}} \tilde{y}_{ik} - \sum_{k:(k,i) \in \textbf{L}} \frac{1}{ a_{ki}} \tilde{y}_{ki} \quad (i \ne k) \notag \end{align}

여기서 $a_{ik}=T_{ik} e^{j \phi_{ik}}$는 변압을 의미한다. 변압기가 따로 없으면 1이고, 변압기가 있으면 $T_{ik}$는 전압비, $\phi_{ik}$는 변압기 전후 위상차이다.

그리고 $\tilde{Y}_{ik} = G_{ik} + j B_{ik}$라 하고 ($G_{ik}$를 conductance, $B_{ik}$를 susceptance라 함), 복소전압 $\tilde{V}_i = V_i e^{j \delta_i}$로 나타낼 때, bus $i$에서의 복소전력 $S_i = P_i + j Q_i$를 구하는 식은 아래와 같다.

\begin{align} P_i = V_i \sum_{k=1}^N V_k [G_{ik} \text{cos}(\delta_i - \delta_k) + B_{ik} \text{sin} (\delta_i - \delta_k)] \notag \end{align} \begin{align} Q_i = V_i \sum_{k=1}^N V_k [G_{ik} \text{sin}(\delta_i - \delta_k) - B_{ik} \text{cos} (\delta_i - \delta_k)] \notag \end{align}

이를 power flow equation이라 한다.

최적화 문제 코딩을 위해 power flow equation을 우변이 0인 형태로 다시 쓰고 $P_i = P_i^G - P_i^L$, $Q_i = Q_i^G - Q_i^L$ 를 대입하면 아래와 같다.

\begin{align} P_i^L - P_i^G + V_i \sum_{k=1}^N V_k [G_{ik} \text{cos}(\delta_i - \delta_k) + B_{ik} \text{sin} (\delta_i - \delta_k)] = 0 \notag \end{align} \begin{align} Q_i^L - Q_i^G + V_i \sum_{k=1}^N V_k [G_{ik} \text{sin}(\delta_i - \delta_k) - B_{ik} \text{cos} (\delta_i - \delta_k)] = 0 \notag \end{align}

이제 OPF 문제를 구성한다. OPF로 결정해야 할 변수들은 아래와 같다.

1) 각 bus의 전압의 크기와 위상각
2) Bus 1,3,4의 발전기의 유효전력과 무효전력
3) Bus 3과 4 간 변압기의 위상차 (전압비는 1:1로 고정임)
4) Bus 3과 5 간 변압기의 전압비 (위상차는 0으로 고정임)

등호 제약조건은 위 power flow equation이고, 부등호 제약조건은 각 bus 별 전압과 위상각의 적정 범위, 각 발전기 별 유효전력과 무효전력 출력의 상하한, 변압기의 전압비와 위상차의 상하한이다. 목적함수는 각 발전기 별 연료비의 합으로, 각 발전기 별 유효전력 출력의 이차함수로 주어진다.

주어지는 데이터는 각 전선 별 resistance/ reactance/ shunt admittance, 각 bus 별 shunt admittance, 각 부하의 요구 유효전력과 무효전력 값, bus 별 전압의 상하한 값, 발전기의 유효전력출력과 무효전력출력의 상하한 값이다.

이 문헌에서 소개하는 OPF 문제는 ‘한 시점에 대한’ 문제임에 주의한다. 해당 OPF 문제는 여러 시점들에 걸친 스케줄링 문제가 아니다.


예제 풀이용 python 코드

필요한 라이브러리는 Numpy, 그리고 비선형 최적화 문제의 제약조건 구현과 풀이에 필요한 Scipy.optimize의 NonlinearConstraint와 minimize 모듈이다.

import numpy as np
from scipy.optimize import NonlinearConstraint, minimize

최적화 문제를 코드로 풀 때는 값을 결정할 변수들이 단일 벡터 $x$의 원소인데, $x$의 각 원소의 인덱스를 아래처럼 물리량의 이름을 따서 부여하면 코드를 읽기 쉽고 실수도 줄어든다.

v_bus = np.arange(0,5) # 인덱스 0~4는 각 bus의 전압크기
del_bus = np.arange(5,10,1) # 인덱스 5~9는 각 bus의 전압위상각
p_bus = np.arange(10,15,1) # 인덱스 10~14는 각 bus 내 발전기의 유효전력 (발전기가 없으면 0)
q_bus = np.arange(15,20,1) # 인덱스 15~19는 각 bus 내 발전기의 무효전력 (발전기가 없으면 0)
phi_transf = 20 # 인덱스 20은 bus 3과 4 간 변압기의 위상차
mag_transf = 21 # 인덱스 21은 bus 3과 5 간 변압기의 전압비
# 이를테면 # x[v_bus[0]] 은 1번 bus의 전압크기를, x[del_bus[1]] 은 2번 bus의 전압위상각을 의미

주어진 시스템 데이터인 각 전선 별 series admittance와 shunt admittance, 각 bus 별 shunt admittance, 각 부하의 유효전력 및 무효전력 요구치를 기재한다. 이 때 dtype=complex 로 두어 복소수로 쓴다.
또한 모든 물리량은 per unit 단위법으로 쓰였음에 주의한다.

n_bus = 5

y_series = np.zeros((n_bus,n_bus),dtype=complex) # 각 전선의 series admittance
y_sh_branch = np.zeros((n_bus,n_bus),dtype=complex) # 각 전선의 shunt admittance
y_sh_bus = np.zeros((n_bus),dtype=complex) # 각 bus의 shunt admittance

y_series[0,1]= 1/(0+0.3j) # bus 1과 2를 잇는 전선의 series admittance
y_series[0,2] = 1/(0.023+0.145j) # (i,k)가 L의 원소일 때 (k,i)는 L의 원소가 아닌 것과 같은 맥락으로 y_series[2,0] 은 설정하지 않음에 주의
y_series[1,3] = 1/(0.006+0.032j)
y_series[2,3] = 1/(0.02+0.26j)
y_series[2,4] = 1/(0+0.32j)
y_series[3,4] = 1/(0+0.5j)
y_sh_branch[0,2] = (0+0.04j) # bus 1과 3을 잇는 전선의 shunt admittance
y_sh_branch[1,3] = (0+0.01j)
y_sh_bus[1] = 0+0.3j # bus 2의 shunt admittance
y_sh_bus[2] = 0.05+0j
    
load_bus = np.array([0+0j, 0+0j, 0+0j, 0.9+0.4j, 0.239+0.129j]) # bus 4와 5의 전력 부하

비선형 제약조건인 power flow equation을 $x$의 사용자 정의 함수로 정의한다. 먼저 admittance matrix $\tilde{Y}$를 계산하고, 그 뒤에 $P_i$와 $Q_i$에 대한 등식을 기재한다. 이 문제에서는 변압기가 있으므로 $\tilde{Y}$ 계산 내 $a_{ik}$가 최적화로 값을 구할 변수의 함수이기 때문에, $\tilde{Y}$ 계산이 사용자 정의 함수 내에서 이루어져야 함에 주의한다.

def nonlconfun(x): # 비선형 제약조건의 좌변을 변수들의 함수로 계산

    a_tx = np.ones((n_bus,n_bus),dtype=complex) # 변압비와 위상차 phasor        
    a_tx[2,3] = 1*np.exp(1j*x[phi_transf]) # bus 3과 4 간 변압기의 위상차는 최적화로 도출 필요
    a_tx[2,4] = x[mag_transf]*np.exp(1j*0) # bus 3과 5 간 변압기의 전압비는 최적화로 도출 필요
    
    y_full = np.zeros((n_bus,n_bus),dtype=complex) # admittance matrix
    
    for fr in range(n_bus):
        y_full[fr,fr] = y_sh_bus[fr] # Y_ii
        for to in range(n_bus):
            y_full[fr,fr] = y_full[fr,fr] + (y_series[fr,to] + 0.5*y_sh_branch[fr,to])/(np.abs(a_tx[fr,to])**2) + (y_series[to,fr] + 0.5*y_sh_branch[to,fr])
            if to != fr: # Y_ik
                y_full[fr,to] = y_full[fr,to] - y_series[fr,to]/np.conjugate(a_tx[fr,to]) - y_series[to,fr]/a_tx[to,fr] 
    
    ceq = np.zeros((n_bus*2)) # 제약조건의 좌변 값을 담을 벡터
    
    for m in range(n_bus): # Power flow equation
        ceq[m] = np.real(load_bus[m]) - x[p_bus[m]] # 인덱스 0, 1, ..., m-1은 유효전력
        ceq[n_bus+m] = np.imag(load_bus[m]) - x[q_bus[m]] # 인덱스 m, m+1, ..., 2m-1은 무효전력
        for k in range(n_bus):
            ceq[m] = ceq[m] + x[v_bus[m]]*x[v_bus[k]]*(np.real(y_full[m,k])*np.cos(x[del_bus[m]]-x[del_bus[k]]) + np.imag(y_full[m,k])*np.sin(x[del_bus[m]]-x[del_bus[k]])) # real power at bus m
            ceq[n_bus+m] = ceq[n_bus+m] + x[v_bus[m]]*x[v_bus[k]]*(np.real(y_full[m,k])*np.sin(x[del_bus[m]]-x[del_bus[k]]) - np.imag(y_full[m,k])*np.cos(x[del_bus[m]]-x[del_bus[k]])) # reactive power at bus m
    
    return ceq # 제약조건의 좌변 값을 반환

목적함수를 $x$의 사용자 정의 함수로 정의한다. 목적함수인 발전기의 연료비의 합은 각 발전기 별 유효전력의 이차함수이다.

def objfun(x):
    cost = 0.35*x[p_bus[0]] + 0.2*x[p_bus[2]] + 0.4*x[p_bus[2]]**2 + 0.3*x[p_bus[3]] + 0.5*x[p_bus[3]]**2
    return cost

각 변수의 상하한을 설정하되, 1번 bus를 slack bus로 생각하고 설정한다. 초기값은 변수별 상하한 간 중간값으로 설정한다.

bounds = [(1,1), # Bus 1은 Slack Bus이므로 전압크기 1로 고정
        (0.95,1.05),
        (0.95,1.05),
        (0.95,1.05),
        (0.95,1.05),
        (0,0), # Bus 1은 Slack Bus이므로 위상각 0으로 고정
        (-np.pi,np.pi), # 위상각의 단위가 radian임에 주의
        (-np.pi,np.pi),
        (-np.pi,np.pi),
        (-np.pi,np.pi),
        (-10,10), # Bus 1은 unrestricted
        (0,0), # Bus 2에는 발전기 없어 0으로 고정
        (0.1,0.4),
        (0.05,0.4),
        (0,0), # Bus 5에는 발전기 없어 0으로 고정
        (-10,10), # Bus 1은 unrestricted
        (0,0), # Bus 2에는 발전기 없어 0으로 고정
        (-0.2,0.2),
        (-0.2,0.2),
        (0,0), # Bus 5에는 발전기 없어 0으로 고정
        (-np.pi/6,np.pi/6),
        (0.95,1.05)]

initialpoint = (np.array(bounds)[:,0]+np.array(bounds)[:,1])/2

Power flow equation은 복잡한 비선형 방정식이다. 그러므로 일반적인 비선형 문제를 푸는 solver를 사용해야 한다. 여기서는 Scipy.optimize의 NonlinearConstraint와 minimize 모듈을 이용한다.

nonlcon = NonlinearConstraint(nonlconfun, np.zeros((n_bus*2,)), np.zeros((n_bus*2,))) # 모든 변수들에 대해 우변의 하한과 상한이 모두 0, 즉 우변이 0인 등호조건

sol = minimize(objfun,initialpoint,bounds=bounds,constraints=nonlcon) # solver로 OPF 문제 풀기

solution = np.multiply(sol.x, # 전압 위상각의 단위를 radian에서 degree로 변환
                       np.array([1,1,1,1,1,180/np.pi,180/np.pi,180/np.pi,180/np.pi,180/np.pi,1,1,1,1,1,1,1,1,1,1,180/np.pi,1]))
print(solution[v_bus[1]],solution[v_bus[2]],solution[v_bus[3]],solution[v_bus[4]],"\n",
      solution[del_bus[1]],solution[del_bus[2]],solution[del_bus[3]],solution[del_bus[4]],"\n",
      solution[p_bus[0]],solution[p_bus[2]],solution[p_bus[3]],"\n",
      solution[q_bus[0]],solution[q_bus[2]],solution[q_bus[3]],"\n",
      solution[phi_transf],solution[mag_transf])

코드를 실행하면, 논문에서 제시한 답과 같은 결과를 얻는다.

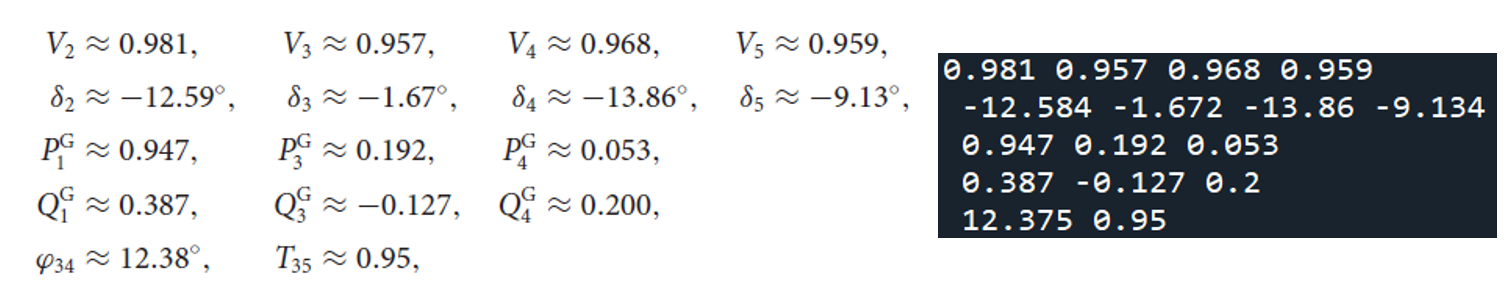solution of OPF OPF 문제의 해답 (좌측은 논문 내용, 우측은 필자가 작성한 코드의 마지막 print문 결과).

전체 코드는 필자의 GitHub Repo에 업로드하였다.

해당 numerical example의 한계점은, 각 전선의 전류량 상한을 고려하지 않았다는 점이다. 실제로는 전선에 전류가 지나치게 많이 흐르면 전선이 열손상을 입기 때문에, 전선별로 thermal limit이 있다. 필요 시 전선 별 thermal limit을 추가적인 비선형 부등호 제약조건으로 반영해야 할 것으로 보인다.