시간별 태양광 발전량 계산 모델 수식 설명
태양광 패널을 포함하는 마이크로그리드의 경제성 분석을 위해서는 시간별 태양광 발전량을 계산해야 한다. 필자가 국내 케이스의 계산에 사용하는 데이터로는 기상청에서 제공하는 시간별 일사량이 있다. 즉, 시간별 일사량 데이터를 태양광 발전량으로 변환해야 한다.
시간별 일사량 데이터를 태양광 발전량으로 변환한 결과만 얻고 싶다면, 미국의 National Renewable Energy Laboratory (NREL)에서 개발한 재생에너지시스템 경제성평가 tool인 System Advison Model (SAM)을 사용하면 된다.
SAM으로 시간별 태양광 발전량을 계산하기 위한 ‘프로그램 사용’ 방법은 필자의 NAVER 블로그 포스트에서 설명한 바 있다.
그러나 SAM 사용 시 사용자가 매 case마다 수동으로 변환해야 한다. 만약 어떤 커스터마이징된 데이터 파이프라인이 일사량을 받고 자동으로 태양광 발전량으로 변환해 주기를 원한다면, SAM을 사용할 수 없다. 대신 태양광 발전량 계산 모델을 직접 코딩해서 포함시켜야 한다.
이 포스트에서는, 기상청에서 제공하는 시간별 일사량으로 시간별/ 위도별/ 패널 각도별 태양광 발전량을 계산하는 수리모델을 설명한다. 참고한 자료들은 아래와 같다.
1) “Hybrid hydrogen systems”의 Chapter 2 “Renewable Energy Sources and Energy Conversion Devices”
2) A comprehensive solar angles simulation and calculation using Matlab
3) Estimation of the diffuse radiation fraction for hourly, daily and monthly-average global radiation
임의의 위치/ 날짜/ 시간에 태양으로부터 직달하는 일사량 계산
먼저 지구 대기권 경계에 직달하는 일사량의 연중 평균값을 global solar constant $G_{sc}$ 라 하며, 약 $1,367 \text{W}/m^2$이다.
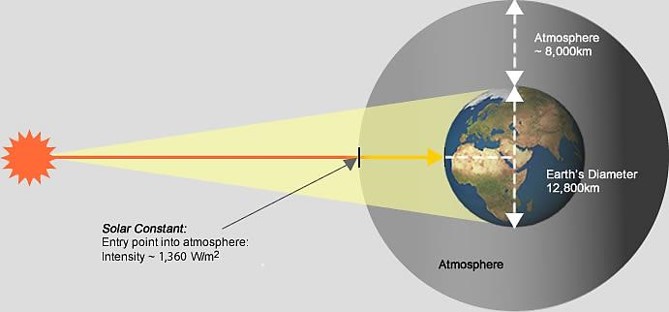 Global solar constant. (출처: https://www.greenrhinoenergy.com/solar/radiation/extraterrestrial.php)
Global solar constant. (출처: https://www.greenrhinoenergy.com/solar/radiation/extraterrestrial.php)
실제 각 날짜별로 지구 대기권 경계에 직달하는 실제 일사량 $G_{en}$은 지구 공전에 의해 달라진다. $G_{en}$은 $n=1,2,\dots,365$이며 1월 1일에 $n=1$이라 할 때 아래와 같다.
\begin{align} G_{en} = G_{sc}\left(1 + 0.033 \text{cos} \frac{360n}{365} \right) \notag \end{align}
실제로는 시간 및 위도에 따라서도 일사량이 다르다. 위도(latitude)를 $\phi$, 시간에 대응하는 각도인 hour angle (정오 즉 남향일 때 0, 오후에 플러스, 오전에 마이너스, 1시간당 15도 변화) 을 $\omega$, 직달일사량과 지구 적도 간 각도인 declination angle 을 $\delta$라 할 때, 해당 날짜/ 위도/ 시간에 도달하는 일사량은 아래와 같다. (각 변수들의 구체적 의미는 식 아래 그림들 참고)
\begin{align} G_{0} = G_{sc}\left(1 + 0.033 \text{cos} \frac{360n}{365} \right) \left(\text{cos}\phi \text{cos}\delta \text{cos}\omega + \text{sin}\phi \text{sin}\delta \right) \quad \text{where} \,\, \delta = 23.45^o \text{sin} \left[\frac{360^o}{365}(284+n) \right] \notag \end{align}
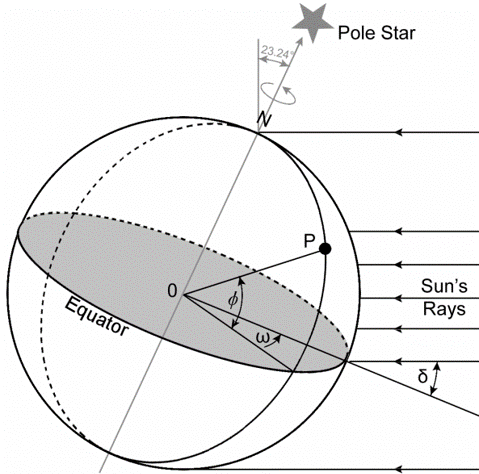 위도, hour angle, declination angle 도식도. (출처: Estimation of Hourly, Daily and Monthly Global Solar Radiation on Inclined Surfaces: Models Re-Visited)
위도, hour angle, declination angle 도식도. (출처: Estimation of Hourly, Daily and Monthly Global Solar Radiation on Inclined Surfaces: Models Re-Visited)
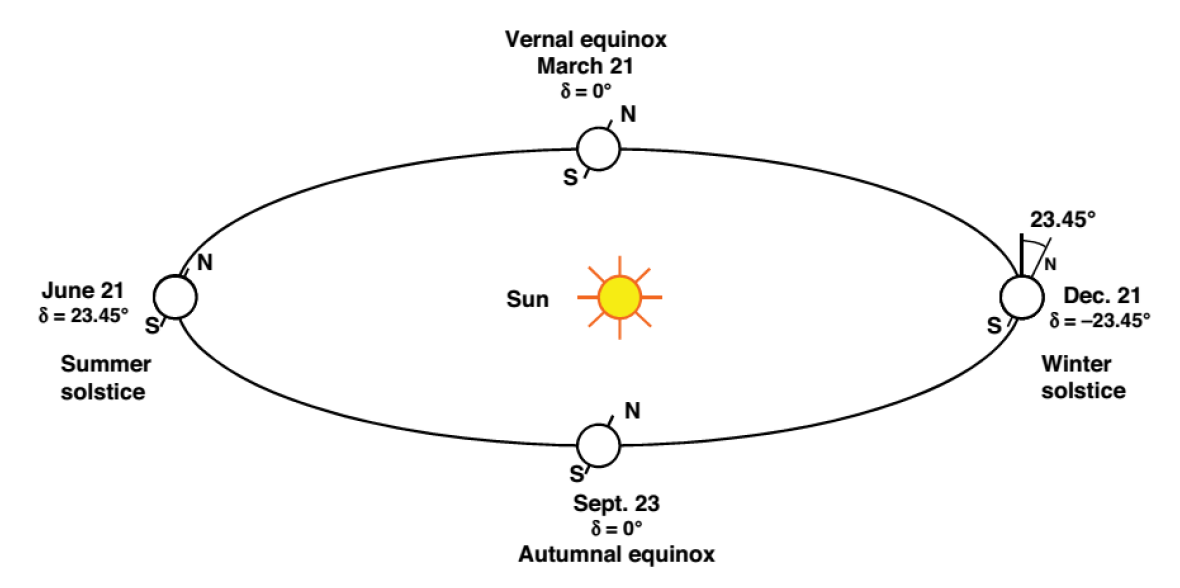 Declination angle의 연중 변화. (출처: A comprehensive solar angles simulation and calculation using Matlab)
Declination angle의 연중 변화. (출처: A comprehensive solar angles simulation and calculation using Matlab)
실제 에너지시스템 최적화 문제를 풀 때 필요한 수치는 ‘$k$시부터 $k+1$시까지 도달한 총 에너지’ 이다. 이는 $k$시와 $k+1$시의 hour angle을 각각 $w_1$과 $w_2$라 할 때, 적분에 의해 아래와 같이 계산된다 (단위는 Wh).
\begin{align} I_o = \int_{w_1}^{w_2} G_o dw = \frac{12}{\pi} G_{en} \left[ \text{cos} \phi \text{cos} \delta (\text{sin} \omega_2 - \text{sin} \omega_1) + \frac{\pi (\omega_2 - \omega_1)}{180} \text{sin} \phi \text{sin} \delta \right] \notag \end{align}
임의의 각도로 설치된 패널과 태양 광선 간 각도 계산
지금까지의 논의는 모두 수평면에 도달하는 일사량에 대한 것이었다. 그러나 태양광 패널은 지면으로부터 일정 각도로 기울어져 설치되며, 대부분의 경우 정남향을 향하게 설치되지만 그렇지 않은 경우도 꽤 있다.
지상으로부터 $\beta$만큼의 경사각으로 기울어져 있고 남향을 기준으로 $\gamma$만큼의 각도로 틀어져 있는 (서향이면 플러스, 동향이면 마이너스) 패널의 법선과 그 평면에 직달하는 일사량 간의 각도를 $\theta$ (angle of incidence) 라 하자.
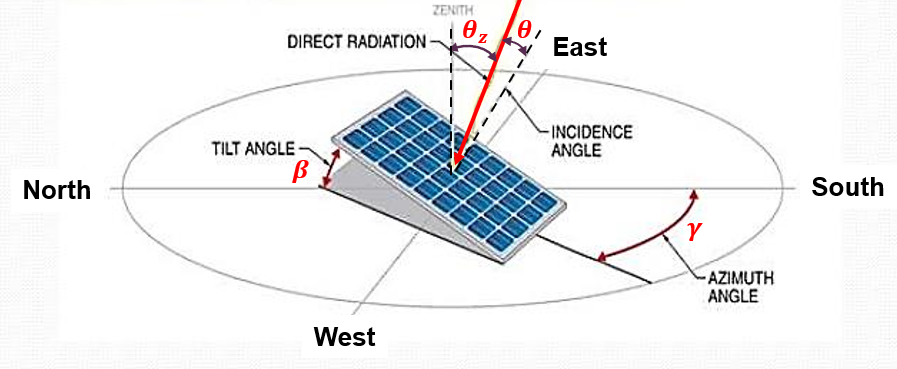 태양광 패널의 설치각 및 angle of incidence. (출처: Optimal design and analysis of grid-connected photovoltaic under different tracking systems using HOMER)
태양광 패널의 설치각 및 angle of incidence. (출처: Optimal design and analysis of grid-connected photovoltaic under different tracking systems using HOMER)
이 때 $\theta$는 아래와 같이 계산된다.
\begin{align} \text{cos} \theta = \text{sin} \delta \text{sin} \phi \text{cos} \beta - \text{sin} \delta \text{cos} \phi \text{sin} \beta \text{cos} \gamma + \text{cos} \delta \text{cos} \phi \text{cos} \beta \text{cos} \omega + \text{cos} \delta \text{sin} \phi \text{sin} \beta \text{cos} \gamma \text{cos} \omega + \text{cos} \delta \text{sin} \beta \text{sin} \gamma \text{sin} \omega \notag \end{align}
위 식에서 $\beta=0$이면 지면 기준 ‘수평’면과 일사량 간의 각도 $\theta_z$ (zenith angle) 이다.
\begin{align} \text{cos} \theta_z = \text{cos} \phi \text{cos} \delta \text{cos} \omega + \text{sin} \phi \text{sin} \delta \notag \end{align}
잘 보면, $G_{0}$ 계산식에 $\text{cos} \theta_z$가 포함되어 있다.
대기의 효과를 고려한 유효 일사량 계산
$I_o$는 태양광이 대기를 뚫고 지면에 도달하는 과정에서 대기의 영향을 고려하지 않은 값이다. 실제로는 대기에서 산란이 발생하므로, 이 효과를 고려해야 한다.
대기 효과를 고려해 최종적으로 수평 지표면에 도달하는 일사량을 수평면전일사량 (Global Horizontal Irradiance, GHI) $I$라 하며, 기상청 종관기상관측자료에서 제공하는 일사량 값이 GHI이다.
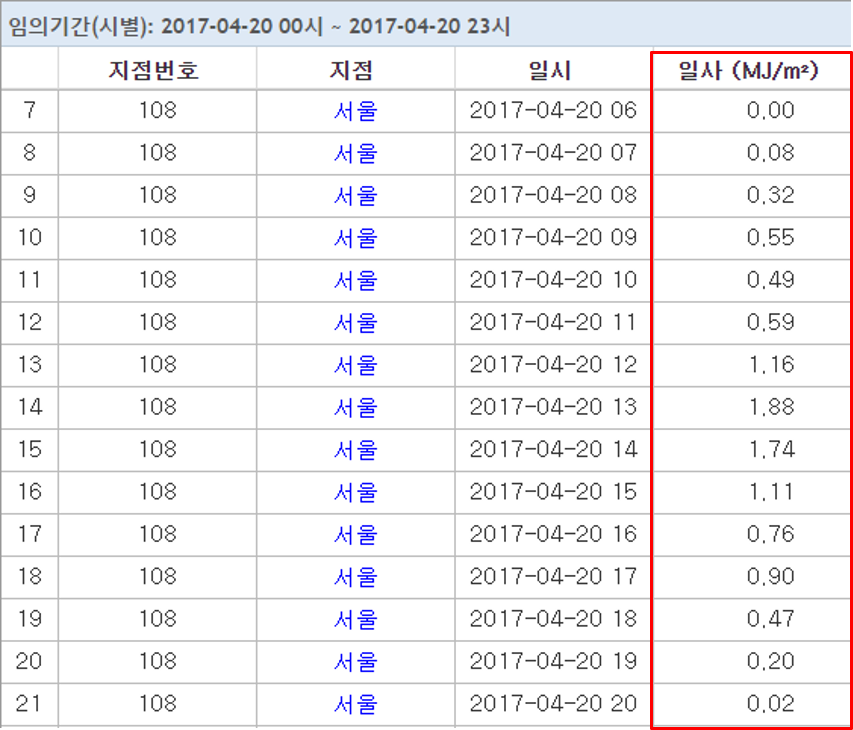 기상청 종관기상관측자료에서 제공하는 시간별 GHI 데이터. 단위가 MJ/$m^2$임에 주의 (필자는 태양광 패널 성능곡선 단위가 W임에 착안해 1000을 곱한 후 3.6으로 나눈 값을 사용한다).
기상청 종관기상관측자료에서 제공하는 시간별 GHI 데이터. 단위가 MJ/$m^2$임에 주의 (필자는 태양광 패널 성능곡선 단위가 W임에 착안해 1000을 곱한 후 3.6으로 나눈 값을 사용한다).
지표면에 도달하는 일사량은 두 가지 성분으로 나눌 수 있다. 하나는 태양에서 지표면까지 직달하는 beam (direct) radiation $I_b$이고, 다른 하나는 대기 중에서 산란되어 해당 지표면에 도달하는 diffuse radiation $I_d$이다.
한편 지표면에 도달한 태양 에너지의 일부는 우주로 반사되어 나가며, 반사되는 에너지의 비율을 albedo라 한다. Albedo의 연중 평균값은 대략 $\rho_g \approx 0.35$ 이다.
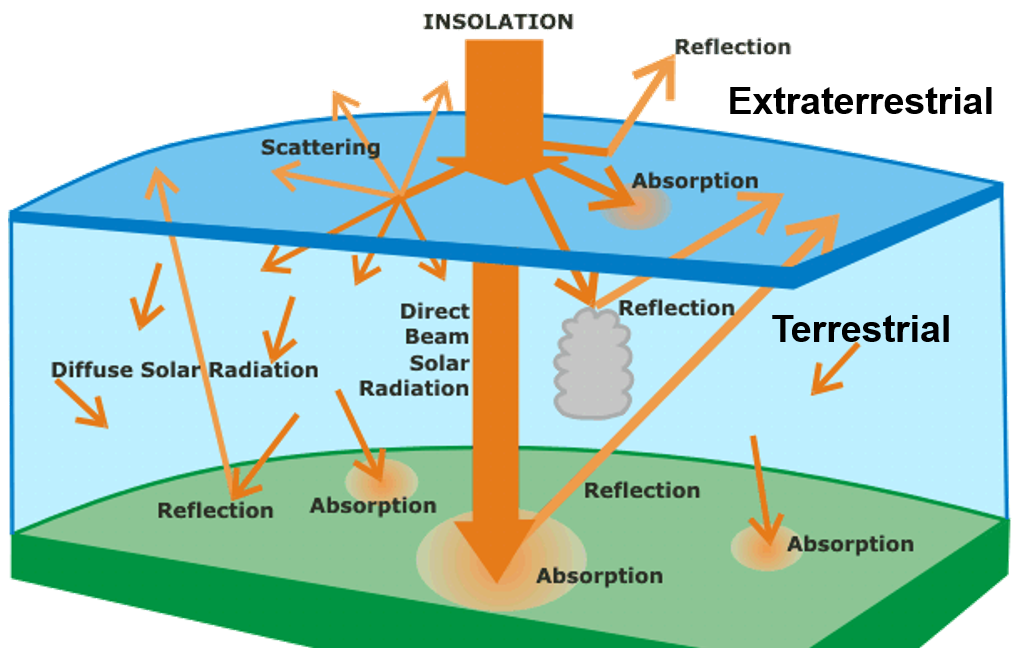 Beam radiation과 diffuse radiation의 concept. (출처: https://faculty.uml.edu/Nelson_Eby/ENVI.5720/Instructor%20Pdfs/Chapt%209%20-%20Solar%20Power.pdf)
Beam radiation과 diffuse radiation의 concept. (출처: https://faculty.uml.edu/Nelson_Eby/ENVI.5720/Instructor%20Pdfs/Chapt%209%20-%20Solar%20Power.pdf)
만약 $I=I_b + I_d$ 뿐 아니라 $I_b$와 $I_d$ 각각의 값을 안다면, 아래의 HDKR 모델 (Hay, Davies, Klucher, Reindl) 을 이용해 실제 태양광 발전량 계산의 기준이 되는 일사량 $I_T$ 를 계산할 수 있다.
\begin{align} I_T = \left(I_b + \frac{I_d I_b}{I_o}\right) \frac{\text{cos} \theta}{\text{cos} \theta_z} + I_d \left(1- \frac{I_b}{I_o}\right) \left(\frac{1+\text{cos}\beta}{2}\right) \left[ 1 + \sqrt{\frac{I_b}{I}} \text{sin}^3 (\frac{\beta}{2}) \right] + I \rho_g \left(\frac{1-\text{cos}\beta}{2}\right) \notag \end{align}
$I_b$와 $I_d$의 값들을 추정하는 방법으로 Erbs’ correlation이 있다. 이는 $I_d/I$를 $K_T=I/I_o$로 정의되는 clearness index의 함수로 근사하는 correlation으로, $I$를 알면 $I_d$를 추정하고 이로부터 $I_b$ 또한 추정할 수 있다. 구체적 식은 아래와 같다.
\begin{align} I_d/I = \begin{array}{rl} 1 - 0.09 K_T & \text{if } K_T \leq 0.22, \newline 0.9511 - 0.1604 K_T + 4.388 K_T^2 - 16.638 K_T^3 + 12.336 K_T^4 & \text{if } 0.22 \leq K_T \leq 0.80, \newline 0.165 & \text{if } 0.80 < K_T \end{array} \notag \end{align}
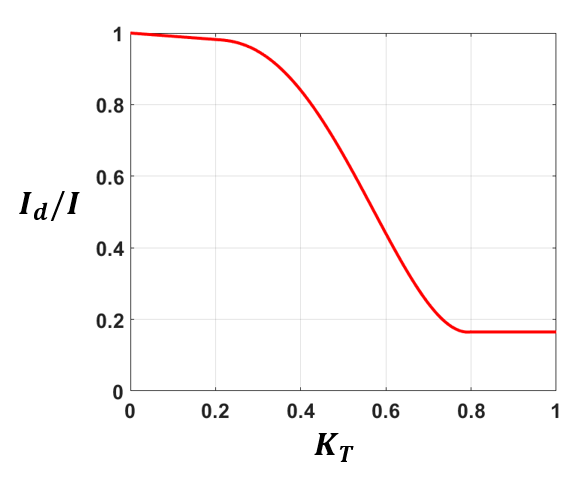 Clearness index와 $I_d/I$ 간 관계 (Erbs’ correlation)
Clearness index와 $I_d/I$ 간 관계 (Erbs’ correlation)
일사량을 태양광 패널 출력으로 변환
패널에 도달하는 일사량 $I_T$를 태양광 발전량 $P_{pv}$로 변환하기 위해선 태양광 패널의 성능 곡선이 필요하다. 일반적으로 아래 그림처럼 nominal efficiency (세로축이 1.00일 때의 변환효율, 이를테면 15.1퍼센트) 대비 상대적인 값이 $I_T$의 함수로 주어진다.
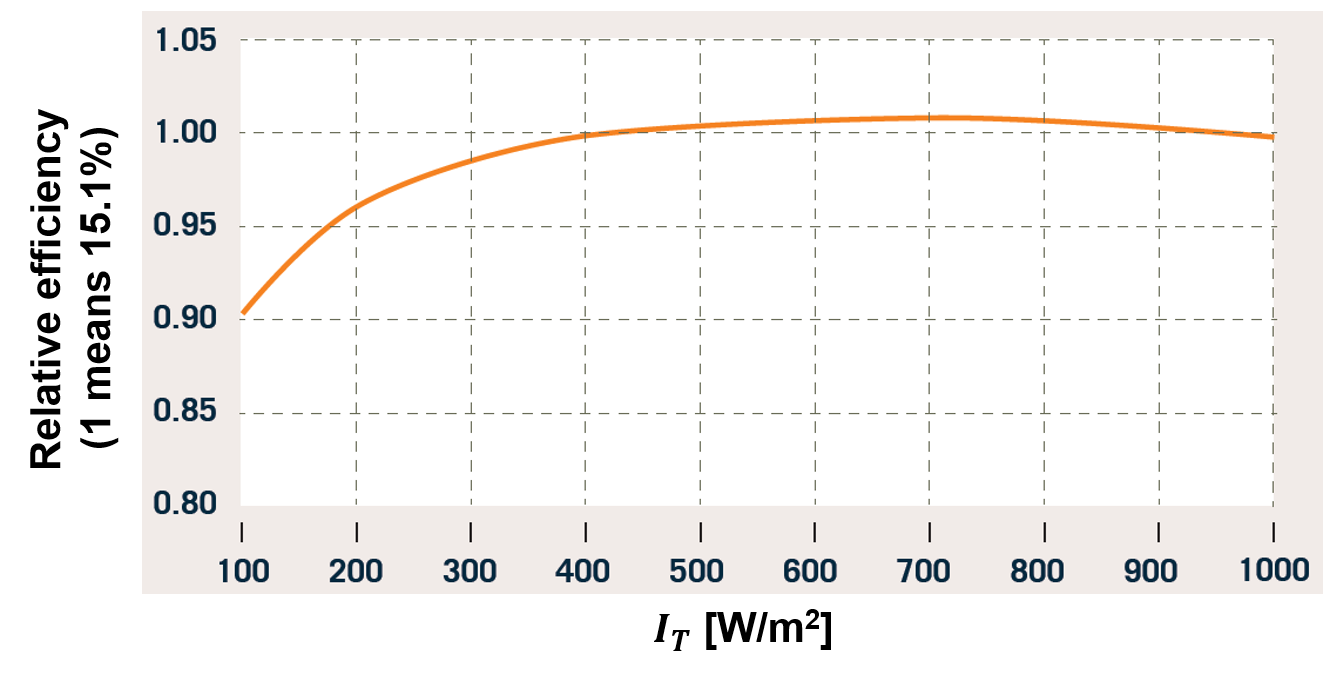 태양광 패널의 성능곡선.
태양광 패널의 성능곡선.
위 그림의 가로축의 단위는 W이지만 $I_T$의 단위는 Wh이다. 그러므로 편의상, 해당 1시간 동안 일사량의 세기는 일정하다고 가정하여, $I_T$의 값을 위 성능곡선에 대입해 $P_{pv}$를 계산한다.
계산 모델 검증
아래 그림은, 모 지역의 정수시설에 설치된 태양광 패널의 특정 연도의 5월 실제 발전량 기록 (파란색) 과, 해당 지점으로부터 약 16km 떨어진 기상대에서 측정된 GHI와 이 포스팅에서 소개한 HDKR 모델로 계산된 태양광 발전량 추정치 (빨간색) 를 비교한 결과이다.
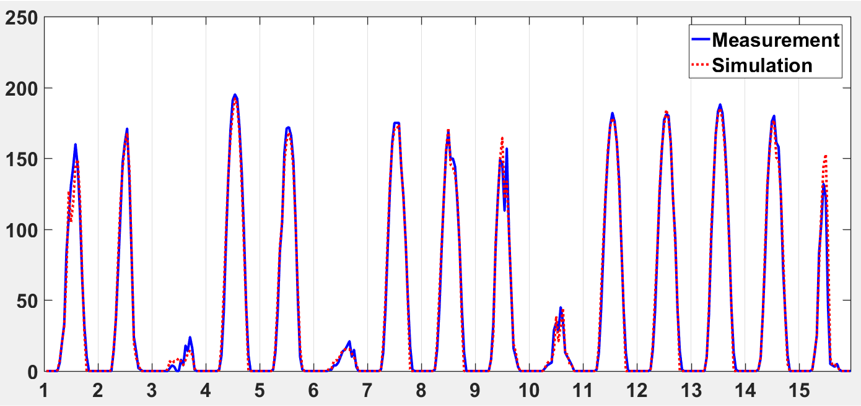
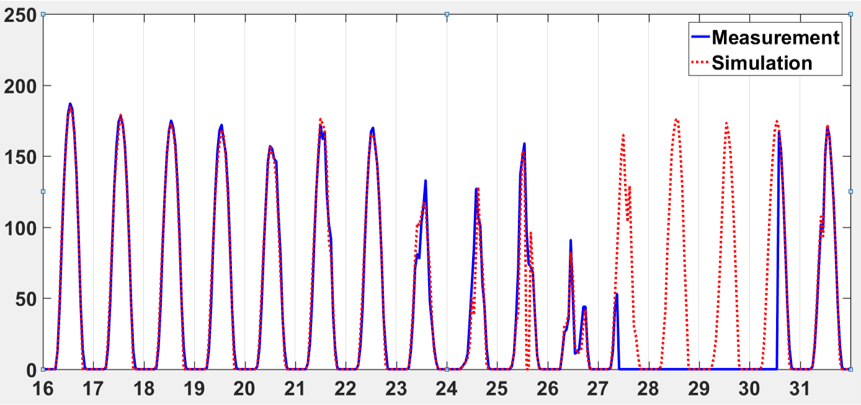 태양광 패널의 실제 발전량 기록 (파랑) 과 모델 기반 계산 결과 (빨강) 비교. 세로축 단위는 kW.
태양광 패널의 실제 발전량 기록 (파랑) 과 모델 기반 계산 결과 (빨강) 비교. 세로축 단위는 kW.
모델이 실제 발전량과 충분히 유사한 값을 계산해줌을 볼 수 있다. 참고로 27~30일은 시설 유지보수가 있었던 것으로 추정된다.