전기차 및 충전 인프라 규모가 증가할수록 전력계통에 걸리는 부하가 증가한다. 그러므로 향후 발전/ 송전/ 배전 (특히 배전단) 설비 및 스케줄링 계획 수립을 위해, 전기차 충전으로 인한 시간별 부하 증가를 정확히 예측할 필요가 있다.

이를테면 McKinsey에서는 150세대의 주거지역 배전단에서 가정 내 전기차 비중이 25%가 되면 아래 그림과 같이 모든 시간의 전기부하가 증가하며, 특히 최대부하는 약 30% 증가할 것으로 예상했다.

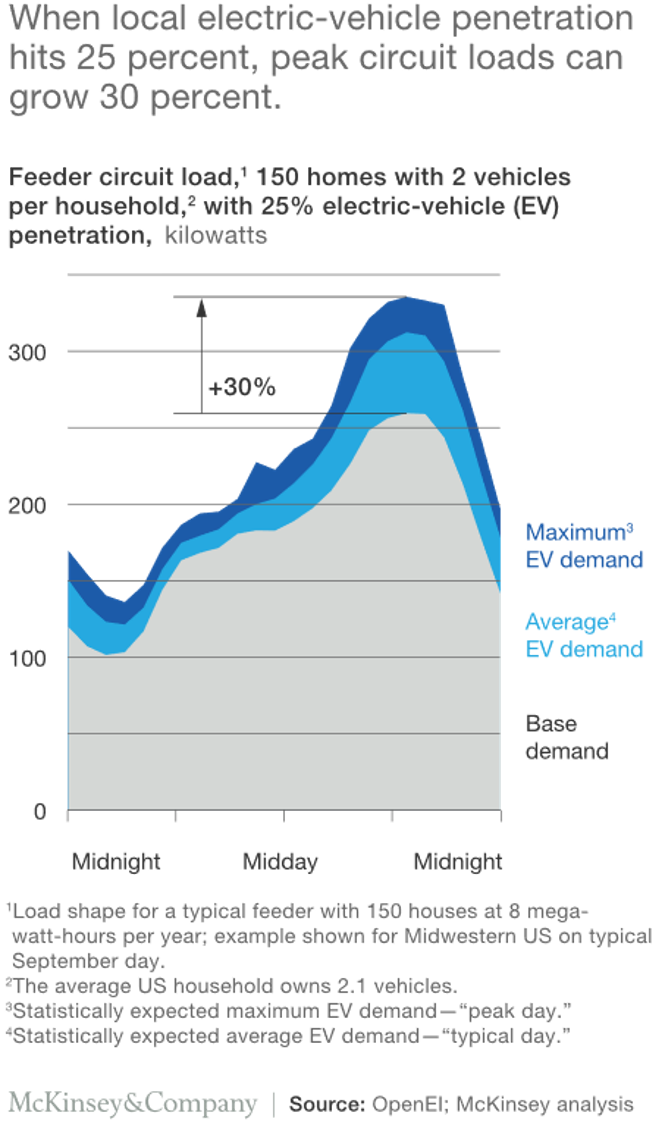impact_ev 전기차 증가로 인한 시간별 부하 증가 예상. (출처: 위 링크의 McKinsey 웹페이지)

또한 최근에는 수 kW급의 저속충전 뿐 아니라 100kW 이상의 고속충전 인프라가 확산되고 있으므로, 전기차 충전이 짧은 시간 내에 특정 배전 계통에 큰 부담을 줄 가능성도 고려해야 한다.

(그나마 한국에서는 최근 전기차 충전소에서 자체 재생에너지와 ESS를 전력시장을 거치지 않고 충전에 사용할 수 있도록 제도가 개선되었는데, 이를 통해 고속충전 인프라가 야기하는 배전계통의 부담을 완화시키는 방안이 도출될 수 있을지 기대된다.)


운전자 별 충전 행태의 다양성 및 임의성

전기차 부하 예측에서 어려운 점은, 전기차 운전자들의 충전 행태가 운전자별로 굉장히 다양하며 (heterogeneous) 확률적이라는 (probabilistic) 것이다.

어떤 사람은 주로 집에서 야간 완속충전을 하는 반면, 어떤 사람은 주로 공용충전소에서 주간에 급속충전을 한다. 또 어떤 사람은 직장에 충전설비가 있어 직장에서 주간에 완속충전을 한다. 즉 충전 행태가 다양하다. 한편, 이는 행태가 비슷한 운전자들의 ‘grouping’의 필요성도 암시한다.

또한 같은 운전자라도 충전 행태가 매일 완벽히 똑같진 않을 것이다. 오늘의 정확한 충전 시간대가 어제와는 몇 분 이상 다를 수 있고, 오늘의 충전량 또한 어제의 충전량과 조금은 다를 수 있다. 심지어는 같은 운전자가 오늘 충전 시 어제와는 다른 장소에서 충전할 수도 있다. 즉 운전자가 ‘오늘 언제 어디서 얼마나 충전할지’는 고정된 상수가 아닌 확률변수로 보아야 한다.

위와 같이 다양하고 확률적인 운전자 별 충전 행태를 고려한 충전 부하 예측을 위해서는, 운전자들의 실제 충전 이력 데이터에 기반한 통계학습 모델을 구성하는 것이 좋다.


논문에서 제안하는 모델의 concept

이 포스팅에서는, 운전자들의 충전 이력 데이터셋을 이용해, 전기차가 많이 보급될 경우 특정 지역 내에서 하루 24시간 동안의 전기 부하가 어떻게 증가할지를 예측하는 모델을 제안한 논문을 소개한다. Applied Energy에서 출판된 ‘Scalable probabilistic estimates of electric vehicle charging given observed driver behavior’ 이다.

해당 논문에서 제시한 모델의 목적은, 각 전기차 운전자 별로 아래 요소들로 표현되는 충전 행태를 시뮬레이션하고, 그 결과를 합하여 ‘운전자들의 전기차 충전부하의 총 합’ 을 시간별로 예측하는 것이다.

1) 어디에서 어떤 인프라로 충전하는가?
2) 몇 시 몇 분에 충전을 시작하는가?
3) 충전 시간은 얼마나 걸리는가?
4) 충전 에너지의 양은 얼마나 되는가?

위 요소 중 1)에 해당하는 장소 및 인프라 종류는 segment라고도 하며, 이 연구에서는 아래 5가지를 고려하였다.

a) 단독주택에서의 저속 (6.6kW) 충전
b) 공동주택에서의 저속 충전
c) 직장에서의 저속 충전
d) 공용충전소에서의 저속 충전
e) 공용충전소에서의 고속 (50~150kW) 충전

제안된 모델은 앞서 언급한 이슈들인 다양성과 임의성을 고려하여 시뮬레이션이 가능하다는 장점이 있다. 아래 그림처럼 전기차 운전자들을 충전 행태의 유사도에 따라 grouping하여 충전 행태의 다양성을 반영할 수 있고, 특정 그룹에 속하는 운전자가 어떤 유형의 충전인프라를 언제 얼만큼 사용할지에 대한 확률분포를 모델링해 시뮬레이션한다.

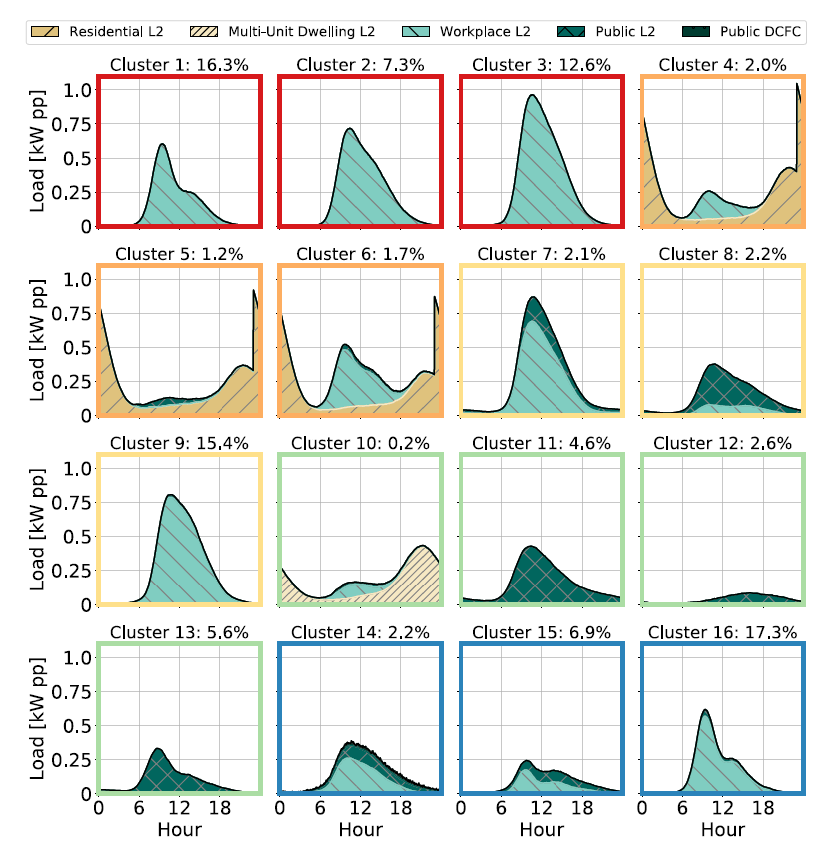clusters_ev 각 운전자 group 별 시간별 충전 부하 형태 (normalized profiles). 각 색깔은 각 segment를 의미함.

이를테면 위 그림에서 cluster 1~3 (붉은 테두리) 은 ‘충전의 대부분을 직장에서 주간에 하는 운전자들의 group을, cluster 4~6 (주황 테두리) 는 ‘충전의 대부분을 주택에서 야간에 하는 운전자들의 group’ 을 의미한다.

이 논문에서 제안된 모델을 통해, 일정 규모 이상의 발전/ 송전/ 배전 계획에서 전기차 확산의 영향을 보다 정확히 예측할 수 있을 것으로 기대된다.

실제로 해당 연구의 후속 연구 (Charging infrastructure access and operation to reduce the grid impacts of deep electric vehicle adoption) 는 Nature Energy에 게재되기도 했다.


비슷한 운전자들을 grouping (Clustering analysis 기반)

충전 행태가 ‘비슷한’ 운전자들 별 group들을 구성하기 위해 clustering analysis가 사용되었다. 운전자 별 유사도 판단에 사용할 운전자 별 정량적 속성 (quantitative feature) 들은 아래와 같다.

1) (일정 기간 내에) 각 segment에서 충전한 횟수
2) 각 segment에서의 평균적인 도착 시간
3) 각 segment에서의 평균적인 충전량
4) 각 segment에서의 평균적인 충전 시간
5) 각 segment에서 평일 대비 휴일 충전의 비율 (횟수 기준)
6) 전기차 배터리 용량
7) 충전하는 장소 수 (주소 기준)

(위 7개 feature들 중 1) ~ 5) 는 모든 segment 각각에 대해 별도로 계산됨에 주의.)

각 feature별로 단위 및 scale이 다르므로 normalization을 한 후, normalized feature vector space에서의 Euclidean distance에 기반해 clustering을 수행한다.

이 논문에서는 가장 흔히 사용되는 $k$-Means가 아닌, 계층적 (hierarchical) 구조를 고려하는 agglomerative clustering을 사용하였다. 이는 bottom-up 방식의 방법으로, 각 data point를 하나의 cluster로 두고 시작해 매 step마다 ‘가장 비슷한’ 두 cluster들을 하나의 cluster로 묶는 작업을 반복하는 알고리즘이다.

Agglomerative clustering을 하면 각 cluster의 의미를 파악하기 쉽다는 장점이 있다. 이 연구에서는 각 cluster의 의미가 중요하기 때문에 채택하였다.

이 연구에서는 cluster 갯수를 16개로 결정하였다 (elbow curve에 근거함). 16개 cluster들을 위에서 언급한 ‘의미’에 따라 보면, 각 운전자가 아래 5개의 ‘super’cluster들 중 하나에 속하는 것으로 해석할 수 있다.

1) 거의 대부분 직장에서 충전 (아래의 A-Red)
2) 거의 대부분 집에서 충전 (아래의 B-Orange)
3) 거의 대부분 공용충전소에서 충전 (아래의 C-Yellow)
4) 직장 및 공용충전소에서 충전, 배터리 크기 큼 (아래의 D-Green)
5) 직장 및 공용충전소에서 충전, 배터리 크기 작음 (아래의 E-Blue)

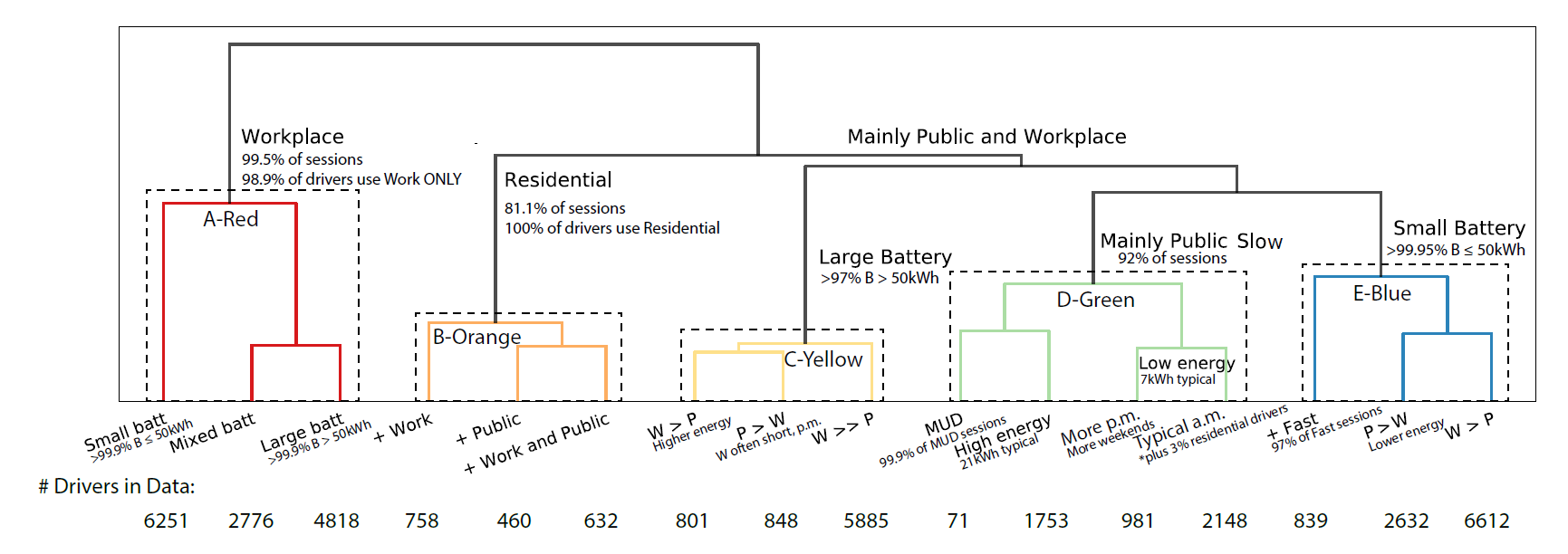dendrogram Clustering 결과의 의미를 해석하기 위한 dendrogram 및 5개의 supercluster들.

어떤 운전자가 16개의 cluster 중 특정 cluster $G$에 속할 확률을 $P(G)$라 표현한다. $P(G)$는 통상적으로 훈련 데이터에서의 각 cluster 별 크기에 기반해 결정하지만, 현실에 맞게 조정할 수 있다.

이를테면, 이 논문의 case study에서는 집에서의 야간 완속충전 비중이 증가하는 추세를 반영하여, 집에서의 야간 완속충전을 위주로 하는 운전자들에 대응하는 supercluster (위에서의 B-Orange) 의 $P(G)$를 증가시켰다.


각 운전자의 충전 장소/ 인프라 확률 모델링

서두에서 언급했듯, 전기차 충전 장소와 인프라 유형 (segment라 칭함) 으로 아래 5가지를 고려하였다.

a) 단독주택에서의 저속 (6.6kW) 충전
b) 공동주택에서의 저속 충전
c) 직장에서의 저속 충전
d) 공용충전소에서의 저속 충전
e) 공용충전소에서의 고속 (50~150kW) 충전

각 cluster 별 운전자는 꼭 하나의 segment에서만 충전하는 것은 아니다. 빈도의 차이는 있지만, 그때그때 다른 segment에서 충전할 수 있다. 이를테면 대부분의 충전을 주택에서 하는 운전자도, 불가피하게 장거리 운전을 하다 도중에 공용충전소에서 충전할 일도 있을 것이다.

그러므로 각 cluster 별로, cluster $G$에 속하는 운전자가 하루 동안 segment $z$에서 충전할 확률 $P(z \vert G)$를 추정한다.

평일에 대해서는, 그 group 내 모든 운전자들이 데이터 수집 기간 동안의 총 평일 수 대비 해당 segment $z$에서 충전한 평균횟수의 비율로 추정하였다. 휴일에 대해서는 같은 논리로 별도의 확률을 추정한다.


각 운전자의 충전 시작시간/ 에너지량/ 소요시간 확률 모델링

Cluster $G$에 속하는 운전자가 segment $z$에서 충전할 때, 충전소에서 충전을 시작하는 시간/ 충전 에너지량/ 충전에 걸리는 시간 총 세 가지 변수의 묶음을 3변량 확률변수 벡터 $s$로 보고, 해당 벡터의 다변량확률분포 $P(s \vert z,G)$를 모델링한다.

이 연구에서는 Gaussian Mixture Model (GMM) 을 사용하였다. 즉 확률분포를 단일한 정규분포가 아니라 여러 개의 정규분포들의 합 (즉 multimodal distribution) 으로 가정하였다.

이는 같은 group과 같은 segment라 하더라도 사람들에 따라 디테일한 충전 행태가 다를 것이고 (누구는 이른 시간에 와서 조금만 충전하고, 누구는 늦은 시간에 와서 많이 충전하고 등), 특별히 빈도가 높은 행태가 한 가지가 아니라 두 가지 이상일 수 있기 때문이다.

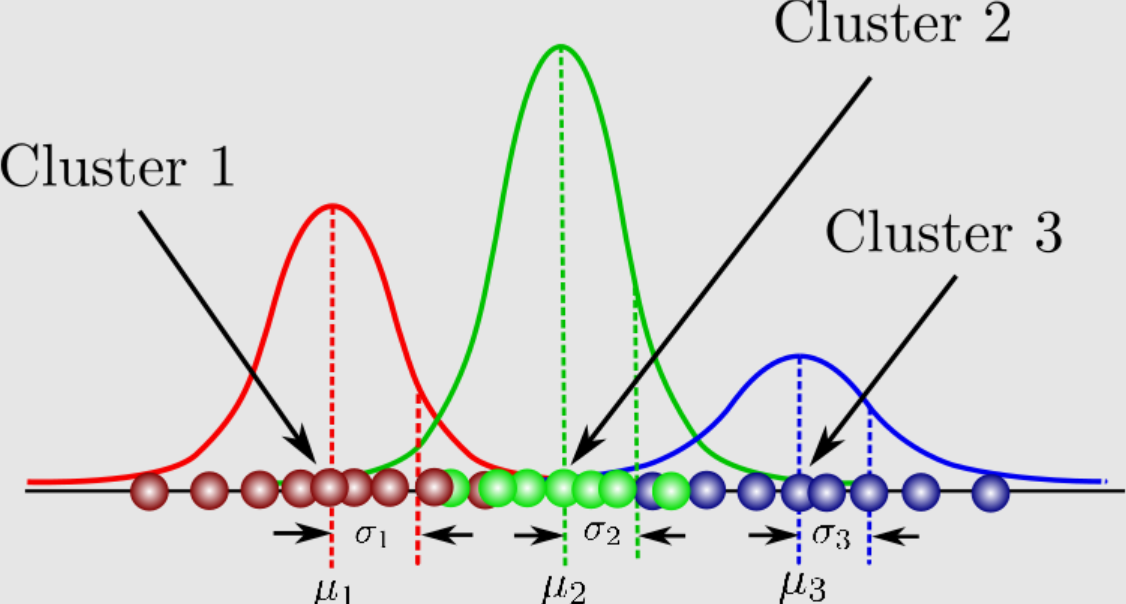gmm_concept Gaussian Mixture Model의 concept. 빈도가 높은 값이 여러 개 있음.

GMM에서는 component (각각의 단일한 3변량 정규분포) 의 갯수를 사전에 정해 주면, 각 component 별 평균 벡터와 공분산 행렬 및 각 component의 가중치를 (데이터에 가장 잘 적합되게) 계산한다.

각 $(z,G)$ 별 GMM 모델의 component 갯수를 정하려면 지표가 필요한데, 이 논문에서는 Akaike Information Criterion (AIC) 를 지표로 두어 데이터에 잘 적합되면서도 복잡하지 않은 모델을 도출하도록 하였다.

이를테면, 아래 그림에서 상단의 큰 subplot은 특정 cluster에 속하며 직장에서 주간 완속충전을 하는 사람 1만명을 가정하고 시뮬레이션해 얻은 시간별 총 충전 부하이고, 하단의 4개 subplot들은 해당 $(z,G)$에 대한 GMM 모델의 component들 중 가중치가 높은 순으로 4개 component들 각각에 의해 도출된 시간별 충전 부하다.

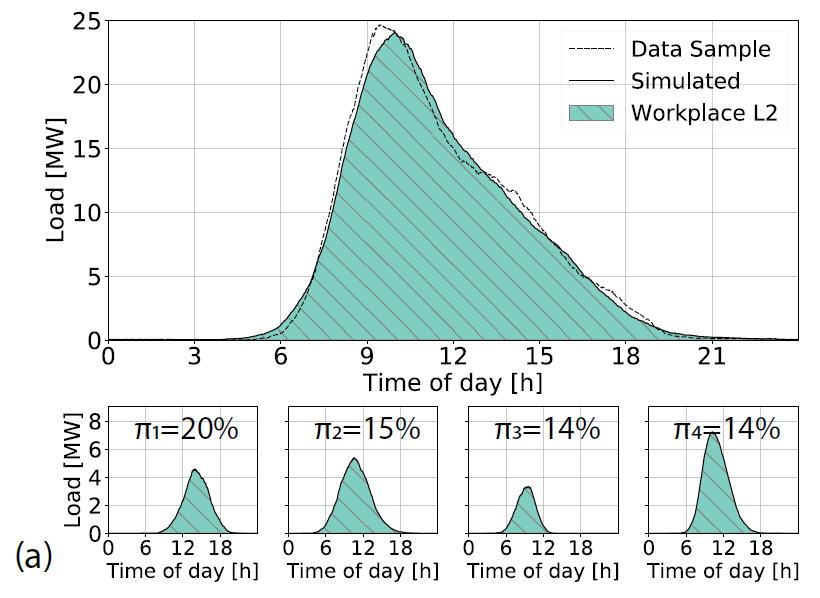Gaussian_mixture 특정 cluster - segment 조합에 대한 운전자 1만명을 시뮬레이션했을 때의 충전 패턴 (상단) 및 GMM의 major component들에 의해 계산된 패턴들 (하단).

여기까지 계산하면, 각 운전자의 cluster/ segment/ 디테일한 충전행태 (충전 시작시간/ 에너지량/ 소요시간) 의 ‘결합’ 확률분포 $P(s,z,G)$ 를, 앞에서 구한 확률분포들의 곱인 $P(s \vert z,G) P(z \vert G) P(G)$ 로 계산할 수 있다.

위 확률분포 곱을 얻으면, $G$를 생성하고, 주어진 $G$를 조건부로 하는 $z$를 생성하고, 주어진 $(z,G)$를 조건부로 하는 $s$를 생성하여, 각 운전자의 충전 부하를 시뮬레이션으로 생성할 수 있다.


논문의 case study: 시나리오 소개

논문에 사용된 데이터셋은 California의 특정 충전소 사업체로부터 받은, 약 38,000명의 운전자가 약 399만 회 충전한 이력 데이터이다.

논문에서는 2030년에 전기차 수가 8백만대로 증가한다고 가정하고, 하기의 4개 시나리오 각각에 대해 총 전기차 충전 부하를 시뮬레이션하였다.


시나리오 1: 주택에서의 충전이 계시별 요금제 및 타이머 기반으로 이루어질 경우

모델링에 사용된 충전 이력 데이터에 따르면 대부분의 충전이 직장에서 이루어졌다. 그러나 이는 해당 충전소 사업체의 특성에 영향받은 결과이다. 실제로 California에서는 주택에서의 충전이 증가하는 추세이며, 2030년에는 운전자의 3분의 2가 주택에서 충전할 것으로 예상된다.

그러므로 16개 cluster들 중 거의 대부분 주택에서 충전하는 운전자들에 대응하는 3개 cluster (위 dendogram에서의 B-Orange) 에 대한 $P(G)$의 합이 67%가 되게 확률을 조정하였다.

또한 주택 충전의 3분의 2가 타이머 기반 자동 충전 (오후 11시 또는 자정에 시작) 을 할 것으로 예상된다. 그러므로 시나리오 1에서는, 각 cluster의 운전자가 segment들 중 주택에서 충전할 경우의 GMM 모델에 대해 타이머 기반 자동 충전에 대응되는 component들의 weight를 증가시켰다.


시나리오 2: 주택에서의 충전이 임의적으로 이루어지는 경우

시나리오 1에서는 주택의 계시별 요금제 및 타이머 기반 자동 충전을 가정했다. 그러나 실제로는 주택 사용자들이 계시별 요금제를 채택하지도 않고 그 결과 타이머 기반 충전을 하지 않을 수도 있다. 일종의 ‘uncontrolled charging’ (임의적 충전) 으로 볼 수 있다.

시나리오 2에서는 uncontrolled charging을 시뮬레이션한다. 이를 위해 시나리오 1과는 반대로, 타이머 기반 자동 충전에 대응되는 component들의 weight를 감소시켰다.


시나리오 3: 직장에서의 충전 시간대를 분산시키는 경우

거의 대부분을 직장에서 충전하는 운전자들에 대응하는 cluster들에 대한 시간별 충전 profile을 보면 (위 16개 cluster 각각의 충전 profile 그림의 1~3번째), 대략 10시 경에 뾰족한 피크부하가 형성된다. 이는 직장에서 충전하는 운전자들 대다수가 직장에 도착하자마자 (즉 비슷한 시간에) 충전을 시작하기 때문으로 추정된다.

이러한 피크부하는 계통에 부담을 주므로, 부하 평준화가 필요하다. 시나리오 3에서는, 어떤 인센티브 정책에 의해 직장에서 충전하는 운전자들의 상당수가 정오 이후에 충전을 시작하는 경우를 시뮬레이션한다.

이를 위해, 직장에서도 충전하는 운전자들이 직장에서 충전할 경우의 GMM 모델에 대해 정오 이후의 충전에 대응되는 component들의 weight를 증가시켰다.


시나리오 4: 재택근무자 증가로 주택에서의 아침~오후 충전 비중이 증가할 경우

시나리오 1과 2에서는 주택에서의 충전이 거의 대부분 야간에 이루어진다고 가정했다. 그러나 최근 재택근무 (working from home) 이 증가하고 있다. 이 경우, 주택에서의 충전 중 아침~오후 시간대에 이루어지는 충전의 비중이 증가할 수 있다.

시나리오 4에서는, 주택에서 충전하는 운전자들의 cluster (dendogram에서의 B-Orange) 및 주택 segment 내 충전에 대한 GMM 모델에서 아침~오후 시간대 충전에 대응되는 component들의 weight를 증가시켰다.


논문의 case study: 결과 (주택 내 충전에 의한 야간 피크부하 발생)

4개의 시나리오 각각에 대해, 전기차 8백만대가 하루 동안 발생시킬 것으로 예측되는 총 충전 부하를 시뮬레이션한 결과는 아래 그림과 같다.

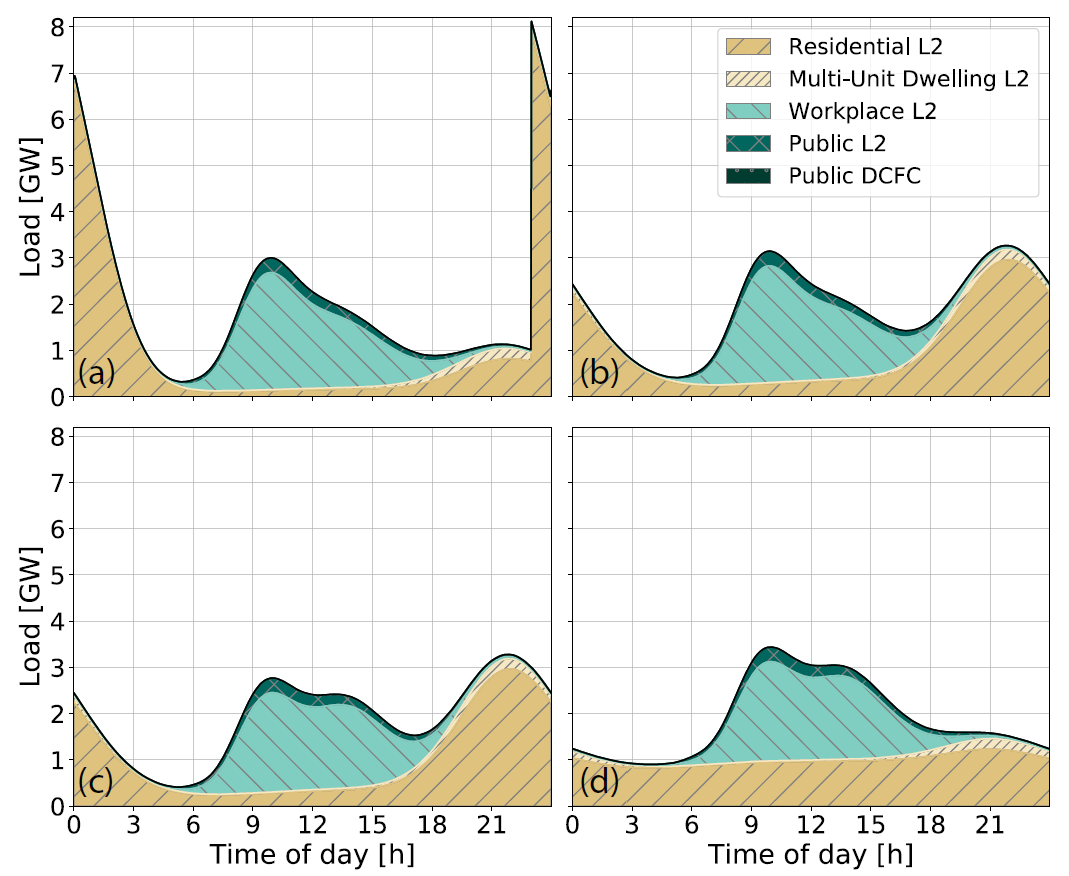scenarios 4개 시나리오에 대해 전기차 8백만대의 총 충전 부하를 시뮬레이션한 결과.

주목할 부분은 시나리오 1 (위 그림의 (a)) 에서 야간에 발생하는 피크부하 (약 7GW) 및 오후 11시를 기점으로 하는 부하 급증이다. 이는 대부분의 운전자가 계시별 요금제에 대응하여 특정 시간에 충전을 시작하도록 타이머를 쓰고, 그 결과 대부분의 주택 운전자들의 충전 시작 시간대가 거의 같아지기 때문이다.

현재 California 전력계통의 주간 피크가 약 25GW임을 감안하면, 계시별 요금제 적용 시 주택 내에서 타이머에 기반해 이루어지는 전기차 자동 충전에 의해 매우 큰 야간 피크부하가 발생하고, 심지어 해당 피크부하 발생 직전의 ramp rate 또한 매우 커서, 계통 안정성이 위협받을 것으로 추정된다.

따라서 향후 주택 내 전기차 충전 요금제는, 운전자들의 충전 시작 시간을 분산시킬 수 있도록 설계할 필요가 있다는 결론을 얻는다.


저자의 data-driven modeling 강의

해당 연구를 주도한 연구자이자 논문 교신저자인 Ram Rajagopal (Stanford Univ.) 가, 해당 연구 내용을 포함하는 세미나 ‘Data-Driven Modeling of Distributed Energy Resources and Applications’ 를 DTU Summer School 2023에서 진행하였다 (아래 영상 참고).