에너지시스템 최적화/게임이론 강의: 1) Market clearing as an optimization problem
이 포스팅은, Technical University of Denmark의 박사과정 과목 “Advanced Optimization and Game Theory for Energy Systems” (Prof. Jalal Kazempour) 의 1강을 필자가 요약한 내용이다.
Market clearing price 결정
Market clearing이란, ‘수요와 공급을 일치시킬 때의 (단일)가격을 결정하는 과정’이다.
이를테면 아래 슬라이드처럼, 두 개의 발전기와 두 개의 수요처가 전력시장에서 offering 및 bidding을 할 경우를 보자.

위 예시에서 두 수요처의 최대 부하의 합이 각 발전기의 개별 용량보다 크므로, 두 발전기 모두 가동되어야 한다.
한편 위 예시에서는 전기 가격이 MWh당 20달러에서 35달러 사이의 어떤 숫자가 되어도 거래가 성립할 것이다. 수요처 입장에서 bidding price보다 낮은 가격이기 때문이다. 그렇다면, market clearing price는 왜 20달러로 결정되었을까?
이는 market clearing price가 social welfare (또는 market surplus) 를 최대화하게끔 결정되기 때문이다.
전력시장에서 social welfare는, ‘수요처가 bid price보다 저렴하게 전기를 구입해서 얻는 utility’ 에서 ‘발전기가 전기를 생산하는데 드는 비용 (offer price와 같다고 가정)’ 을 뺀 값으로 정의된다. (이 때, 발전기가 offer price를 발전단가 즉 production cost로 ‘정직하게’ 설정했다고 가정한다.)
Social welfare를 최대화 대상 목적함수로 하는 ‘최적화 문제’는 아래 슬라이드와 같다.

그런데 위 문제에서 변수는 각 발전기의 발전량 및 각 수요처의 전력부하이다. Market clearing price는 위 수식에서 보이지 않는다. 어디 있는 것일까?
Market clearing price는 수요-공급 일치 (balance) 조건의 dual variable이다.
특정 제약조건에 대한 dual variable은 ‘optimal point에서 목적함수가 해당 제약조건의 perturbation에 따라 변하는 정도, 즉 sensitivity’ 이다. Balance의 perturbation은 전기 수요 또는 공급량의 변화이므로, 단위 변화량 당 비용으로 생각하면 가격을 의미함은 자명하다.

Network 제약 하의 nodal price
실제로는 아래와 같이 여러 개의 bus가 존재하고 bus 간에 송전망에 의한 송전량 제약이 있으며, 각 bus별로 가격이 다를 수도 있다.
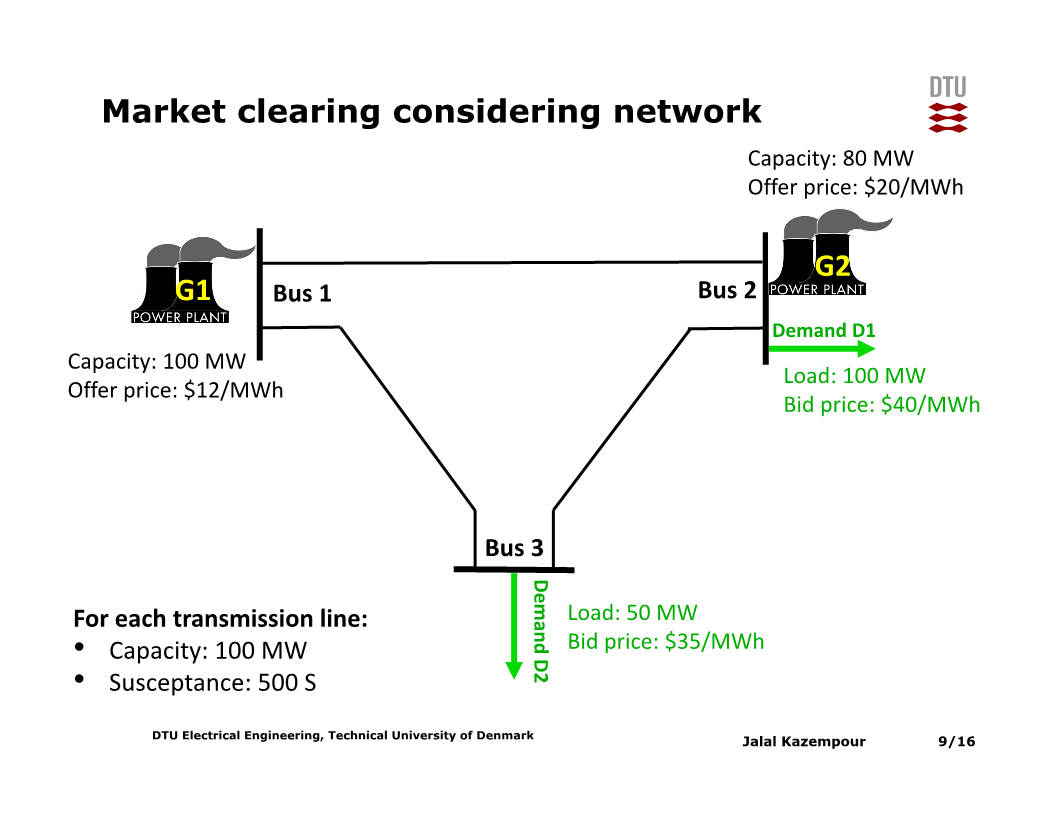
DC power flow 근사 하에서, bus $n$에서 bus $m$으로 흐르는 전력은 $f_{n,m} = B_{n,m} (\theta_n - \theta_m)$ 으로 계산된다. (B는 susceptance, $\theta$는 voltage angle). 그러므로 voltage angle 기반 송전 제약을 추가한 최적화 문제를 아래와 같이 구성한다.
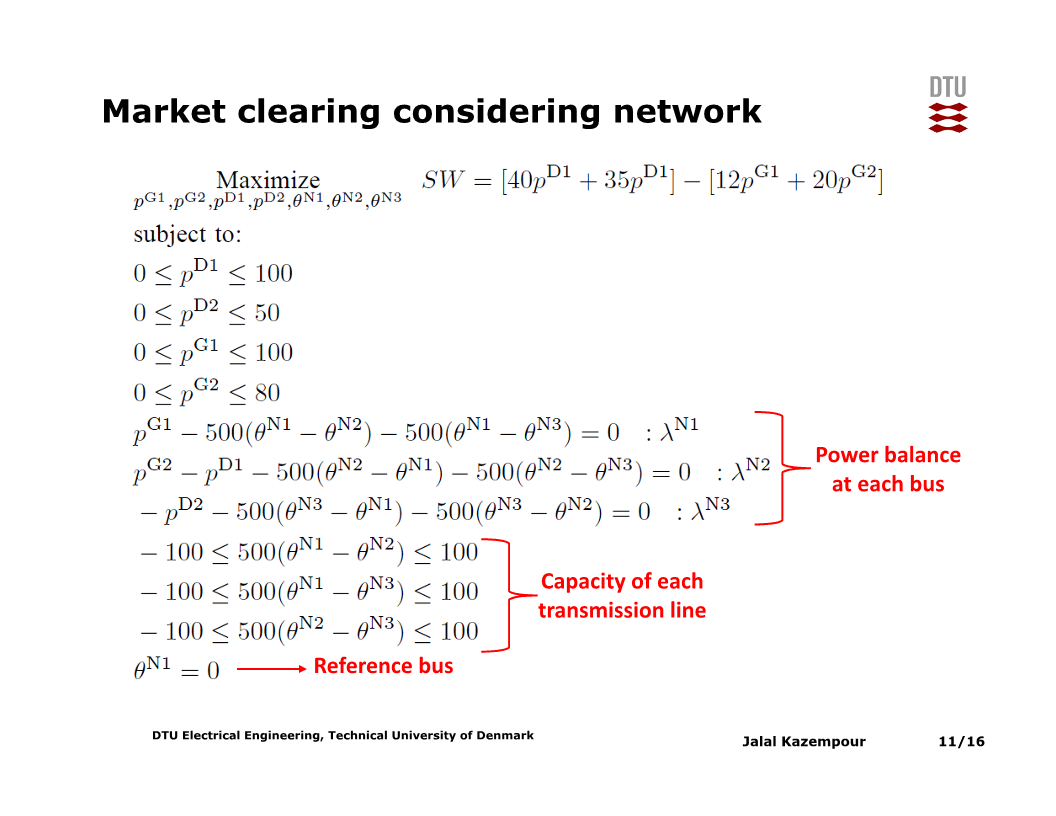
위 문제에서 capacity of each transmission line 제약의 하한이 0이 아니라 -100 임에 주의한다 (마이너스는 반대 방향으로의 흐름을 의미한다).
‘각 bus에서의’ power balance 제약 각각에 대한 dual variable이 각 bus 별 ‘nodal’ price이다. 이러한 node 별 단일가격 기반 시장을 LMP (Local Marginal Price) based market이라 한다.
Node 별 price는 congestion이 없을 경우 (즉 어떤 송전선에서도 송전량이 송전 상한에 도달하지 않은 경우, 수학적으로 말하면 송전량 제약들이 전부 inactive한 경우) 에는 전부 같다. 그러나 congestion이 있을 경우 node별로 가격이 달라질 수 있다.
01) Market clearing as an optimization problem
02) Market clearing as an equilibrium problem
03) Desirable properties of market-clearing mechanisms
04) Market clearing using a cooperative game approach
05) Stochastic market clearing
06) Robust approaches for market clearing
07) Bilevel programming in energy systems
08) Optimization problems with decomposable structure
09) Benders’ decomposition: Theory
10) Benders’ decomposition: Applications
11) Augmented Lagrangian relaxation
12) Variants of ADMM and applications