에너지시스템 최적화/게임이론 강의: 9) Bender’s decomposition
이 포스팅은, Technical University of Denmark의 박사과정 과목 “Advanced Optimization and Game Theory for Energy Systems” (Prof. Jalal Kazempour) 의 9강을 필자가 요약한 내용이다.
Complicating variable의 값을 찾는 원리
Bender’s decomposition은, 모든 소문제에 공통적으로 포함되는 ‘변수’인 complicating ‘variable’이 있을 때 사용하는 decomposition method이다.
Complicating variable이 포함된 큰 문제를 여러 subproblem들로 쪼개기 위해서는, complicating variable의 값을 고정해야 한다. 그러면 그 고정값을 얼마로 해야 될까?
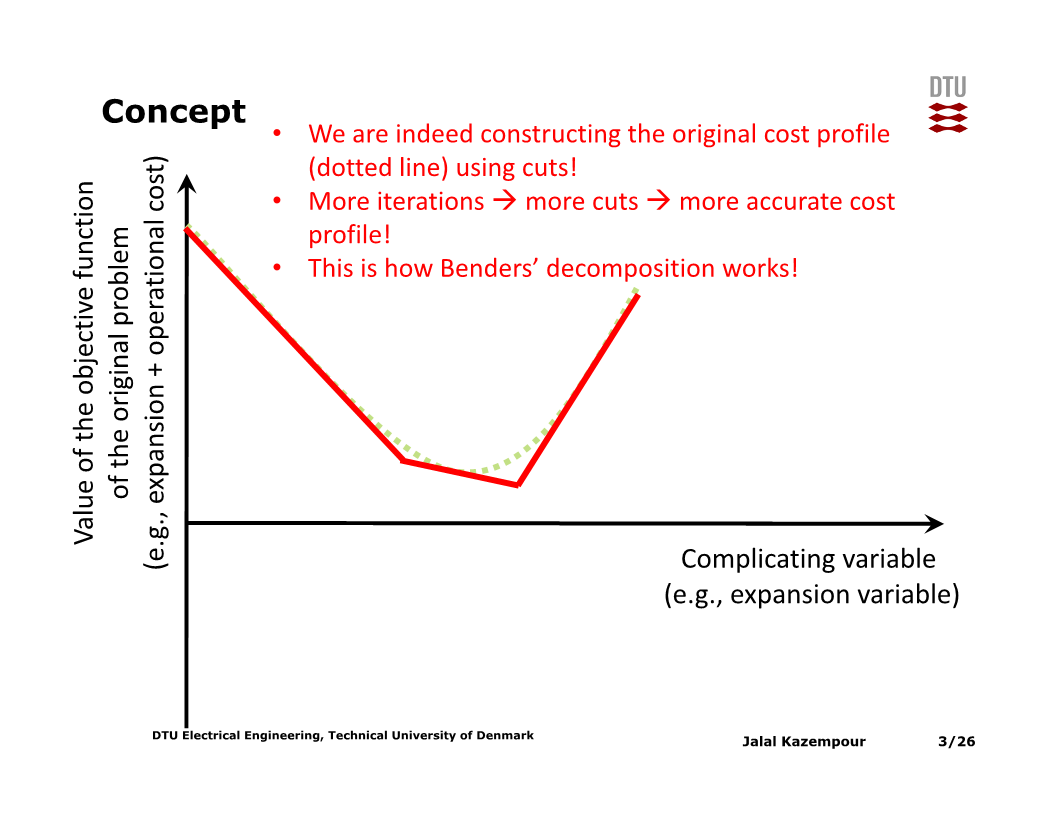
Complicating variable을 $x$라 할 때, $x$가 가질 수 있는 각 값들 별로 나머지 변수들에 대해 문제를 풀어 얻은 목적함수 값들을 아래 슬라이드와 같이 plot할 수 있다고 하면, 목적함수가 최소가 되는 $x$값을 선택하면 된다.
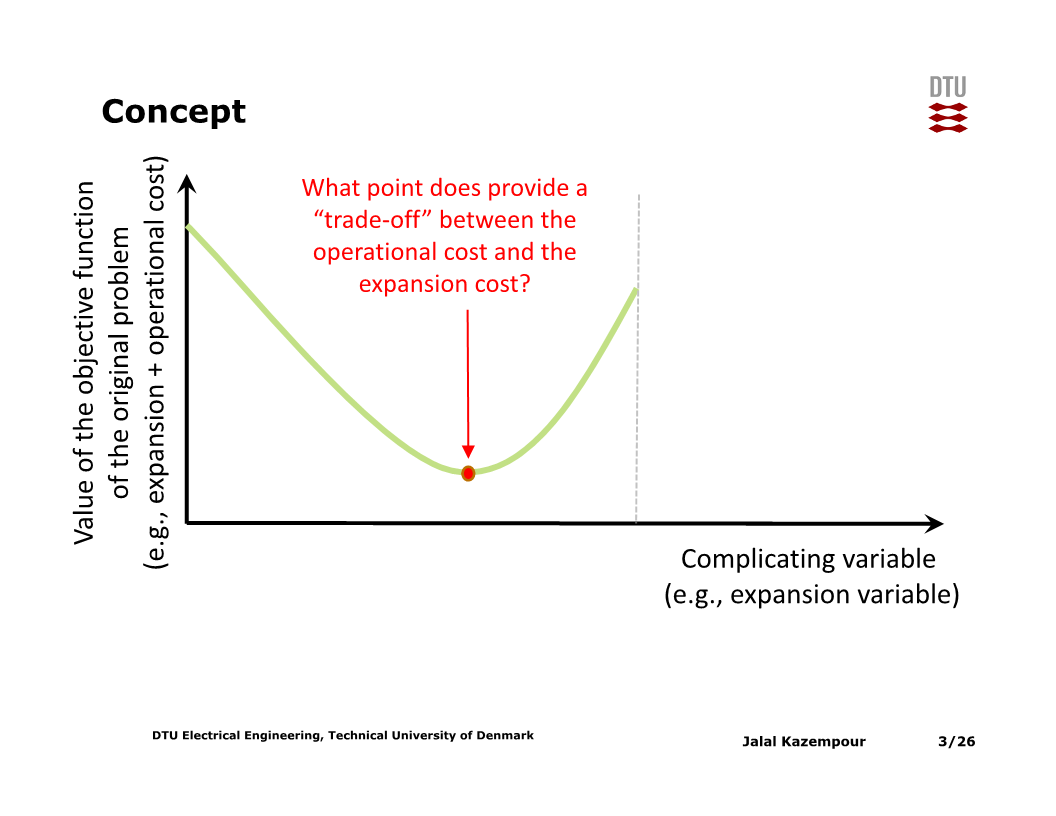
$x$가 ‘신규’ 발전설비의 용량이고 위 plot에서의 목적함수가 총 비용 (건설비용과 운영비용의 합) 이라 하면, $x$가 작아서 목적함수의 값이 큰 상황은 ‘발전설비 부족으로 전력 공급에 어려움을 겪을 경우의 운영비용 증가’, $x$가 커서 목적함수의 값이 큰 상황은 ‘발전설비를 필요 이상으로 과하게 건설할 경우의 고정비용 증가’ 로 볼 수 있다.
실제로는 위와 같은 plot을 미리 알 수 없다. 그러나 다행히도, 위 plot을 piecewise-linear function으로 근사하는 방법이 있다.
먼저 $x$의 initial point를 정하고, 해당 $x$값으로 고정 후 목적함수를 계산한다.
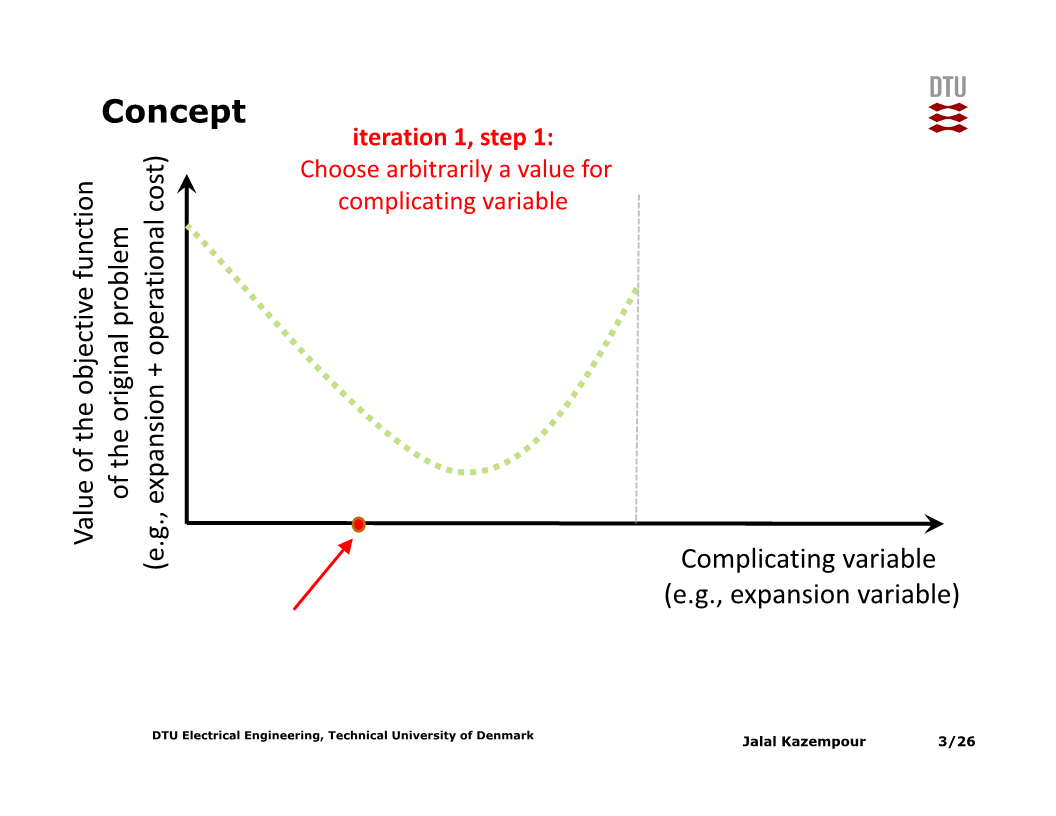
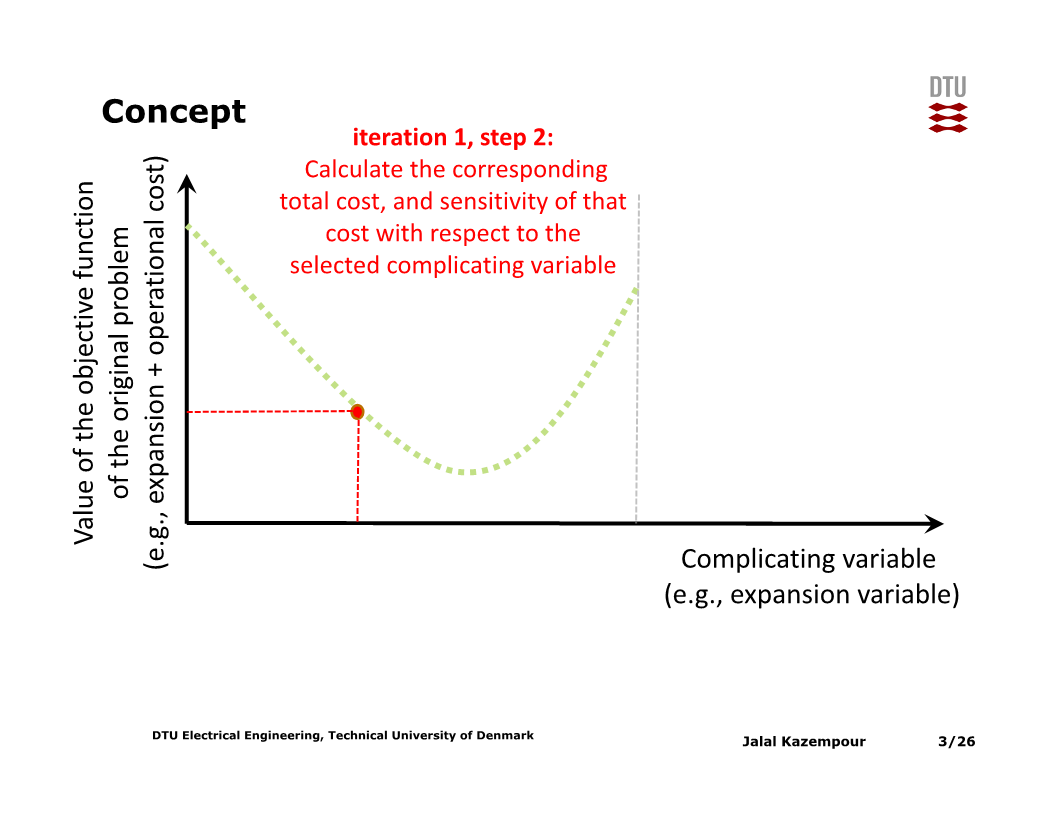
다음으로 해당 $x$값에서 목적함수의 sensitivity 값 기반으로 접선을 계산한다 (subproblem의 dual variable을 계산해 얻으며, 자세한 내용은 뒤에서 설명한다).
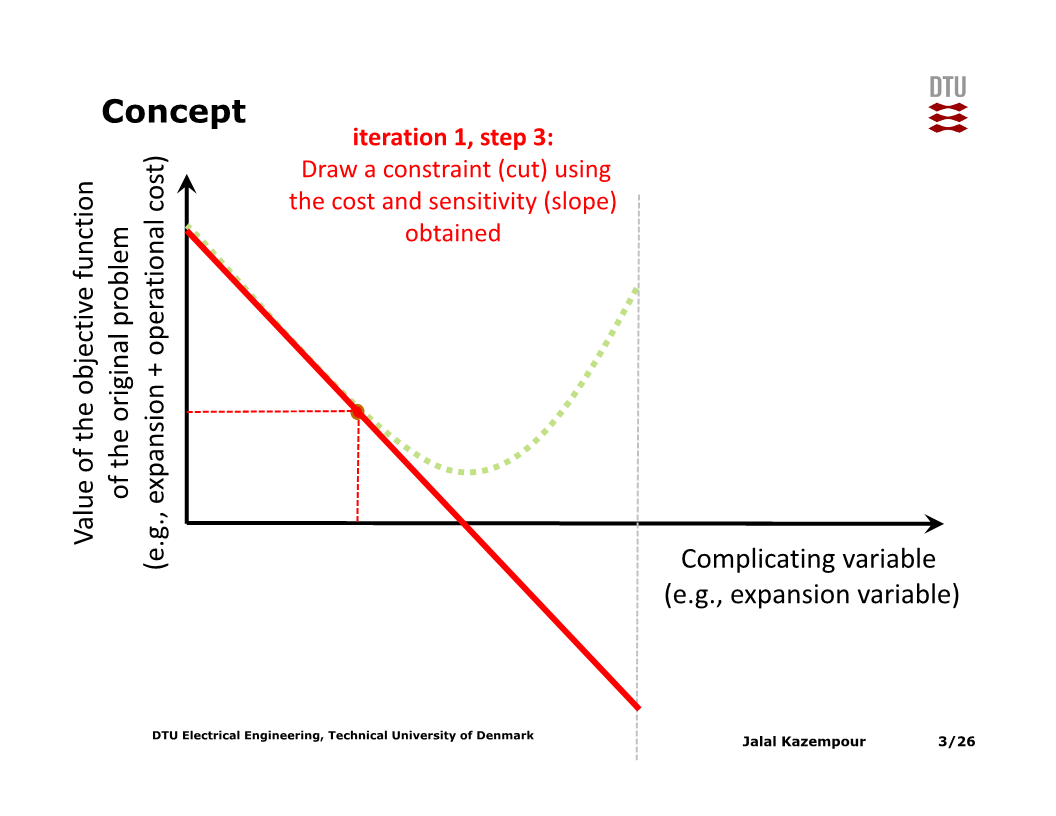
이 접선을 기준으로 목적함수를 최소화하는 $x$값을 구하고, 해당 $x$에 대해 위 과정을 다시 수행한다.
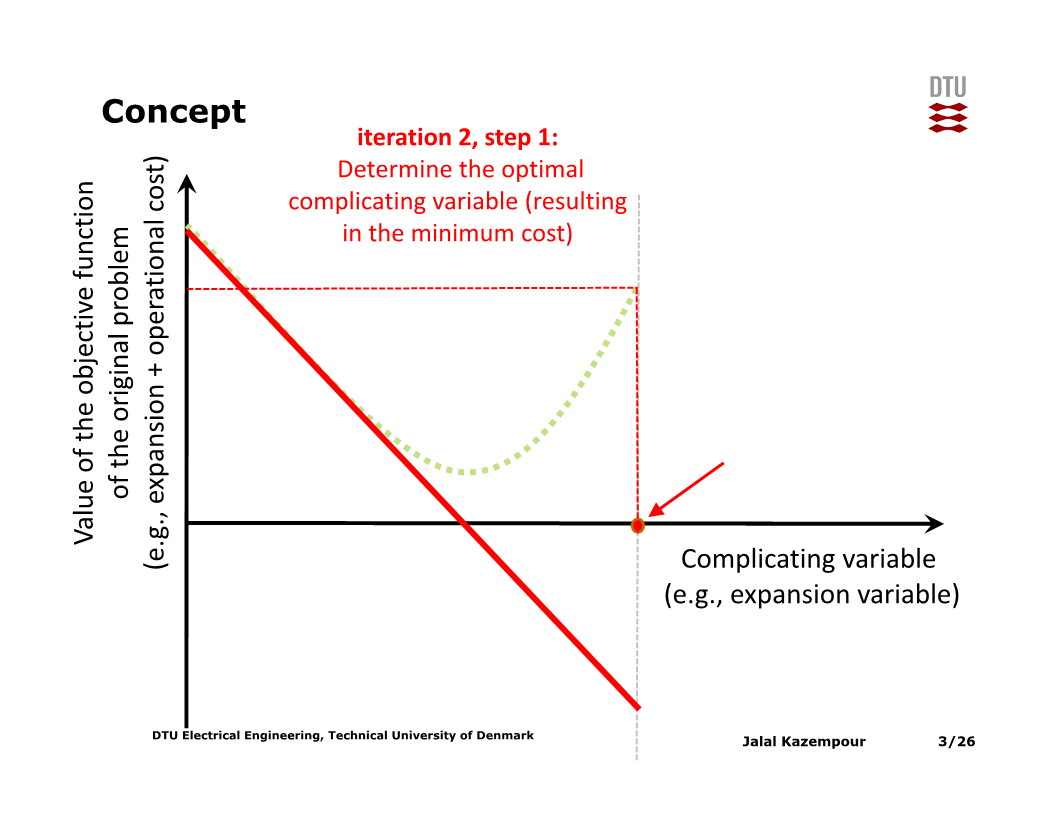
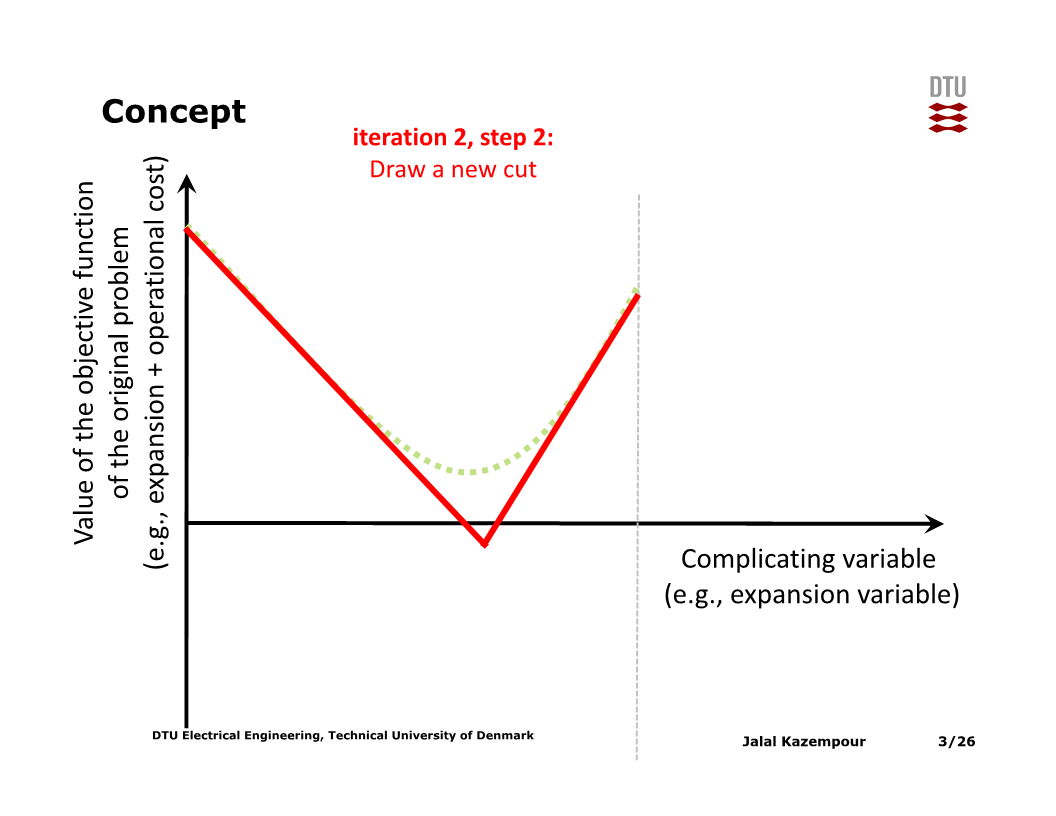
그러면 접선 두 개가 이루는 piecewise-linear function이 생기는데, 해당 function을 기준으로 목적함수를 최소화하는 $x$값을 구하고, 해당 $x$에 대해 위 과정을 다시 수행한다.
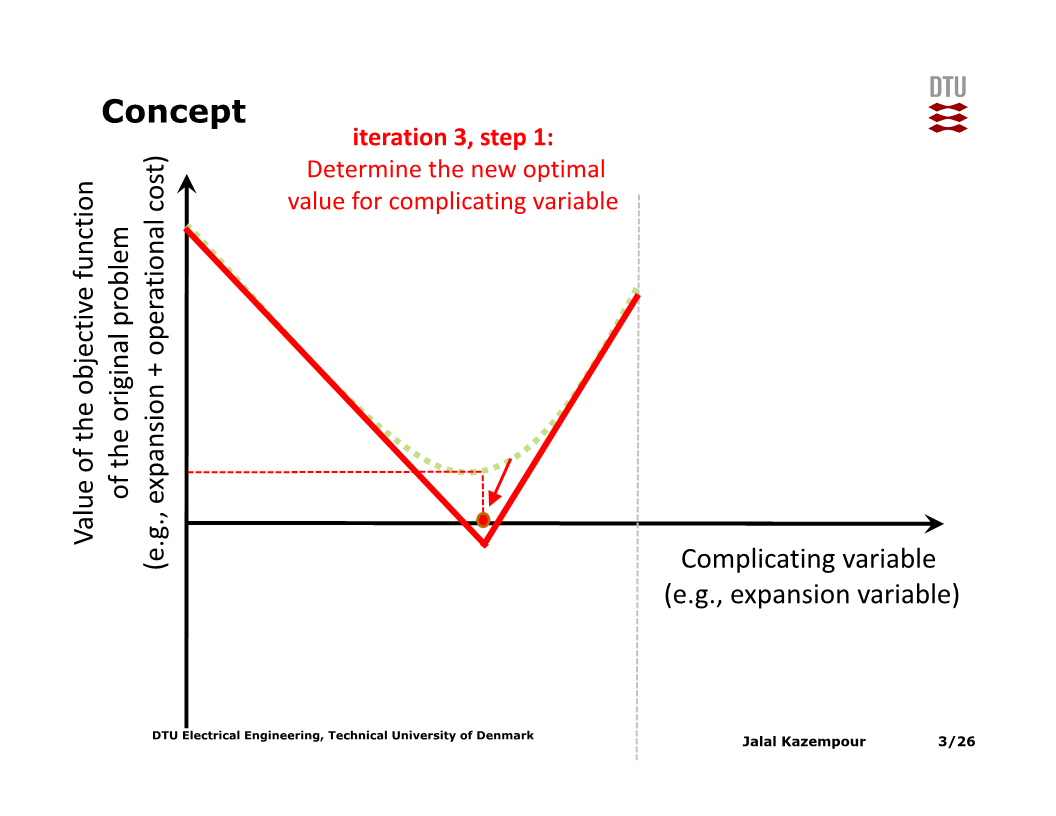
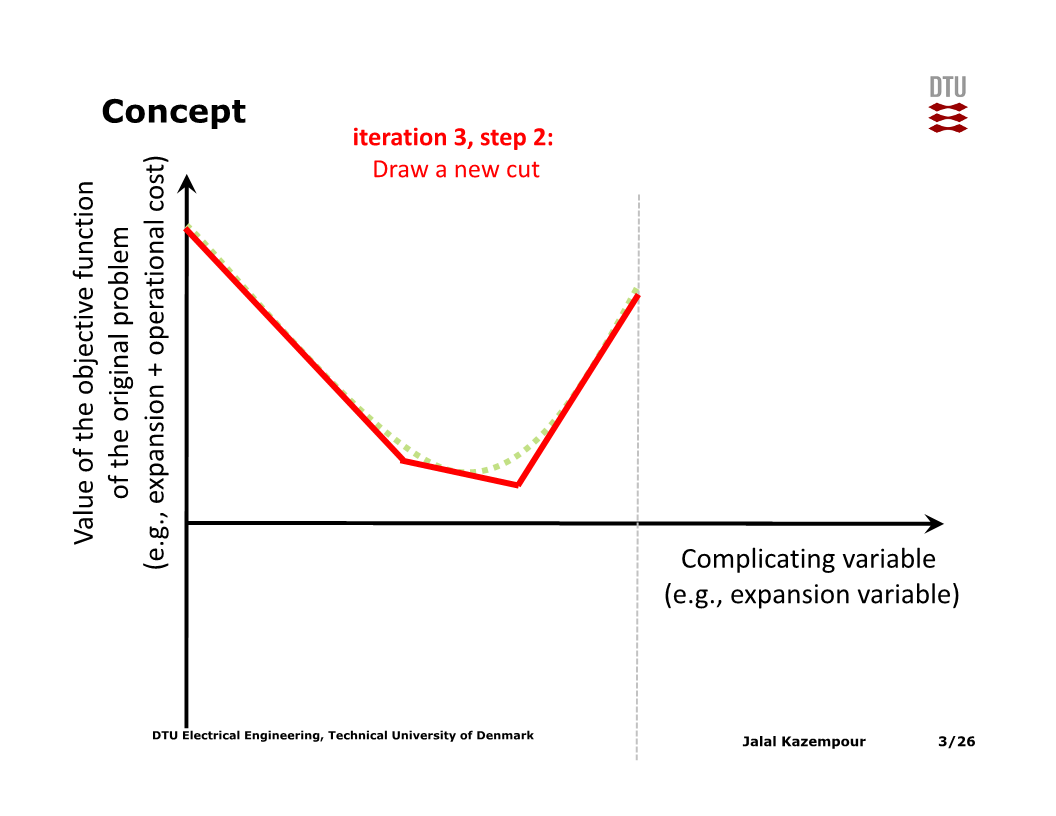
이 과정을 반복할수록, piecewise-linear function이 $x$값과 목적함수 간의 실제 관계와 유사해진다. 그러므로 이 과정을 수렴 조건이 만족될 때까지 반복한다.
(단, $x$값과 목적함수 간의 관계가 convex임을 전제로 한다. non-convex인 경우 local optimum에 도달할 수 있다. $x$가 벡터인 경우에도 $x$의 원소 각각에 대해 convex여야 한다.)
Bender’s decomposition 알고리즘
아래 슬라이드의 예제를 Bender’s decomposition으로 푼다고 하자. 여기서 $x$를 complicating variable로 본다.

그러면 $x$를 고정했을 때의 $y$에 대한 subproblem과, subproblem의 dual variable들 기반으로 구성할 수 있는 $x$에 대한 master problem은 아래 슬라이드와 같다.

Master problem에서 $\alpha^{(i)}$는 원래 문제의 목적함수에서의 $y$에 대한 term ($-y$) 을 대체하는 auxiliary variable이고, $i$는 iteration index이다 (여기서는 $i$가 1부터 시작한다고 둠). $\alpha^{down}$은 첫 번째 iteration에서 master problem을 bounded problem으로 만들기 위한 상수로, 크기가 매우 큰 음수이다.
$\pi^{(k)}$, $\mu^{(k)}$, $\sigma^{(k)}$, $\gamma^{(k)}$ 는 $k$번째 iteration에서의 subproblem의 dual variable의 값들이다. 이 때 $k=1,2,\cdots,i-1$, 즉 직전 iteration까지의 ‘모든 iteration 각각에 대한’ 값들을 전부 모은 것임에 주의한다. 즉 $\alpha^{(i)}$에 대한 부등호 제약조건이 $i-1$개가 있는 것이다. 그리고 첨자 $(i)$만이 변수이고 첨자 $(k)$는 전부 parameter들임에 주의한다.
$\alpha^{(i)}$에 대한 부등호 제약의 우변은 subproblem의 dual objective function이다. 실제로 $y$에 대한 subproblem의 Lagrangian을 쓰고 $y$ term들을 제거하면 ($y$ term들을 제거하지 않으면 unbounded problem이 됨), dual objective를 우변과 같이 얻는다. 그리고 $\alpha^{(i)}$는 최소화 대상이므로, $\alpha^{(i)}$는 $i-1$개의 dual objective 중 적어도 하나와 같은 값이 된다.
Duality theorem에 의해 primal problem의 목적함수 (여기서는 $-y$)는 dual problem의 목적함수 ($\alpha^{(i)}$에 대한 부등호 제약의 우변) 보다 크거나 같다. 그러므로 subproblem을 풀어 얻은 subproblem의 목적함수의 값은 $\alpha^{(i)}$보다 크거나 같다.
또한 subproblem이 linear programming problem이므로, optimal point에서는 primal problem의 목적함수와 $\alpha^{(i)}$가 서로 같을 것이다.
그러므로 primal problem의 목적함수를 UB (upper bound) 로, $\alpha^{(i)}$를 LB (lower bound) 로 두고, $\vert UB - LB \vert \leq \epsilon$ 이 될 때까지 반복한다. 알고리즘은 아래와 같다.

제약조건을 보다 간단히 쓰는 Compact form
위 설명대로라면, master problem의 $\alpha^{(i)}$에 대한 부등호 제약의 우변은 subproblem의 제약조건이 많을수록 매우 복잡해질 것이다 (dual variable 수가 늘어나므로). 게다가, 서두에 언급했던 $x$의 sensitivity를 기반으로 계산하는 방법도 아니다.
$\alpha^{(i)}$에 대한 부등호 제약의 우변을 보다 간단하게 쓰는 compact form은 아래와 같다.

Subproblem에서 $x^{(i)}$를 형식적으로는 변수로 두되 맨 마지막 제약조건을 통해 그 값을 master problem에서 얻은 값으로 고정한다. 이 경우 어쨌든 제약조건은 맞으므로 $x^{(i)}$에 대한 sensitivity $\rho^{(i)}$를 구할 수 있다.
Master problem에서는 subproblem의 목적함수 (여기서는 $-y^{(k)}$) 및 $x^{(k)}$에 대한 sensitivity $\rho^{(k)}$를 이용해서 $\alpha^{(i)}$에 대한 부등호 제약의 우변을 구성한다. 이는 훨씬 간단해진 compact form이자, 서두에 언급했듯 $x$의 sensitivity를 기울기로 하는 접선 계산이기도 하다.
Compact form의 $\alpha^{(i)}$에 대한 부등호 제약의 우변이 original subproblem의 dual objective와 동치 (equivalent) 임은 KKT condition 비교를 통해 확인할 수 있다.
01) Market clearing as an optimization problem
02) Market clearing as an equilibrium problem
03) Desirable properties of market-clearing mechanisms
04) Market clearing using a cooperative game approach
05) Stochastic market clearing
06) Robust approaches for market clearing
07) Bilevel programming in energy systems
08) Optimization problems with decomposable structure
09) Benders’ decomposition: Theory
10) Benders’ decomposition: Applications
11) Augmented Lagrangian relaxation
12) Variants of ADMM and applications