에너지시스템 최적화/게임이론 강의: 6) Robust approaches for market clearing
이 포스팅은, Technical University of Denmark의 박사과정 과목 “Advanced Optimization and Game Theory for Energy Systems” (Prof. Jalal Kazempour) 의 6강을 필자가 요약한 내용이다.
Worst-case scenario
이전 강의에서의 시나리오 기반 stochastic market clearing에서는, 하루전 시장 비용과 각 시나리오 별 실시간 시장 비용의 ‘기대값’의 합을 최소화하는 급전계획을 수립하였다.
여기서 더 보수적으로 접근한다면, ‘총 비용이 가장 많이 발생하는 시나리오’의 총 비용을 최소화하고자 할 수 있다. 즉 ‘worst-case’ 의 비용을 최소화하는 것이다.
이러한 접근을 ‘robust’ market clearing이라 하며, 시나리오 기반 robust market clearing 문제는 아래 슬라이드와 같다.

변수 $\beta$가 각 시나리오 별 실시간 시장 비용 중 최대값, 즉 worst-case에서의 실시간 시장 비용이다.
비용은 worst-case 시나리오만을 기준으로 계산되지만, 다른 시나리오들에 대해서도 위 최적화 문제가 풀 수 있는 (feasible) 문제이어야 함에 주의한다.
만약 풍력 발전량의 시나리오 4개가 각각 30MW, 60MW, 70MW, 40MW 일 경우 (네 번째 시나리오가 이전 강의에서의 10MW가 아님에 주의), robust market clearing 문제를 풀면 총 비용은 900달러이다.
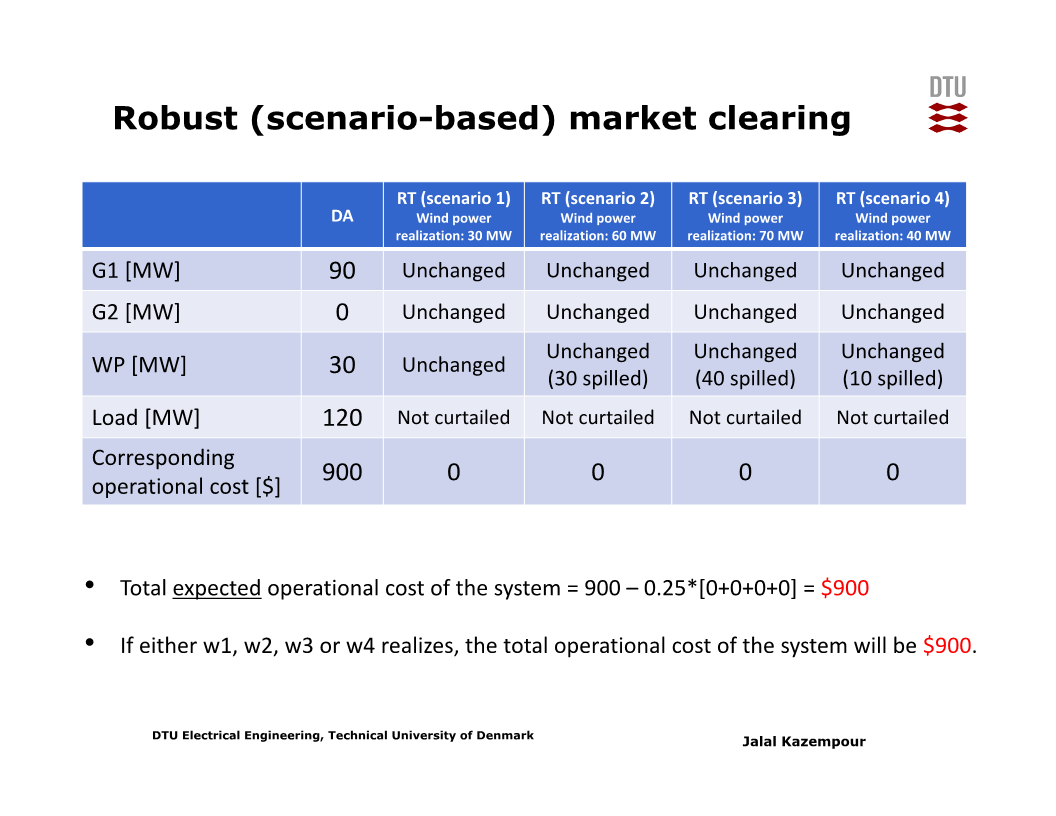
위 4개 시나리오들에 대해 stochastic market clearing 수행 시 총 비용의 ‘기대값’은 850달러로 robust market clearing에서의 비용보다 낮다.
그러나 stochastic market clearing 기반으로 하루전 시장에서의 급전계획을 도출 후 실시간 시장에서 worst-case가 발생할 경우 (실제 풍력발전량이 30MW인 경우) 의 총 비용은 1200달러이다. 즉, robust market clearing을 통해 ‘최악의 상황에서의’ 비용을 1200달러에서 900달러로 낮추었다.
Worst-case를 어떻게 찾는가?
사실 위 문제처럼 풍력 발전기의 출력이 0 이상 70MW 이하인 경우, 엄밀히는 0에서 70MW까지의 모든 시나리오를 고려할 필요가 있으며, worst-case는 풍력 발전기의 출력이 0인 상황이다.
만약 풍력 발전기가 한 대 더 있는 경우에도, worst-case는 두 풍력 발전기 모두의 출력이 0인 상황이다. 아래 슬라이드의 가로축은 풍력발전기 1의 출력, 세로축은 풍력발전기 2의 출력이다. 이 경우 원점이 worst-case임이 자명하다.
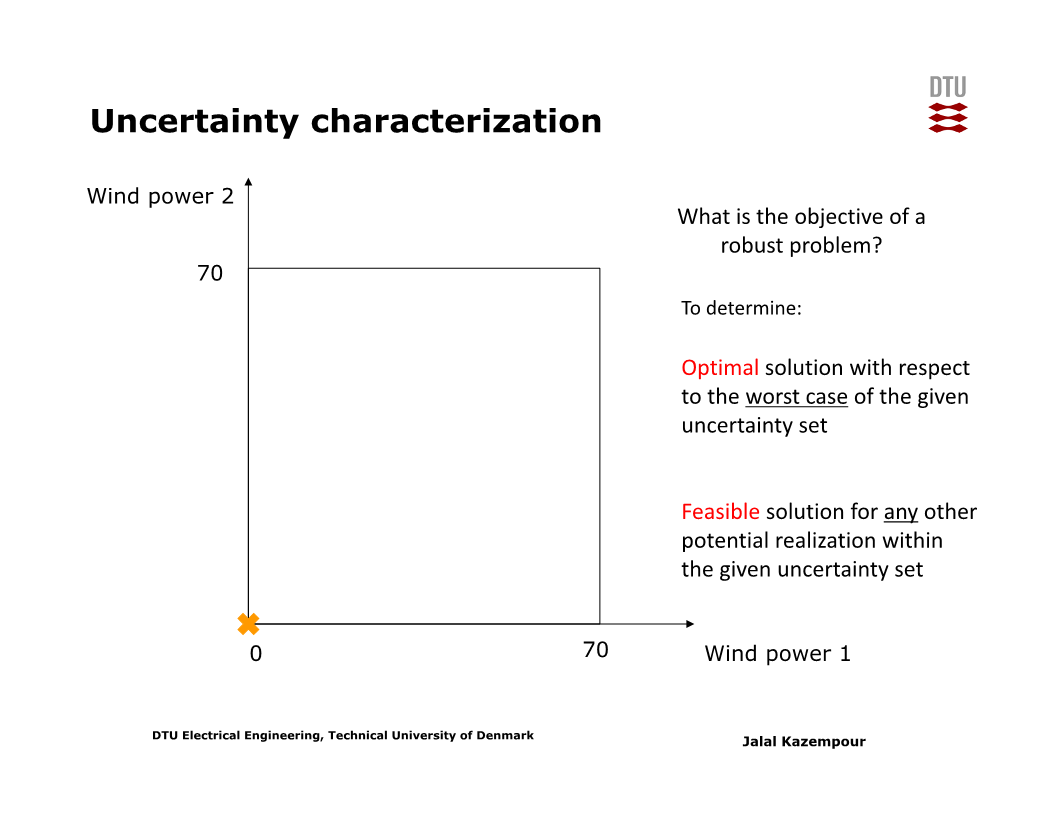
그리고 모든 풍력발전 출력 시나리오들은 ‘box’안에 있다. 이를 box uncertainty set이라 한다. Box uncertainty set에서는 worst-case가 꼭지점 중 하나이고 꼭지점 수가 적으므로 worst-case를 찾기 쉽다.
그러나 실제 적용 시, worst-case를 이렇게 직관적으로 찾을 수 없는 경우가 많다.
이를테면 여러 개의 발전원들을 다변화된 포트폴리오처럼 구성하여 ‘실질적으로는’ 모든 발전원의 출력이 0인 경우가 사실상 없다든지, correlation이 있어 위처럼 단순한 box 모양이 아니라 다면체 (polytope) 또는 타원 (ellipsoid) 꼴의 uncertainty set을 가진다든지 할 경우에는, worst-case를 직관적으로 찾을 수 없다.
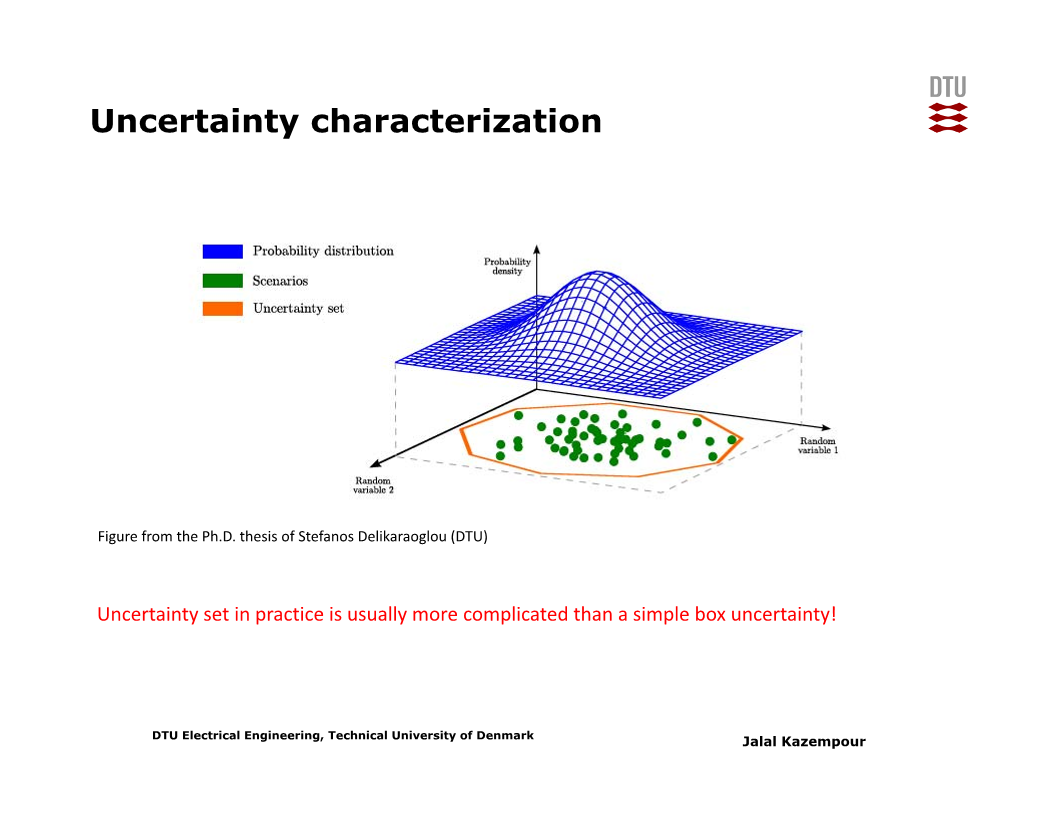
Uncertainty set을 수식으로 표현할 수 있을 경우, ‘시나리오를 쓰지 않고’ uncertainty set을 직접 최적화 문제에 명시하여 robust market clearing 문제를 구성할 수 있다.

위 문제에서의 uncertainty set 수식은 $ 0 \leq W \leq 70 $ 이다.
그런데 위 문제에서는 세 개의 최적화 문제가 계층적으로 (hierarchically) 중첩되어 있어 바로 풀 수 없다. 구체적으로는 min-max-min problem으로, 이를 풀기 위해서는 duality를 이용한 변환이 필요하다.
실시간 시장에 대한 최소화 문제를 inner problem이라 할 때, 이 inner problem의 dual problem은 최대화 문제이다. 그러므로 inner problem의 dual problem을 바로 바깥의 최대화 문제와 합칠 수 있다 (아래 두 슬라이드 참고).
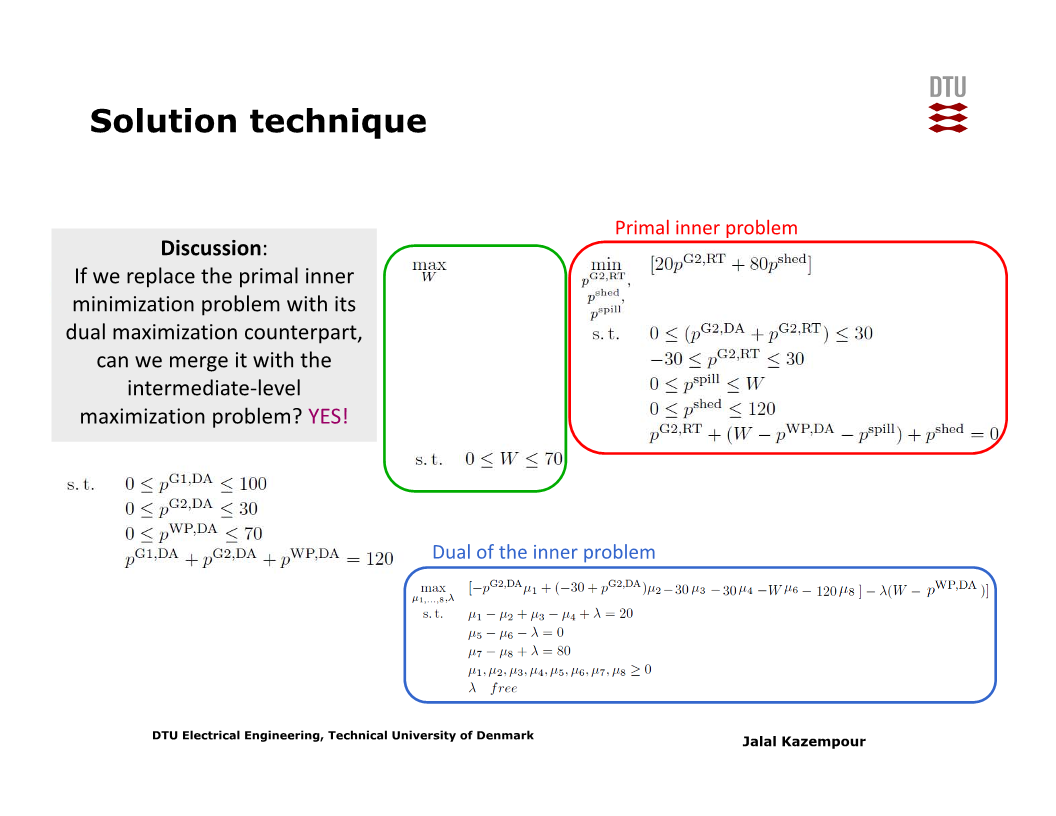

여기서 난점은, 합쳐진 문제의 목적함수에 $W$와 dual variable 간 곱 (product), 즉 nonlinear term이 포함된다는 것이다.
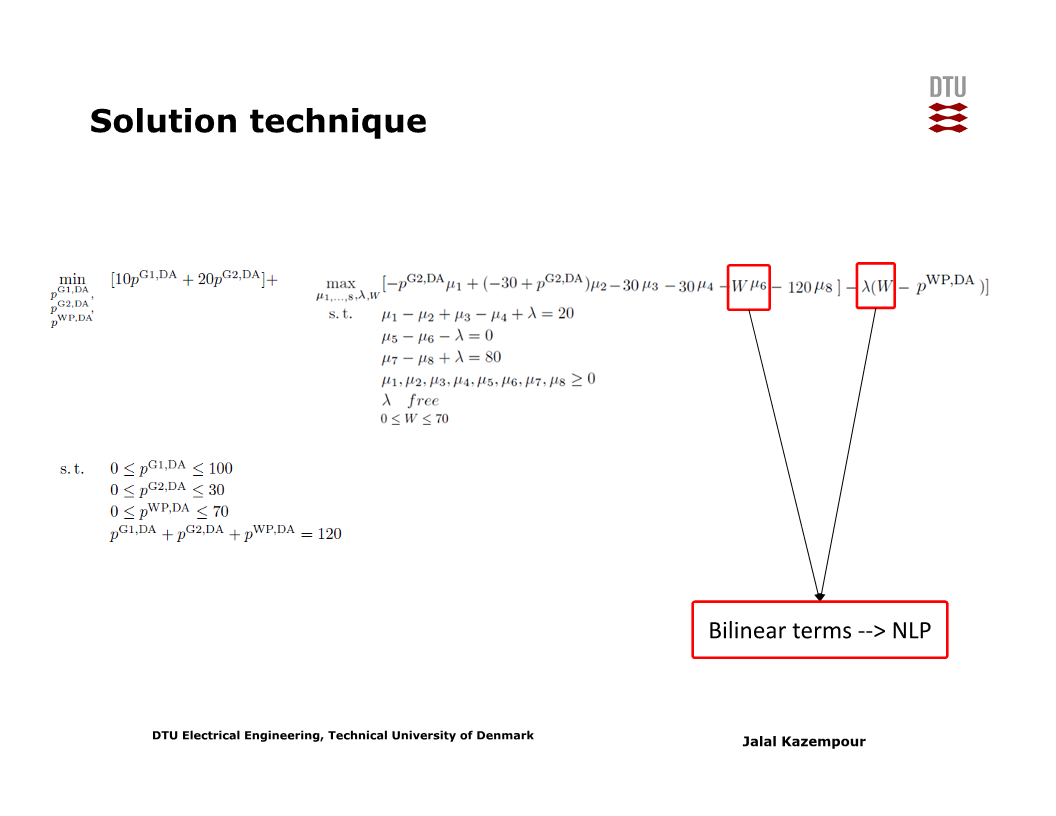
이 문제를 푸는 한 가지 방법은, $W$의 값을 uncertainty set의 꼭지점 (vertex)의 값으로 ‘고정’하는 것이다. 그러면 linear problem이 되므로 빠르게 풀 수 있다. 이러한 linear problem을 각 vertex 별로 풀어서 목적함수를 비교할 수 있다.
그러나 이는 vertex 수가 많으면 실행하기 어렵고, 실제로 vertex 수는 재생발전원 수에 지수적으로 (exponentially) 증가한다.
위에서 소개한 풍력발전기들에 대한 box uncertainty set을 예로 들면, 풍력발전기가 $N$개 있을 때 꼭지점 수는 $2^N$개이다. 그러므로 풍력발전기가 스무 개 정도만 넘어가도, 실질적으로 쓸 수 없는 방법이 된다.
만약 풍력발전기들 간의 correlation 등까지 고려해서 uncertainty set이 복잡한 모양을 갖게 되면 꼭지점 수는 더 증가할 것이다 (또는 uncertainty set이 타원형 등이어서 아예 vertex가 없을 수도 있다).
제약조건이 만족될 ‘확률’ 기반 문제 구성
Worst-case approach로 얻은 solution은 종종 지나치게 보수적이다 (conservative). 불확실성이 크더라도, 대개 worst-case보다는 나을 것이기 때문이다.
이를 완화하는 한 가지 방법으로, 각 제약조건들이 항상 충족되는 것이 아니라 100퍼센트보다 낮은 어떤 ‘확률’로 충족될 것을 조건으로 두는 chance-constrained programming이 있다.

Uncertainty $\Delta W$의 분포를 알고 있다고 가정하면 (최소한 충분한 데이터를 통해 근사 분포를 도출할 수 있다면), 위 제약조건이 충족될 확률도 계산 가능하다.
Chance-constraints를 market clearing에 적용한 문제는 아래와 같다.

여기서 $p^{G2.RT}$, $p^{shed}$, $p^{spill}$은 $\Delta W$의 ‘함수’ 임에 유의한다. 이들은 실제 풍력발전량이 얼마인가에 따라 달라지는 변수들이기 때문이다.
(여기서는 편의상 각각의 제약조건들이 ‘개별적으로’ $1 - \epsilon$의 확률로 충족된다고 하였으나, 실제로는 여러 제약조건들에 대한 ‘joint’ constraint가 필요할 수도 있다.)
그러면 이 chance-constraint problem을 실제로 풀려면, 어떻게 해야 하는가?
만약 uncertainty (위에서는 $\Delta W$) 의 분포가 정규분포인 case 등 특수한 몇몇 case에 해당한다면, analytical reformulation이 가능하다. 실제로 chance-constrained linear programming problem은 uncertainty가 정규분포라는 가정 하에 second-order cone programming (SOCP) problem으로 변환 가능함이 알려져 있다.
그러나 위처럼 analytical reformulation이 가능한 확률분포로 가정할 수 있는 경우는 그리 많지 않다. 특히 재생발전원의 경우 true data generating process가 복잡하므로, 더더욱 가능성이 떨어진다.
결국 확률분포로부터 sampling 수행 후 해당 sample들에 대해 제약조건이 만족된다는 조건을 설정하는 것이 현실적인 방안이다.
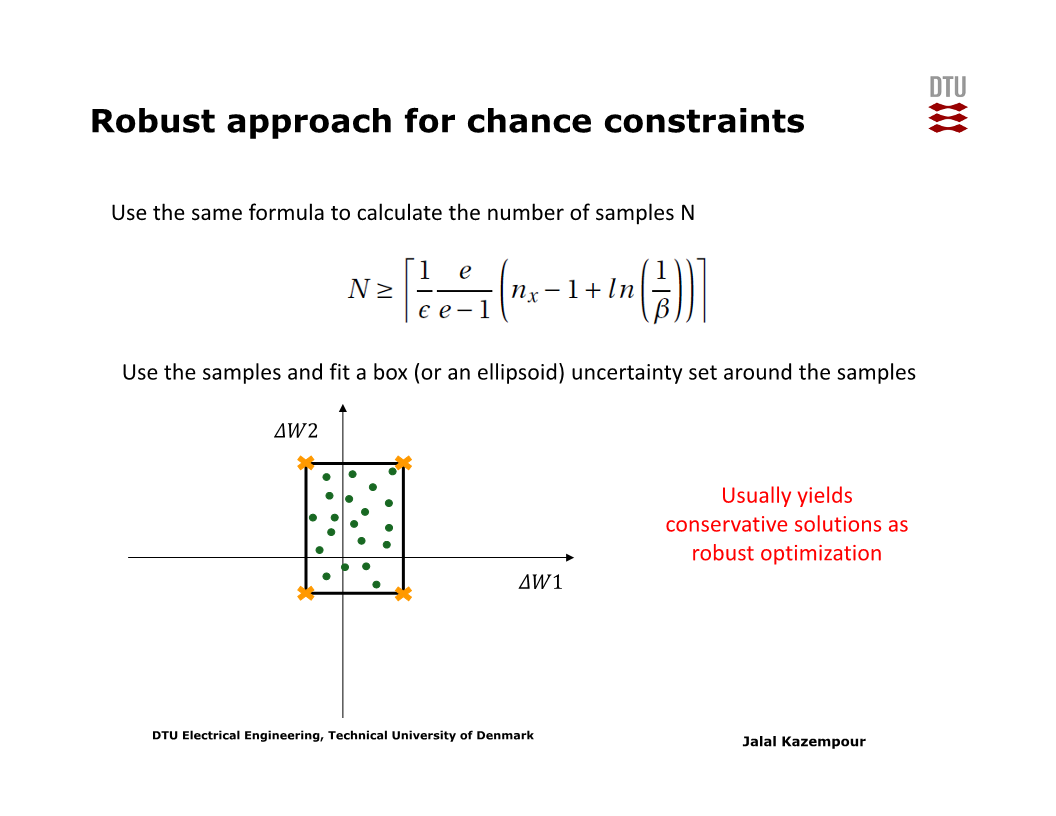
아래 슬라이드를 보면, 주어진 $\epsilon$ 및 문제 크기 $n_x$와 confidence level $\beta$에 대해, $N$개 이상의 sample들에 대한 제약조건을 걸면 사실상 chance-constraint가 충족됨이 알려져 있다.

그러나 이 $N$값은 대개 매우 크므로, 문제도 매우 커져 풀기 곤란해진다. (이후 강의들에서 설명할 decomposition techniques를 쓰면 풀 수도 있다.)

만약 uncertainty의 차원이 작은 편이라면, 아래 슬라이드처럼 ‘approximate’ box uncertainty set을 구성하고 해당 set의 vertex들에 대해 문제를 풀 수도 있다 (단, 이 경우 robust optimization이 되므로 보다 보수적인 해를 얻는다).
Uncertainty의 분포를 모른다면?
위에서 설명했던 chance-constraint problem은 uncertainty에 대한 분포를 필요로 했다. 그런데 실제로는 그 분포를 모른다.
이 경우 대안으로, ‘data generating process를 표현할 가능성이 있는 여러 개의 확률분포들’ 을 사용할 수 있다. 이러한 방법을 distributionally robust optimization (DRO) 라 한다.
실제 확률분포를 모르기 때문에 말 그대로 여러 개의 확률분포’들’을 사용하며, 해당 확률분포들의 집합을 ambiguity set이라 한다.

위 슬라이드에서 각 chance constraint는, ambiguity set 내의 모든 확률분포들 각각에 대해 해당 제약조건이 충족될 확률을 계산했을 때 그 중 ‘가장 낮은 확률’ 이 $1 - \epsilon$ 이상이 되어야 한다는 조건이다.
이 때 첫번째 chance constraint에 대해 충족 확률이 가장 낮은 (그러나 $1 - \epsilon$보다는 크거나 같은) 분포를 A라 하고, 두번째 chance constraint에 대해 충족 확률이 가장 낮은 분포를 B라 하면, A와 B는 서로 다를 수 있다.
Historic data가 있을 경우, ambiguity set을 구성하는 방법으로 크게 두 가지가 있다 (metric-based, moment-based)
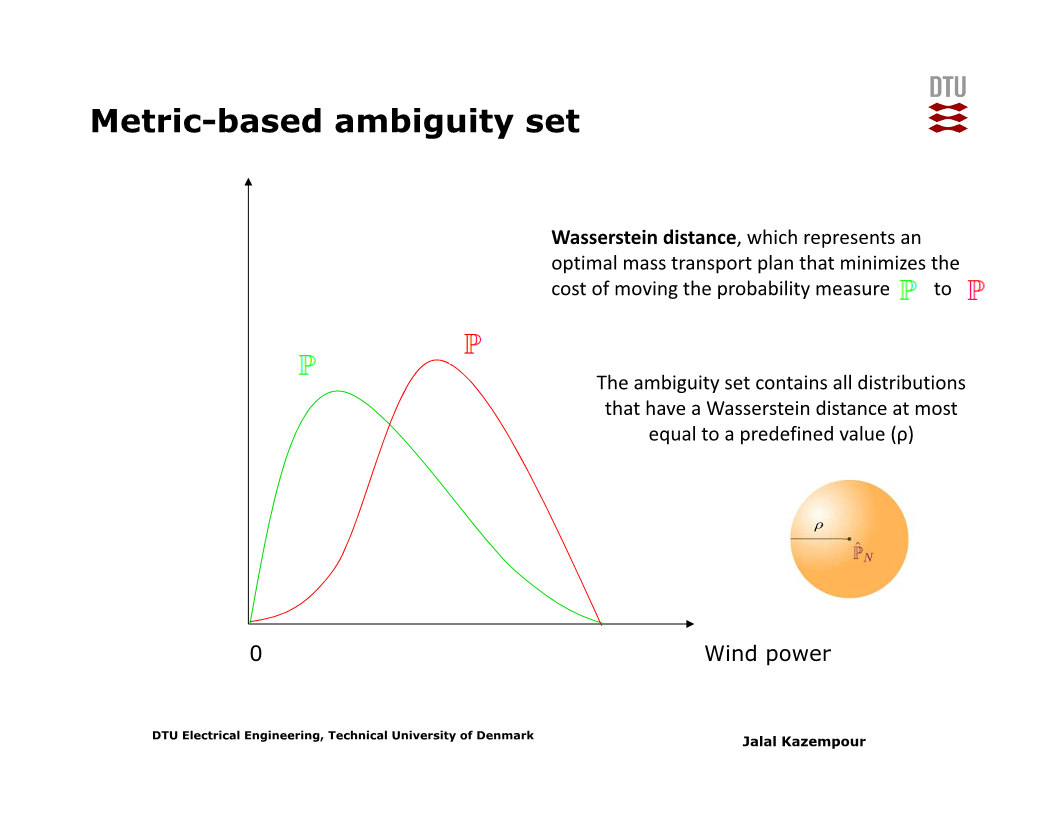
Metric-based 방법으로는, sample들로 구성된 empirical distribution과 차이가 일정 수준 이하인 분포들로 ambiguity set을 구성한다. 여기서 ‘차이’는 Wasserstein distance 등이 될 수 있다 (아래 슬라이드 참고)
Moment-based 방법으로는, sample들의 first moment와 second moment를 (+ 필요 시 higher moments를) 계산 후, 해당 moment condition을 갖는 모든 확률분포들로 ambiguity set을 구성한다.
01) Market clearing as an optimization problem
02) Market clearing as an equilibrium problem
03) Desirable properties of market-clearing mechanisms
04) Market clearing using a cooperative game approach
05) Stochastic market clearing
06) Robust approaches for market clearing
07) Bilevel programming in energy systems
08) Optimization problems with decomposable structure
09) Benders’ decomposition: Theory
10) Benders’ decomposition: Applications
11) Augmented Lagrangian relaxation
12) Variants of ADMM and applications