에너지시스템 최적화/게임이론 강의: 7) Bilevel programming in energy systems
이 포스팅은, Technical University of Denmark의 박사과정 과목 “Advanced Optimization and Game Theory for Energy Systems” (Prof. Jalal Kazempour) 의 7강을 필자가 요약한 내용이다.
발전사업자가 ‘정직하지 않을’ 경우의 시장
지금까지의 강의들에서는 모든 발전사업자가 자기 소유 발전기의 발전비용 (production cost) 을 offer price로써 ‘정직하게’ 설정한다고 가정했다. 그리고 이 때 social welfare가 최대화됨을 보였다.
그러나 만약에, 가격 결정의 key를 쥐고 있는 ‘marginal’ producer (수요-공급 일치점에 해당하여 자신의 offer price가 곧 market clearing price가 되는 공급자) 가 offer price를 production cost보다 높게 설정하는 ‘strategic’ offering을 했다고 하자. (이를 exercising market power 라 한다)
그 결과, market clearing price는 증가하고, 전체 전력 공급량은 감소한다 (아래 슬라이드 참고).
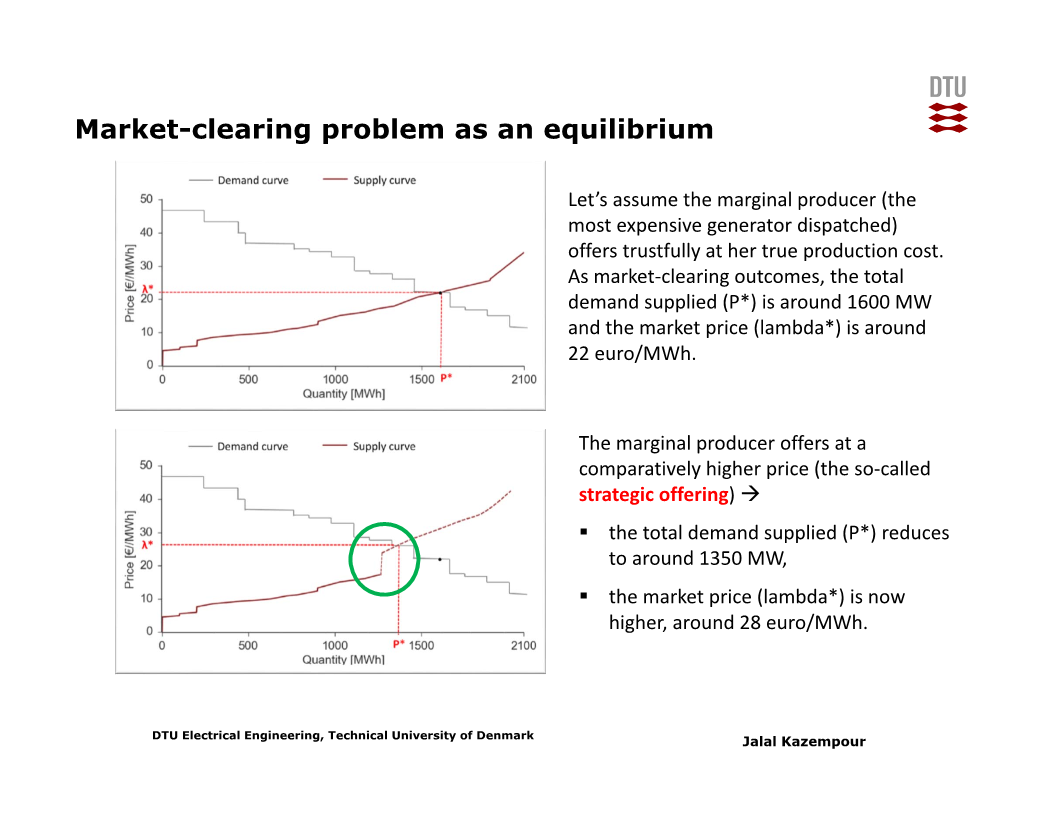
이 때, marginal producer의 수익은 증가할까?
이는 marginal producer의 판매량에 따라 다르다. 판매가격은 증가했지만, 전체 전력 공급량은 감소했다. 만약 전력 공급량 감소에 의해 marginal producer의 판매량이 크게 감소하면, marginal producer의 수익은 감소할 수도 있다. (물론 실제로는 marginal producer도 이를 예상하고 본인의 수익이 증가할 것 같을 때에만 strategic offering을 수행할 것이다)
Marginal producer를 제외한 나머지 (전력수급 스케줄에 포함된) 발전사업자들의 수익은 증가한다. 판매량은 변하지 않는데 시장가격이 올랐기 때문이다. (일종의 free-rider로 볼 수 있다)
또한 startegic offering의 결과, social welfare는 감소한다 (아래 슬라이드 참고).
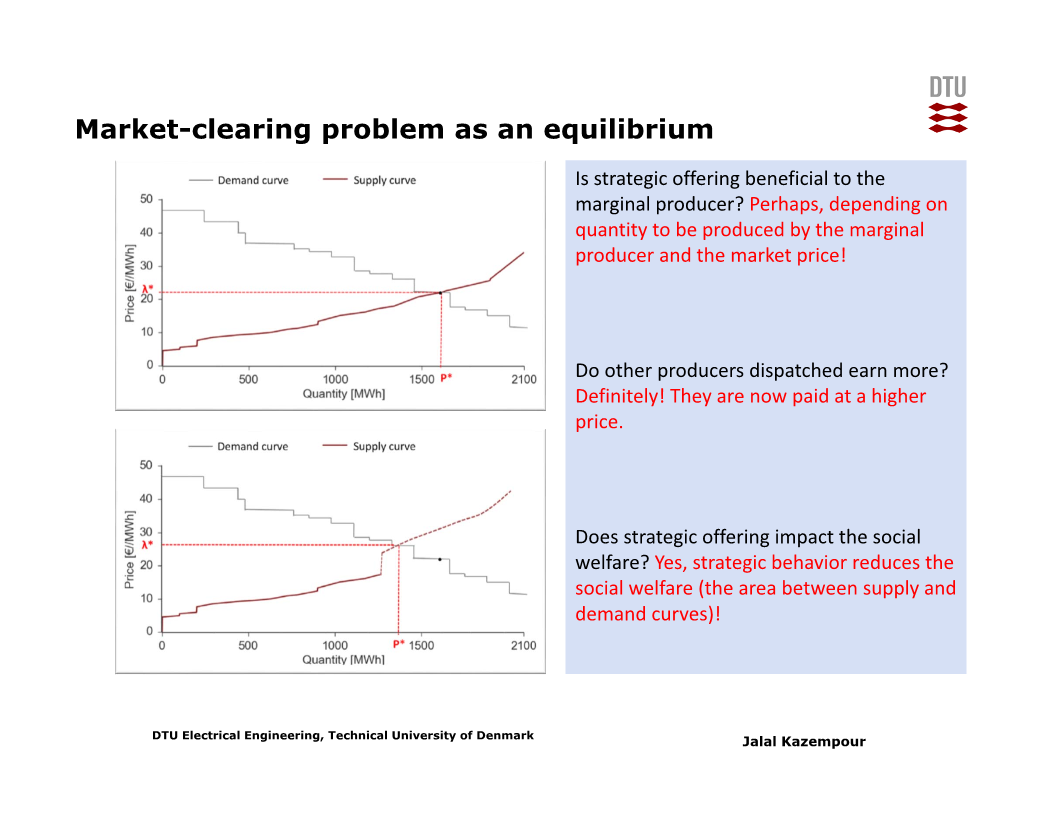
3강에서 보았듯 LMP-based market은 incentive compatibility가 충족되지 않는 시장이므로, 각 참여자들이 자신의 진짜 정보가 아닌 가짜 정보를 이용할 위험이 있다.
Strategic offering을 Stackelberg game으로 모델링
시장은 근본적으로 여러 참가자들이 각자의 이익 최대화를 목표로 하는 상호작용 공간이므로, game으로 모델링할 수 있다. 실제로 생산량 기반 경쟁을 모사하는 Cournot competition, 가격 기반 경쟁을 모사하는 Bertrand competition, 이들 모델보다 더 전력시장의 모습에 가까운 supply function model 등이 사용될 수 있다.
그러나 위 모델들은 기본적으로 ‘생산량과 가격 간 관계가 affine function이다’ 라고 전제하는데, 실제로는 그렇지 않다. 그러므로 이러한 전제를 필요로 하지 않는 다른 game 모델이 필요하다.
Strategic offering을 하는 발전사업자가 자신의 offer price를 결정하면, market operator는 해당 offer price를 ‘주어진 것으로 받아들이고’ market clearing을 수행한다.
그러므로 strategic offering을 하는 발전사업자를 leader로, market opeartor를 follower로 보면, 전형적인 Stackelberg game이 된다.
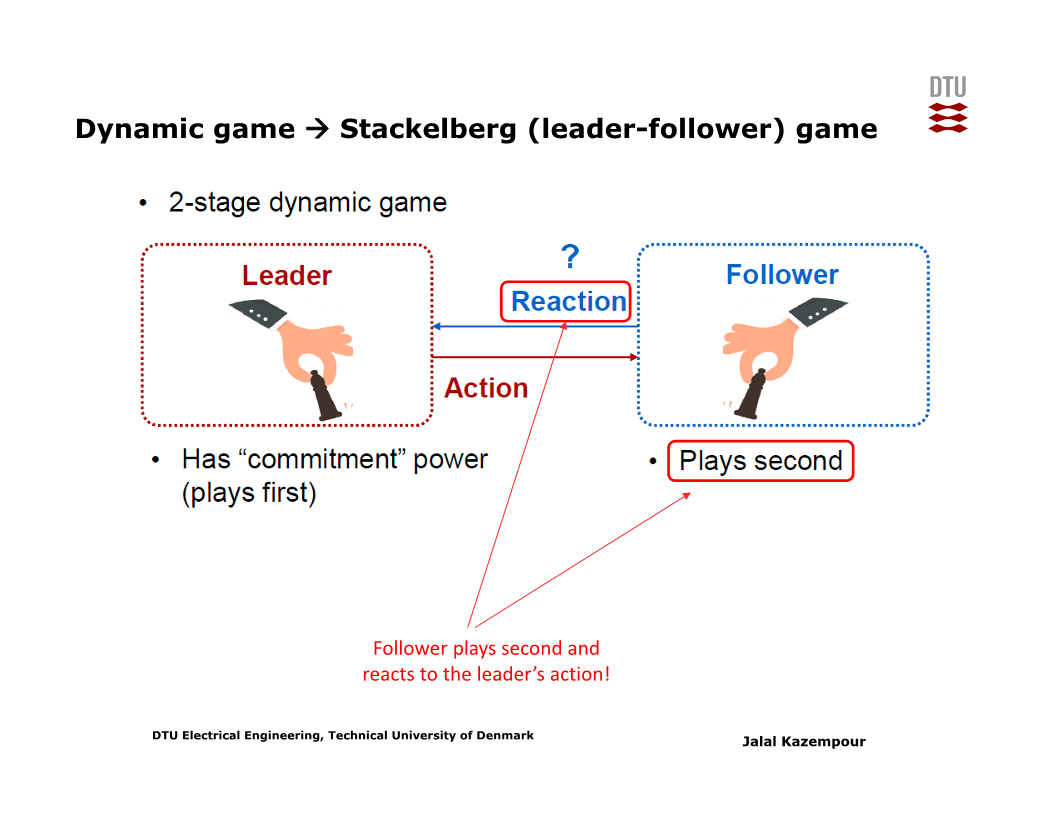
Stackelberg game에서는 leader가 follower의 모델을 알고 있다고 가정하고, leader가 follower의 model에 기반해 자신의 선택에 대한 follower의 대응을 ‘예상해서’ 의사결정을 한다.
그러므로, leader의 의사결정에 대한 최적화 문제는 leader 자신에 대한 제약조건 뿐 아니라, follower의 의사결정에 대한 최적화 문제 자체를 제약조건으로 갖는 bi-level problem이 된다 (아래 슬라이드 참고).
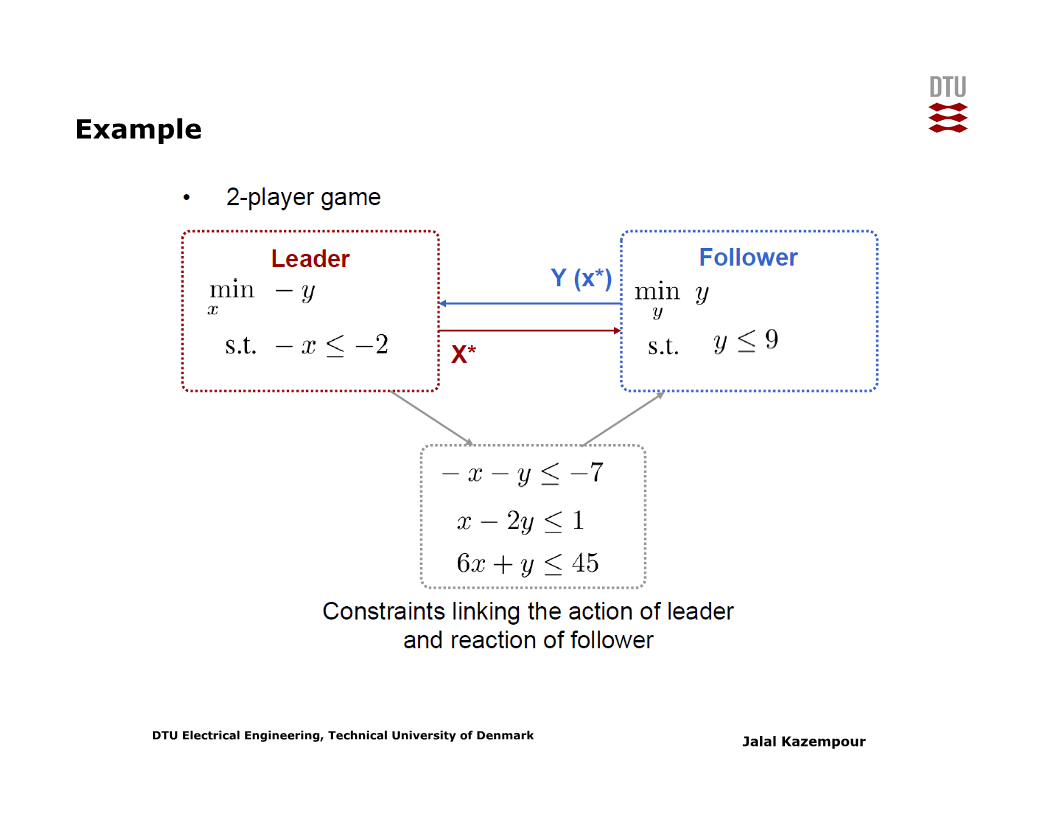
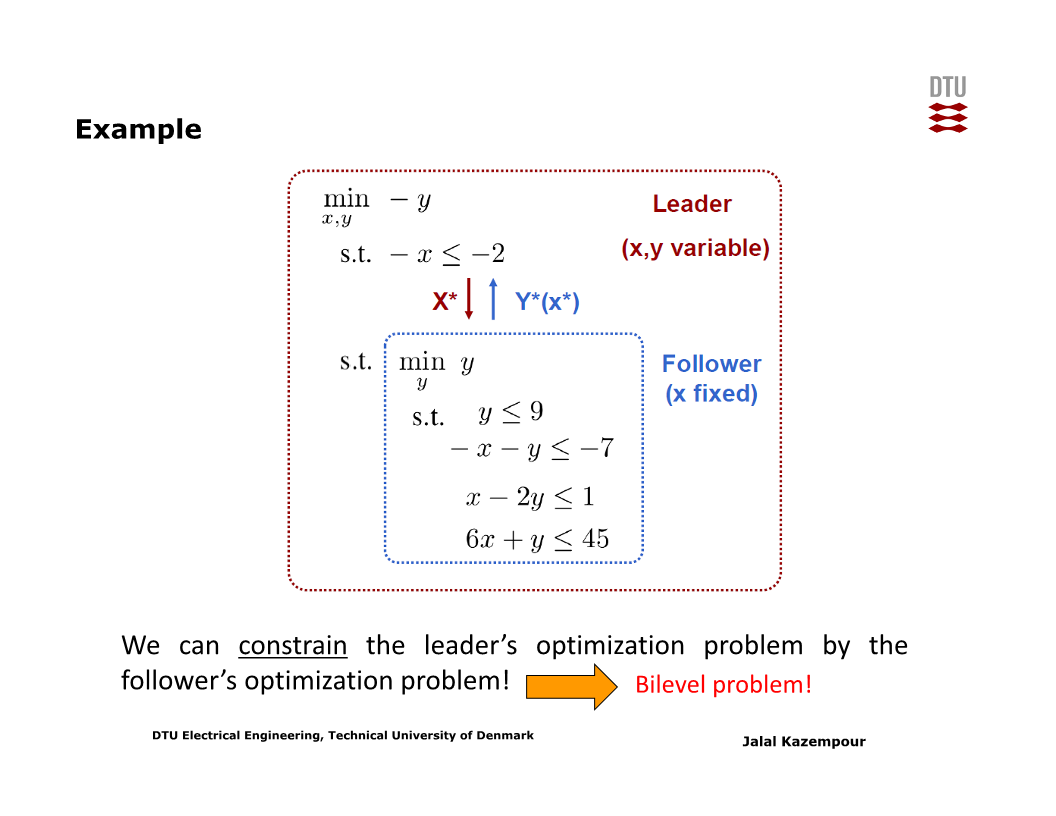
Follower 입장에서의 lower-level problem에서는 leader의 의사결정이 변수가 아닌 parameter이다. Leader 입장에서의 upper-level problem에서는 leader의 의사결정과 follower의 의사결정 모두가 변수이지만, follower의 의사결정은 lower-level problem을 전제로 이루어진다.
Stackelberg game bi-level problem을 푸는 방법
Bi-level problem을 푸는 일반적인 방법은, lower-level problem의 KKT condition을 upper-level problem의 제약조건으로 두는 것이다. Optimal point에서는 lower problem의 KKT condition도 만족되어야 하기 때문이다. 이 경우, 최적화 문제를 제약으로 갖지 않는 평범한(?) 최적화 문제가 된다.
(이러한 문제를 Mathematical Program with Complementarity Constraint (MPCC) problem이라 하며, 특히 전력시장처럼 lower-level problem이 equilibrium을 구하는 문제인 경우에는 Mathmatical Program with Equilibrium Constraint (MPEC) problem이라 한다.)
여기서 난점은, KKT condition 중 complementary slackness 조건에 의해 lower-level problem의 primal variable들과 dual variable들이 곱해져 product term들이 생기므로 nonlinear problem이 된다는 것이다.
이 때 각 product term에 대해 이진변수와 큰 계수 기반의 big-M approach를 쓰면, mixed-integer ‘linear’ problem으로 만들 수 있다 (아래 슬라이드 참고).

이제 strategic offering을 모사하는 최적화 문제를 보자. Bi-level problem은 아래 슬라이드와 같다.
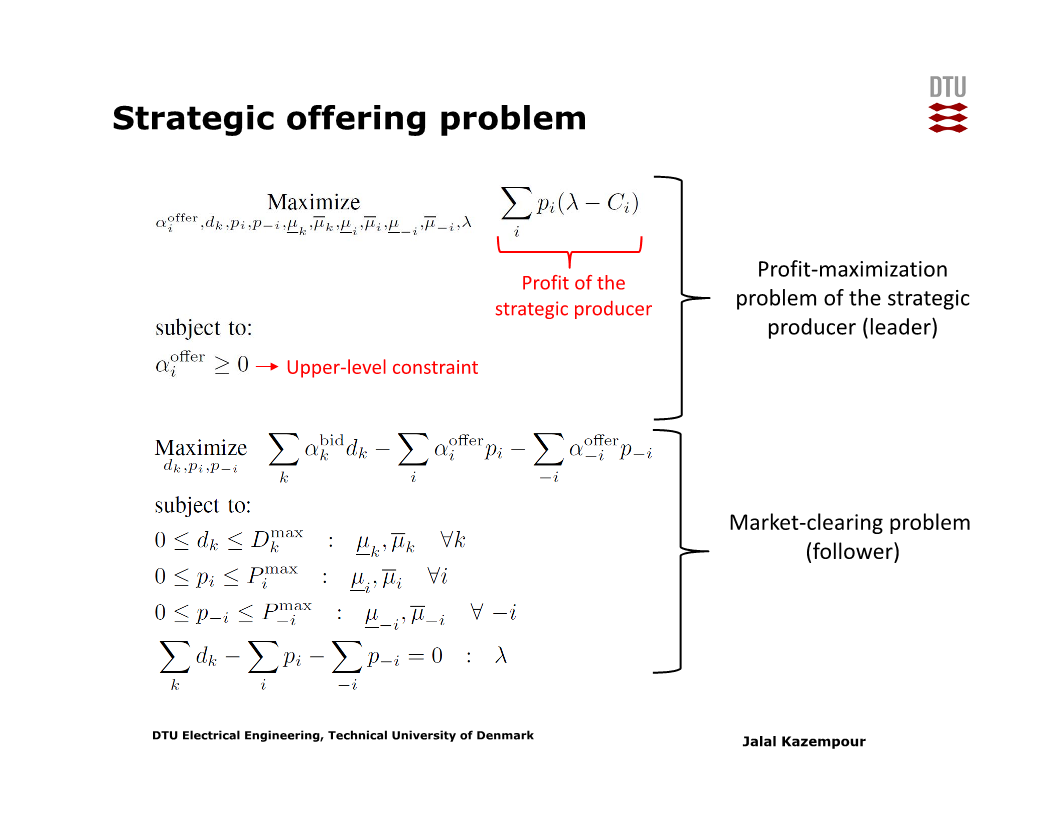
Market operator에 대한 lower-level problem의 KKT condition들을 도출하고 이를 big-M approach를 써서 이진변수 기반 선형 조건들로 변환한 문제는 아래 슬라이드와 같다.

여기서 또다른 난점이 있다. 목적함수에 있는 $p_i \lambda$ 항이 nonlinear term이란 것이다. $p_i$는 발전사업자의 판매량이고 $\lambda$는 가격인데, 둘 다 변수이기 때문이다.
Mixed-integer ‘non’linear programming problem은 어떤 상용 solver로도 쉽게 풀 수 없는, 대단히 어려운 문제이다. 따라서 이를 동치인 선형 문제로 변환할 필요가 있으며, 다행히 이 문제에서는 변환이 가능하다.
아래 슬라이드가, $\sum_i p_i \lambda$ 항을 동치인 linear term들로 표현하는 과정이다.
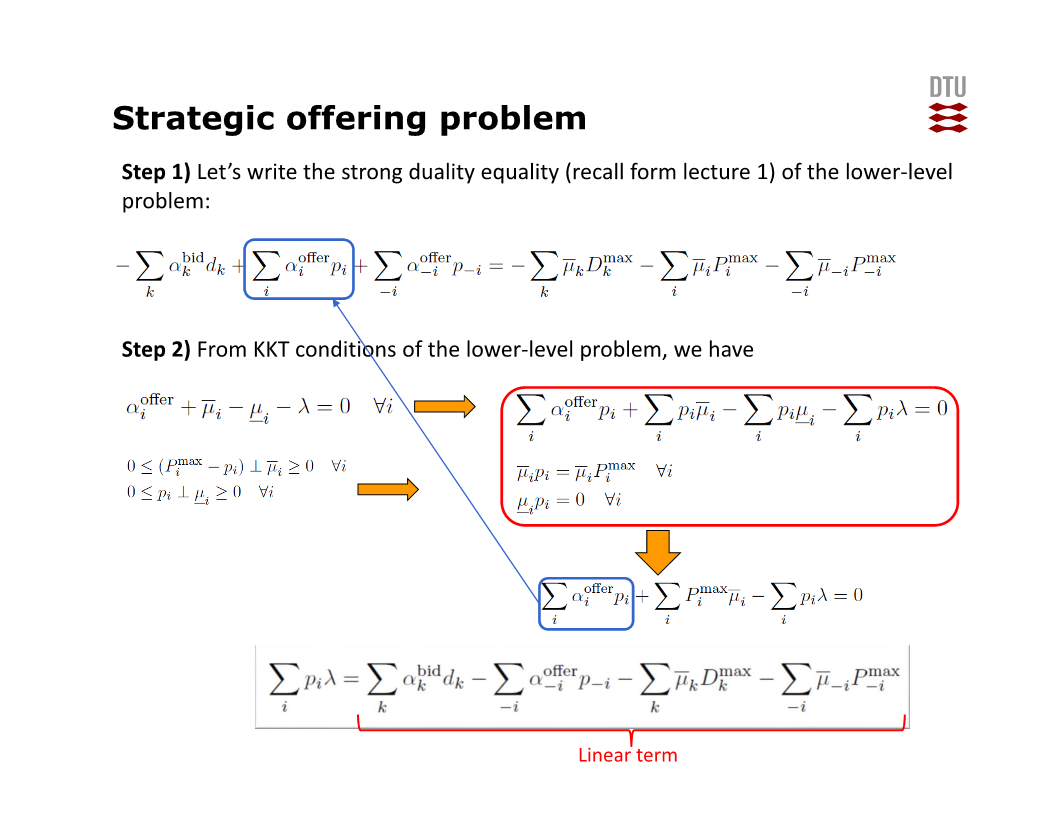
Lower-level problem은 linear programming problem이므로 항상 strong duailty가 성립한다. 그러므로 step 1에서는 primal objective와 dual objective 간의 등식을 쓴다.
Step 2에서는 KKT condition의 zero first derivative 조건들 중 $\lambda$가 있는 조건을 쓰고, 여기에 $p_i$를 곱한 후 $i$에 대해 합한다. 그러면 step 1의 식을 대입해서, $\sum_i p_i \lambda$ 항을 동치인 linear term들로 표현할 수 있다.
최종적인 mixed-integer ‘linear’ programming problem은 아래와 같다.

‘여러 명이’ strategic offering을 하는 경우는?
위 내용들은 모두 ‘한 명의 발전사업자가’ strategic offering을 수행하는 경우의 MPEC problem에 대한 설명이었다.
그러나 실제 시장에서는, strategic offering을 할 유인이 있는 발전사업자들이 여러 명일 것이다. 그리고 여러 명이 strategic offering 수행 시에도, 나름대로의 ‘균형’ 상태에서 market clearing이 이루어질 것이다.
이러한 문제를 Equilibrium Problem with Equilbrium Constraints (EPEC) problem이라 하며, 이는 상당히 풀기 어려운 문제이다. 문제 자체의 크기도 클 뿐 아니라, 수렴이 보장되지 않고, 수렴하더라도 해당 해가 균형이 아닐 수 있는 등 여러 가지 이슈가 있다.
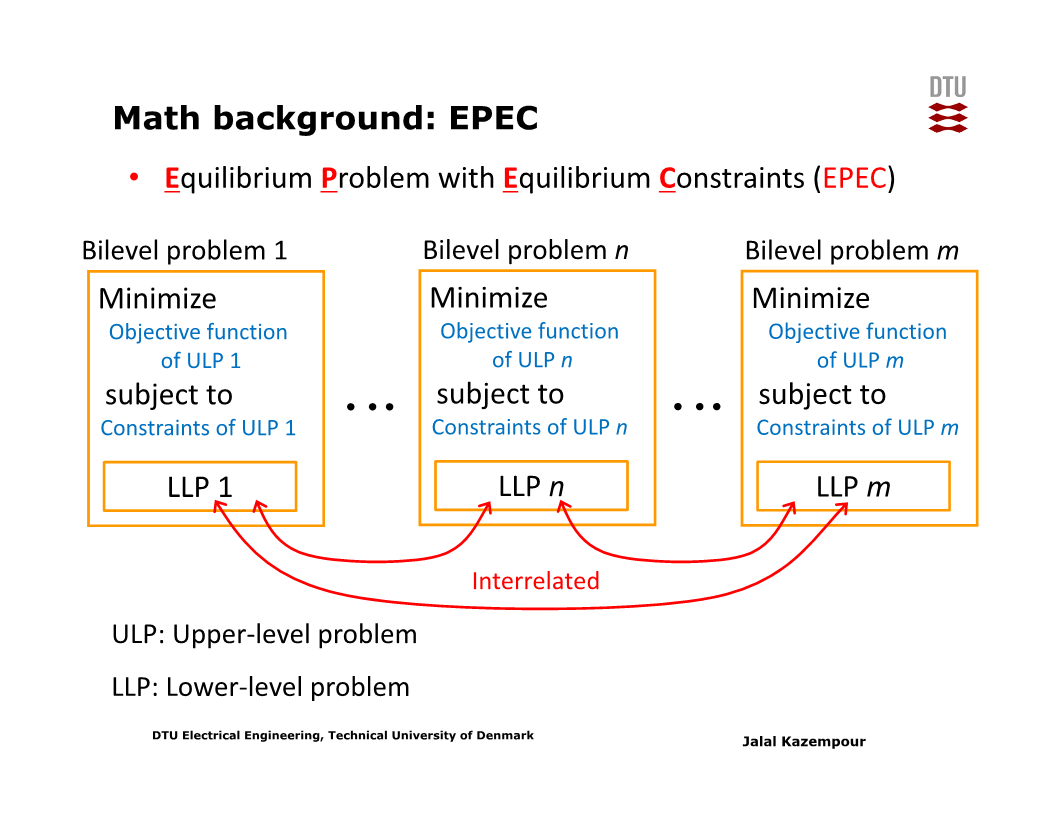
01) Market clearing as an optimization problem
02) Market clearing as an equilibrium problem
03) Desirable properties of market-clearing mechanisms
04) Market clearing using a cooperative game approach
05) Stochastic market clearing
06) Robust approaches for market clearing
07) Bilevel programming in energy systems
08) Optimization problems with decomposable structure
09) Benders’ decomposition: Theory
10) Benders’ decomposition: Applications
11) Augmented Lagrangian relaxation
12) Variants of ADMM and applications