에너지시스템 최적화/게임이론 강의: 10) Applications of Bender’s decomposition
이 포스팅은, Technical University of Denmark의 박사과정 과목 “Advanced Optimization and Game Theory for Energy Systems” (Prof. Jalal Kazempour) 의 10강을 필자가 요약한 내용이다.
Generation expansion planning
아래 문제는 기존 두 개의 발전기에 더해 새로 도입되는 세 번째 발전기의 용량 $x_3$을 결정하되, 각 시간별 수요-공급 일치 및 발전기 별 운전 범위 조건을 만족시키면서 ‘발전기 건설비와 모든 시간의 운영비용의 합’을 최소화하도록 결정하는 설비 확장 (generation expansion) 문제이다.

$x_3$의 값을 고정하면, 각 시간 ($h$) 별로 subproblem을 구성할 수 있다. 주어진 $x_3$에 대해 각 시간 별 발전기들의 최적 출력을 결정하는 subproblem은 아래와 같다.

Master problem의 optimality cut을 compact form으로 구성하기 위해, $x_3^{(i)}$을 변수로 두되 해당 변수의 값을 고정하는 제약조건 $x_3^{(i)} = x_3^{fixed}$ 를 두었다. 해당 제약에 대응하는 dual variable $\lambda_h$가 $h$별로 다른데, 이는 각 시간 별 전기부하 $D_h$가 얼마냐에 따라 optimal solution이 달라지므로 dual variable도 $h$별로 다르기 때문이다.
$x_3$의 값을 업데이트하기 위한 master problem은 아래와 같다.

$\alpha^{(i)}$에 대한 제약조건의 우변이 모든 $h$에 대한 합임에 주의한다. $\alpha^{(i)}$가 목적함수의 $x$를 제외한 변수들에 대한 항들을 대신하는 auxiliary variable인데, 해당 항들은 ‘모든 시간에 대한 운영비용의 합’이기 때문이다.
또한 제약조건이 총 $i-1$개임에 주의한다 (1번째, 2번째, …, $i-1$번째 iteration에서의 값들)
Scenario based stochastic programming
불확실성이 큰 재생발전기가 있을 때, 하루전 시장에 대해서는 재생발전기 발전량 시나리오에 관계없이 단일한 급전계획을 도출하고, 실시간 시장에 대해서는 각 시나리오 별 급전 수정 계획을 도출함을 이전 강의에서 설명하였다.
아래 슬라이드를 보면, stochastic market clearing problem에서 complicating variables는 하루전 (Day-Ahead) 시장에 대한 변수들이고 (파란색으로 표기됨), 해당 변수들을 고정하면 각 시나리오 별 subproblem들을 구성할 수 있다.

각 시나리오 별 subproblem은 아래와 같다.

목적함수를 보면 0.25가 곱해져 있다. 이는 해당 시나리오의 확률이다. 각 subproblem별 목적함수에는 대응하는 시나리오의 확률을 곱해주도록 한다.
Master problem은 아래와 같다.

여기서 주의할 점은, $\alpha^{(\theta)}$에 대한 제약조건의 우변에서, subproblem의 목적함수에 대응하는 부분에는 각 시나리오 별 확률을 곱해주지만, 그 뒤의 complicating variable들에 대한 부분에는 각 시나리오별 확률을 곱해주지 않는다는 것이다.
이는 subproblem의 목적함수에 이미 각 시나리오 별 확률이 곱해져 있었기 때문에, complicating variable을 고정하는 제약에 대한 dual variable들 $\rho$가 ‘시나리오 별 확률만큼 scaling된’ sensitivity를 의미하기 때문이다. 그러므로 dual variable들을 전부 합하기만 해도, 각 시나리오 별 확률을 가중치로 하는 가중평균 sensitivity를 반영한 optimality cut을 생성하는 셈이 된다.
위의 4개 시나리오에 대한 stochastic market clearing 문제를 Bender’s decomposition으로 풀면, 아래와 같이 5번의 iteartion으로 해를 얻는다.
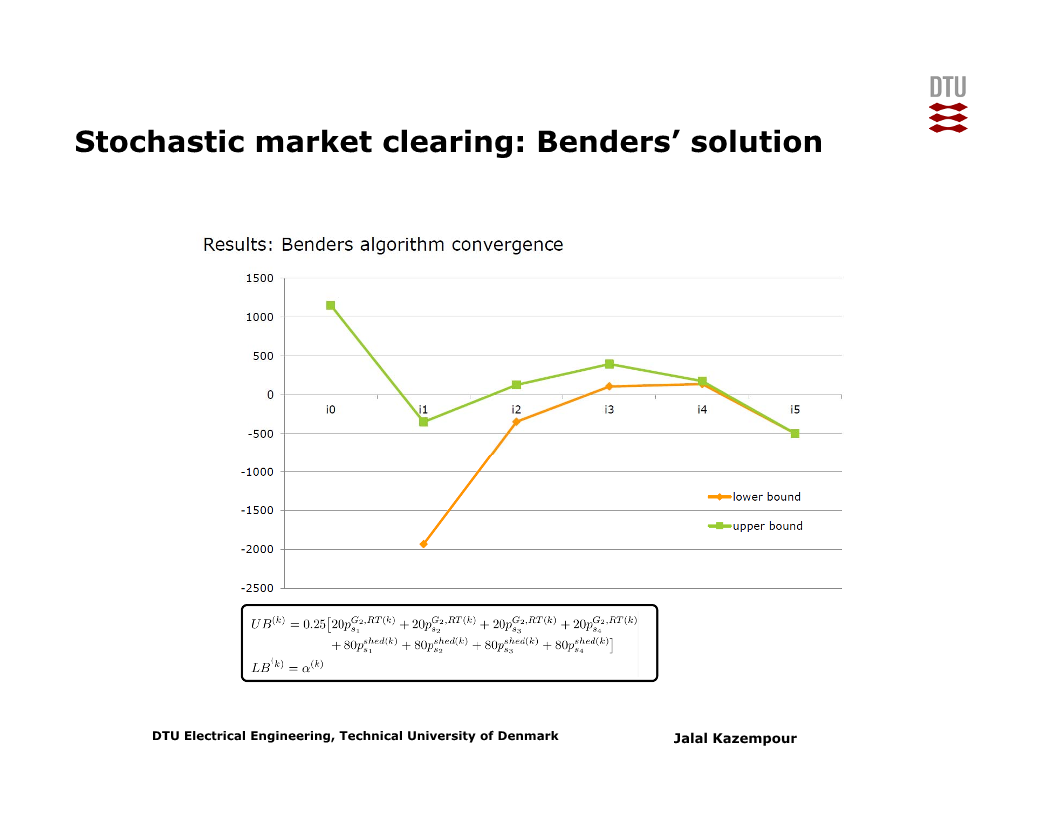
정수 변수가 있을 경우에는?
에너지시스템 최적화 문제에는 정수가 많이 등장한다. 설비규모 변수가 용량 자체가 아닌 기기 숫자일 수 있고 (풍력터빈이 몇 대이냐 등), 각 시간별 subproblem을 기동/정지 여부를 나타내는 이진변수를 포함하는 unit commitment 문제로 고려해야 할 수도 있다.
만약 Master problem에는 정수 변수가 있지만 subproblem들에는 정수 변수가 없을 경우, Bender’s decomposition을 적용할 수는 있다. 단, 이 경우 global optimum으로의 수렴이 보장되지 않음에 주의한다.
만약 subproblem에 정수 변수가 있으면, 안타깝게도 Bender’s decomposition을 적용할 수 ‘없다’. 정수 변수가 포함된 문제를 풀 경우 dual variable을 계산할 수 없어, master problem에서 complicating variable의 sensitivity 기반의 optimality cut을 생성할 수 없기 때문이다.
(필자도 개인적으로 관심을 갖는 주제 중 하나가 ‘unit commitment 제약을 고려한’ generation expanstion planning problem 풀이라서, 처음 이 사실을 알았을 때 좀 슬펐(?)다.)
이러한 경우 사용할 수 있는 방법론으로 primal-Benders, Dantzig-Wolfe decomposition 등이 있다고 알려져 있으나, 매우 복잡한 방법들이다.
현실적으로는 unit commitment 제약들을 ‘정수만 실수로 바꾸어서’ 구성한 문제를 풀어 용량변수의 값들을 도출 후, 해당 용량변수를 고정하고 일정 기간 (24시간 또는 48시간 정도) 동안의 unit commitment problem을 rolling 방식으로 푸는 것이 그나마 가능성 있는 방법으로 보인다. (단, 이 경우 용량변수의 값이 optimistic하게 계산되므로, 혹시라도 subproblem이 infeasible problem이 될 수 있으니 주의해야 한다.)
01) Market clearing as an optimization problem
02) Market clearing as an equilibrium problem
03) Desirable properties of market-clearing mechanisms
04) Market clearing using a cooperative game approach
05) Stochastic market clearing
06) Robust approaches for market clearing
07) Bilevel programming in energy systems
08) Optimization problems with decomposable structure
09) Benders’ decomposition: Theory
10) Benders’ decomposition: Applications
11) Augmented Lagrangian relaxation
12) Variants of ADMM and applications