강화학습 기반 마이크로그리드 control - 1) 미래를 모를 때의 ‘경제적’ control을 위한 강화학습
재생 발전의 비중이 커질수록, 당장 몇 시간 뒤의 발전량 및 순 부하 (재생발전량을 제한 net power load) 예측조차도 어려워진다. 이런 상황에서 과거 데이터들을 잘 이용해서 ‘경제적으로’ 전력을 공급하도록 설비들을 control하는 것이, ‘스마트’그리드의 중요한 과제이다.
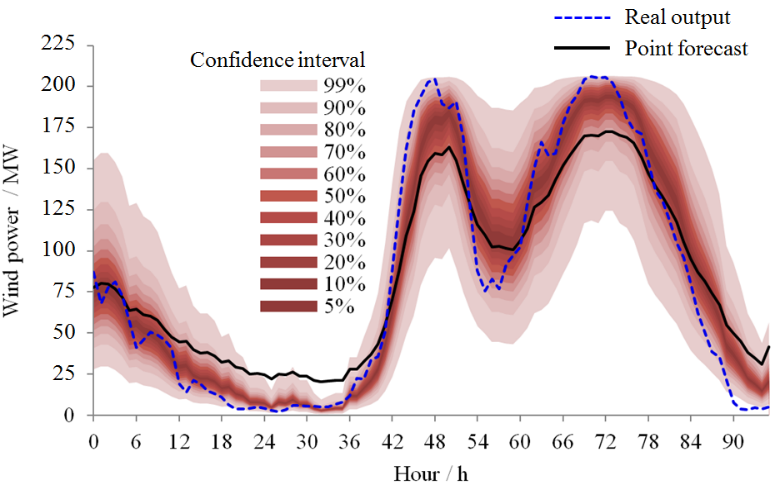 풍력발전 예측 시의 신뢰구간이 큼. 즉, 재생발전 비중이 높으면 발전량의 단기적 예측도 어려움.
풍력발전 예측 시의 신뢰구간이 큼. 즉, 재생발전 비중이 높으면 발전량의 단기적 예측도 어려움.
(출처: http://www.ningzhang.net/Renewables.html)
선형계획법의 한계: 미래를 안다고 가정 (비현실적)
이 블로그의 ‘Optimal System’ 카테고리에, 필자가 선형계획법 기반의 최적 에너지시스템 구성 및 스케줄링 도출을 설명했으며 해당 내용에는 태양광/ 풍력 등 재생발전 비중이 높은 시스템 대상 분석도 포함되어 있다.
그런데 선형계획법 기반 에너지시스템 스케줄링에서는, ‘미래’의 발전량과 부하를 ‘정확히 알 경우의’ control을 도출한다는 한계점이 있다 (실제로는 미래를 정확히 알 수 없음에도).
최적화 문제의 변수들이 각 시간별 수전/ 충전/ 방전 등이라 할 때, 해당 문제의 제약조건들로 ‘모든 시간에 대한’ 에너지 밸런스 제약이 포함된 상태에서 최적화를 수행하기 때문이다.
예시를 하나 들자. Vincent의 Liege 대학 박사학위논문 ‘Contributions to deep reinforcement learning and its applications in smartgrids’ 에서 연구대상으로 삼은 가상의 마이크로그리드 시스템은 아래와 같다.
최대부하 2kW 수준의 전기부하가 있으며, 이 부하에 전력을 공급하는 수단으로는 정격출력 12kW급 태양광 패널, 실용량 15kWh급 배터리 (충방전 효율은 80%), 그리고 부하에 연결된 수소연료전지 기반 중앙 계통이 있다.
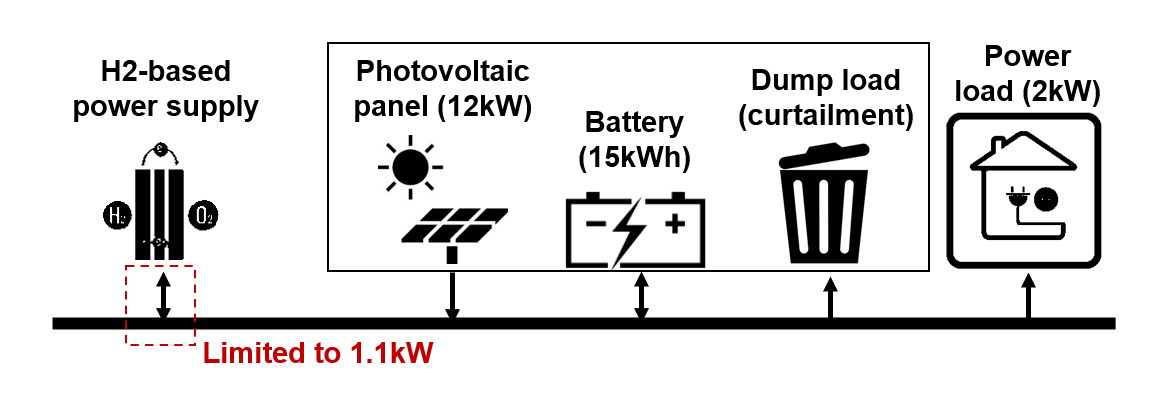 Vincent의 연구에서 가정된 마이크로그리드.
Vincent의 연구에서 가정된 마이크로그리드.
태양광 발전량이 부족할 경우 중앙 수소연료전지 시스템으로부터 전기를 받을 수 있다 (수전). 또는 태양광 발전량이 수요를 초과할 경우 전기를 역송해서 중앙 수소연료전지 시스템이 그린수소를 생산하도록 할 수 있다.
이 문제에서는 특이하게도, 계통 사이에 오갈 수 있는 전력이 1.1kW로 제한되어 있다 (개인적으로 일반적인 case는 아니라는 생각이 들지만… 일단 받아들이자).
이때 계통으로부터 전력을 받는 데 드는 비용은 해당 전기에너지 생산에 필요한 양만큼의 수소의 가격, 계통으로 잉여전력을 보낼 때의 수익은 해당 전기에너지로 만들 수 있는 양만큼의 수소의 가격이다.
이 논문의 가정에서는 수소 에너지 기준으로 1kWh 당 0.1유로이며 수소-전기 간 변환효율은 65%이므로, 보낼 때의 수익은 약 0.065유로/kWh, 받을 때의 비용은 약 0.154유로/kWh이다. 즉 역송 시의 수익이 수전 시의 비용보다 더 적다.
만약 태양광발전이 없고 배터리도 완방되어 있고 계통으로부터 1.1kW를 수전받음에도 부하를 충당하지 못할 경우, loss of load에 대한 큰 penalty성 비용 2.0유로/kWh가 발생한다 (부하 공급 실패에 대한 penalty를 큰 비용으로 환산함).
그러므로 특정 시간에 잉여전력이 많더라도, 이를 전부 송전해서 수소 가격만큼의 수익을 내려다가 나중에 태양광 발전량이 부족해지면 큰 손실을 볼 수 있다. 그러므로 배터리 내 에너지 저장량을 ‘적절히’ 유지해야 한다.
만약 잉여 태양광전력이 너무 많아서 배터리 완충 + 계통으로 1.1kW 송전 시에도 전력이 남으면, 이는 curtail(출력제한)된다. 출력제한은 전기를 버리는 것이므로, 수익을 내지 않는다.
시간 인덱스가 $t \in \lbrace 1, 2, …, T \rbrace$ 일 때, 모든 시간의 비용의 합을 최소화하는 계통으로부터의 수전/송전, 에너지저장장치의 충전/방전량을 결정하고자 한다. 최적화 문제는 아래와 같다.
Minimize $ \sum_{t=1}^{T} 0.154 p_{\text{import}}[t] - \sum_{t=1}^{T} 0.065 p_{\text{export}}[t] + \sum_{t=1}^{T} 2 p_{\text{loss}}[t] $
Subject to
$ p_{\text{load}}[t] = p_{\text{pv}}[t] + p_{\text{import}}[t] - p_{\text{export}}[t] + p_{\text{disch}}[t] - p_{ch}[t] + p_{\text{loss}}[t] - p_{\text{curtail}}[t] \quad \forall t$
$ e_{\text{batt}}[t] = e_{\text{batt}}[t-1] + 0.8 p_{\text{ch}}[t] - p_{\text{disch}}/0.8 \quad \forall t,\,\, e_{\text{batt}}[0]=0 $
$ p_{\text{import}}[t] \leq 1.1, \,\, p_{\text{export}}[t] \leq 1.1 \quad \forall t$
위에서 load는 부하, pv는 태양광, import는 계통으로부터의 수전, export는 계통으로의 송전, disch는 배터리 방전, ch는 배터리 충전, loss는 전력 부족 시 loss of load, curtail은 전력 초과 시 출력제한, batt는 배터리이다. $p$는 전력, $e$는 저장된 에너지, $\mu$는 효율이다. $p_{\text{load}}[t]$와 $p_{\text{pv}}[t]$는 input data로써 주어져 있고, 나머지 nonnegative 변수들의 값을 결정한다.
(참고로 보통은 battery의 c-rate까지 고려해야 하지만, Vincent의 논문에서는 배터리가 순간적인 발전량 전부를 유입시킬 수 있다고 가정했으므로 c-rate는 고려하지 않았다.)
위 선형계획 문제를 Python에서 cvxopt 패키지와 glpk solver로 구성하고 푸는 코드는 아래와 같다. (GitHub Repo 링크)
from cvxopt import matrix, spmatrix, sparse, glpk
import numpy as np
import time
load_peak = 2
pv_peak = 12
eff_h2 = 0.65 # 수소-전기 변환효율
capa_batt = 15 # 배터리 용량 (겉보기용량이 아닌, SOC 상하한 고려한 실용량이라 가정)
eff_batt = 0.9 # 배터리 충방전 효율
initialenergy_batt = 0.0
price_h2 = 0.1 # 수소에너지의 가격 (Euro/kWh)
cost_loss = 2 # loss of load penalty (Euro/kWh)
maxrate_h2 = 1.1 # 계통으로부터의 송전/ 계통으로의 수전 의 상한 (kW)
data_load = np.loadtxt("load_test.txt")
data_pv = np.loadtxt("pv_test.txt")
p_load = data_load[24:] * load_peak
p_pv = data_pv[24:] * pv_peak
t=len(p_load)
def block_eye(size):
return spmatrix(1,range(size),range(size))
def block_zeros(row,col):
return sparse(matrix(np.zeros((row,col))))
def block_ones(row,col):
return sparse(matrix(np.ones((row,col))))
def block_batt(size):
return sparse([[block_zeros(size,1)],[block_eye(size)]]) - sparse([[block_eye(size)],[block_zeros(size,1)]])
Aeq_balance = sparse([[-block_eye(t)], [block_eye(t)], [-block_eye(t)], [block_eye(t)], [block_zeros(t,t+1)], [block_eye(t)], [-block_eye(t)]]) # 변수 순서: 송전, 수전, 충전, 방전, 배터리내에너지, loss of load, curtailment
beq_balance = matrix(p_load-p_pv,tc='d')
Aeq_batterydynamic = sparse([[block_zeros(t,t)],[block_zeros(t,t)],[-eff_batt*block_eye(t)],[block_eye(t)/eff_batt],[block_batt(t)],[block_zeros(t,t)],[block_zeros(t,t)]])
beq_batterydynamic = block_zeros(t,1)
lowerbounds = matrix([[block_zeros(1,t)],[block_zeros(1,t)],[block_zeros(1,t)],[block_zeros(1,t)],[matrix([initialenergy_batt])],[block_zeros(1,t)],[block_zeros(1,t)],[block_zeros(1,t)]])
upperbounds = matrix([[maxrate_h2*block_ones(1,t)],[maxrate_h2*block_ones(1,t)],[np.inf*block_ones(1,t)],[np.inf*block_ones(1,t)],[matrix([initialenergy_batt])],[capa_batt*block_ones(1,t)],[np.inf*block_ones(1,t)],[np.inf*block_ones(1,t)]])
A_lowerbound = -block_eye(7*t+1)
b_lowerbound = -lowerbounds.T
A_upperbound = block_eye(7*t+1)
b_upperbound = upperbounds.T
c = matrix([[price_h2*eff_h2*block_ones(1,t)],[-price_h2/eff_h2*block_ones(1,t)],[block_zeros(1,t)],[block_zeros(1,t)],[block_zeros(1,t+1)],[-cost_loss*block_ones(1,t)],[block_zeros(1,t)]])
Aeq = sparse([Aeq_balance,Aeq_batterydynamic])
beq = matrix([beq_balance,beq_batterydynamic])
A = sparse([A_lowerbound, A_upperbound])
b = matrix([b_lowerbound, b_upperbound])
start_time = time.time()
x=glpk.lp(-c,A,b,Aeq,beq,options={ 'msg_lev': 'GLP_MSG_ON'}) # c는 수익 관점의 벡터임, 그러므로 수익의 최'대'화를 위해 '마이너스' c를 입력
elapsed_time = time.time() - start_time
profit = (c*x[1])[0]
print(profit)
특정 1년의 1월 2일~12월 31일에 대해 최적화 수행 시, 비용은 -50유로, 즉 누적해서 50유로의 수익을 낸다 (이는 다음 포스팅에서부터 소개할 강화학습에 대한 validation case이며, 왜 1월 2일부터인지는 다음 포스팅에서 설명한다).
여기서 $t=1$일 때의 $p_{\text{export}}[1]$와 $p_{\text{import}}[1]$을 결정하는 데 쓰이는 정보는, $p_{\text{pv}}[1], p_{\text{pv}}[2], \cdots, p_{\text{pv}}[T]$ 즉 모든 시간의 태양광 발전량 값들 및 $p_{\text{load}}[1], p_{\text{load}}[2], \cdots, p_{\text{load}}[T]$ 즉 모든 시간의 부하 값들이다. 즉 ‘미래를 정확히 알 때의’ control이다.
그러나 이는 비현실적인 가정이다. 현실 세계에서는 시점 $k$의 $p_{\text{export}}[k]$와 $p_{\text{import}}[k]$를 결정하는 데 실제로 쓰일 수 있는 정보가, 과거의 정보 $p_{\text{pv}}[1], \cdots, p_{\text{pv}}[k-1], p_{\text{load}}[1], \cdots, p_{\text{load}}[k-1]$로 한정된다.
이를 보완하기 위한 방법으로, 시점 $k$ 기준으로 시점 $k+1, k+2, \cdots, k+N$ ($N$은 24~168 즉 하루~일주일 정도의 비교적 짧은 기간) 까지에 대한 ‘작은 문제’를 풀어 해를 얻고, 그 해에서 시점 $k$의 control만 취하는 과정을 반복하는 ‘rolling horizon’ 방법이 있다.
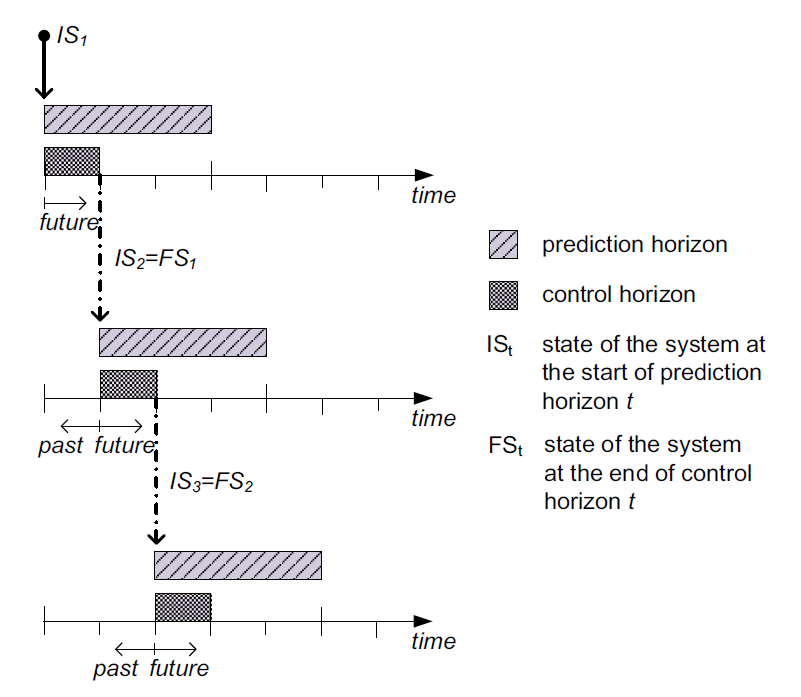 Rolling horizon 기반 control. 가까운 미래에 대한 예측 기반으로 현재의 control을 결정.
Rolling horizon 기반 control. 가까운 미래에 대한 예측 기반으로 현재의 control을 결정.
출처: Silvente et al. (2015)
그러나 이는 두 가지 한계점이 있다.
첫째, 이를 현실에서 사용하려면 단기라도 어쨌거나 미래 $N$시간 동안의 발전량과 부하 ‘예측’이 필요하다는 것이다. 재생발전 비중이 증가할수록 이에 대한 예측이 실제로부터 벗어나기 쉽다는 것은 이미 본문의 맨 위에서 언급했다.
둘째, 해당 control은 현재 및 $N$시간 뒤까지 발생하는 비용의 합만을 최소화하지, 그보다 더 미래까지의 ‘누적비용’은 고려하지 않는다.
강화학습을 쓴다면?
그러면 어떻게 해야 ‘예측 없이 과거 정보만으로’, ‘먼 미래까지의 누적비용을 고려한’ 경제적 control을 도출할 수 있을까?
‘강화학습’ (Reinforcement Learning) 이라는 말을 들어봤을 것이다 (아마 AlphaGo의 학습 원리 등으로).
강화학습은, 주어진 환경에서 특정 상태 (state)에 처했을 때 할 수 있는 행동 (action)들 중 특정 행동을 함으로써 얻는 보상 (reward), 특히 당장의 보상 뿐 아니라 중/장기적 관점에서 미래 보상의 ‘누적 합 (return)’의 기대값을 최대화할 수 있도록, 상태 별 행동을 정하는 규칙 (policy) 을 도출하는 기계학습 방법이다.
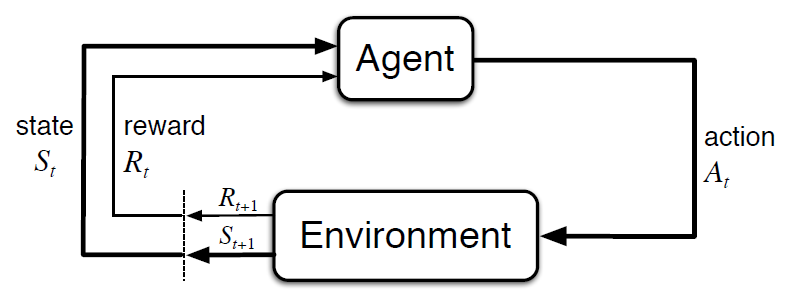 강화학습 개요. State $S_t$에서 Action $A_t$를 취하면 Reward $R_{t+1}$을 얻으면서 State $S_{t+1}$로 전이됨.
강화학습 개요. State $S_t$에서 Action $A_t$를 취하면 Reward $R_{t+1}$을 얻으면서 State $S_{t+1}$로 전이됨.
Vincent의 마이크로그리드 문제에서 state를 특정 N시간 ‘전’까지의 부하와 태양광 발전량, action을 현재 시간에서의 수전/송전으로 두고 강화학습을 적용해 controller를 훈련시키면, 미래 정보 없이도 해당 controller로 ‘경제적인’ 수전/송전 결정을 할 수 있다.
물론 이 controller를 사용할 경우의 누적 비용은, (미래를 다 안다고 가정해서 얻은) 선형계획법 결과 기반 control 시의 비용보다는 클 것이다. 그렇지만 적어도 random control보다는 훨씬 나은 성과를 낼 수 있을 것이다.
실제로 해당 학위논문의 에너지시스템 사례에 대해 수전을 플러스, 송전을 마이너스라 할 때 [-1.1,+1.1] 구간에 대한 uniform distribution을 가정해 all random으로 control을 한다면, validation case에서 누적 비용은 대략 2500~2700유로 정도이다. 그러나 강화학습으로 훈련시킨 controller를 쓰면 27유로로, LP 결과인 -50유로에 상당히 근접한 economic control이 된다.
다음 편부터는 강화학습 개념, 그리고 Vincent의 마이크로그리드 문제에 강화학습을 적용하는 방법 및 결과를 소개한다.
1) 미래를 모를 때의 '경제적' control을 위한 강화학습
2) 강화학습의 기본, Q-learning 리뷰
3) Deep Q-Network를 통한 3-action control 도출
4) DDPG를 이용한 'continuous' control 도출
5) TD3/ SAC 등 '진보된' continuous control을 쓴다면?