지난 포스팅에 이어, 분산에너지시스템 설비의 ‘용량’을 경제성 기반으로 결정하는 문제를 설명한다. 이번에는 지난 포스팅의 내용에 대한 코드, 결과 예시, 그리고 투자회수기간과 전기/ 전기요금/ 탄소 절감량 계산 방법을 설명한다.


1년치 자료로 계산하기

이미 지난 포스팅에서 눈치챈 사람도 있겠지만, 시간별 스케줄 뿐 아니라 용량을 결정하는 문제가 되면서, 문제의 scale이 매우 커졌다.

하루 동안의 배터리 스케줄링 문제에서는 시점의 수가 24개였으나, 수명 20년인 태양광 시스템에 대해 용량을 결정하는 문제에서는 $20 \times 8,760=175,200$개가 되었다. 즉 $p_{\text{grid}}[n,t]$ 항이 175,200개, $p_{\text{ch}}[n,t]$ 항이 175,200개, $p_{\text{disch}}[n,t]$ 항이 175,200개, $e_{\text{batt}}[n,t]$ 항이 175,201개이다. 여기에 $q[n]$ 항 20개, $s_{\text{pv}}$와 $s_{\text{batt}}$도 추가되었다.


이렇게 큰 scale의 문제를 그대로 코드화하려 할 경우, 두 가지 이슈가 생긴다.

첫 번째 이슈는, 계산 시간이 매우 길어진다는 것이다. 필자의 경험 상, 변수가 수십만 개가 되면 Python cvxopt의 경우 계산시간이 수십 분 이상으로 늘어날 수 있고 MATLAB optimization toolbox 등을 써도 분 단위는 걸린다. Input 변수들의 값을 바꿔보면서 계산을 여러 번 돌리는 parametric study를 하고자 할 경우 이는 중요한 이슈다.

두 번째 이슈는, 20년이라는 긴 기간 동안의 `시간별’ 전기부하 데이터와 태양광 발전량 데이터를 구하기 쉽지 않다는 것이다. 기상청 시간별 일사량 및 건물의 스마트미터 계측 모두, 아직은 그만큼 역사가 오래되지 않았기 때문이다. 심지어 일부 기상대에서는 아직도 시간별 일사량 자체를 제공하지 않기도 한다. 이런 경우 없는 데이터를 만들어낸다는 해결책은 마땅치 않은 경우가 대부분이다.


이러한 이슈들 때문에, 많은 연구들에서는 대상 건물의 1년치 시간별 전기부하 자료를 구하고 이 부하가 20년간 똑같이 반복된다고 가정한다. 건물의 전기 사용 추이 및 규모에 큰 변화가 없다고 보는 것이다. 이 경우 태양광 발전량에 대해서도 1년치 시간별 발전량을 구하고 이 발전 패턴이 20년간 똑같이 반복된다고 가정한다.

물론 현실은 그렇지 않지만, 이러한 가정 하의 계산으로도 ‘대략적인’ 최적 용량을 구하는 데 큰 문제는 없다. 어차피 목적함수 계산 시 모든 시간에 대한 총 합을 보는데, 각 시간별로는 오차가 있겠지만 그 오차들을 다 더하면 오차들의 합은 실제와 크게 다르지 않을 것이란 기대가 있기 때문이다. (표본평균의 분산은 표본의 크기가 커질수록 작아지듯)

1년치 자료만을 사용한다면, 각 변수 뒤에 붙던 $[n,t]$는 $[t]$로 바꿀 수 있다. 그리고 변수의 수는 $p_{\text{grid}}[n,t]$ 항이 8,760개, $p_{\text{ch}}[n,t]$ 항이 8,760개, $p_{\text{disch}}[n,t]$ 항이 8,760개, $e_{\text{batt}}[n,t]$ 항이 8,761개, 기본요금 계산을 위해 도입한 $q$, 용량 변수 $s_{\text{pv}}$와 $s_{\text{batt}}$로, 총 35,044개이다.

또한 각 시간별 전기 사용량 요금 $c_{\text{grid}}[t] p_{\text{grid}}[t]$, 기본요금 $12 c_{\text{grid}}^{\text{demand}} q$, 연간 설비 유지보수비용 $ c_{\text{pv}}^{\text{mtn}} s_{\text{pv}} + c_{\text{batt}}^{\text{mtn}} s_{\text{batt}} $ 앞에, factor $\sum_{n=1}^{20} (1+r)^{-n} $을 곱해줘야 한다. 그래야 ‘현재가치로 환산된’ 20년 간의 누적비용이 계산된다.

그리고 현실성을 위해, 추가 제약조건 $e_{\text{batt}}[0] = e_{\text{batt}}[8760]$을 부여해야 한다. 이는 1년치 자료만을 사용하는 최적화 문제가 ‘같은 1년의 반복’을 가정함에 착안해, 해당 1년의 시작 직전 시간의 배터리 내 에너지 저장량과 끝 시간의 배터리 내 에너지 저장량을 동일하게 만든다. 2년차에서 0번째 시간은 1년차의 8760번째 시간과 같기 때문이다.


코드

지금까지의 내용을 반영해, 1년치 자료를 입력으로 받아서 태양광과 배터리 용량을 결정하는 최적화 문제를 구성하고 풀어내는 Python 코드는 아래와 같다. (GitHub Repo 링크)

# -*- coding: utf-8 -*-

from cvxopt import matrix, spmatrix, sparse, glpk
import numpy as np
import matplotlib.pyplot as plt

p_load = np.loadtxt("load_hourly.txt")
p_pv = np.loadtxt("pv_hourly.txt") # 1kW 패널의 시간별 발전량
eleccost = np.loadtxt("eleccost_hourly.txt") # 시간별 kWh당 전력량요금 (기후환경요금/ 연료비조정요금/ 부가세/ 전력산업기반기금 반영 전 금액)
eleccost += (9 + 5) # 기후환경요금 9원/kWh, 연료비조정요금 5원/kWh 반영
eleccost_demandcharge = 8320 # kW당 기본요금
taxrate = 1.137

eff_batt = 0.94
c_rate_batt = 0.5
initialenergy_batt = 0

r = 0.05 # 화폐가치 하락 반영을 위한 할인율

initialcost_pv = 1400000 # 태양광 1kW당 초기투자비
initialcost_batt = 600000 # 배터리 1kWh당 초기투자비 (SOC 고려한 실용량 가정)
mtncost_pv = initialcost_pv * 0.02 # 태양광 1kW당 유지보수비 (매년 발생) 
mtncost_batt = initialcost_batt * 0.01 # 배터리 1kWh당 유지보수비 (매년 발생)

t = 8760

def block_eye(size):
    return spmatrix(1,range(size),range(size)) 

def block_zeros(row,col):
    return sparse(matrix(np.zeros((row,col))))

def block_ones(row,col):
    return sparse(matrix(np.ones((row,col))))

def block_batt(size):
    return sparse([[block_zeros(size,1)],[block_eye(size)]]) - sparse([[block_eye(size)],[block_zeros(size,1)]])


Aeq_balance = sparse([ [block_eye(t)], [-block_eye(t)], [block_eye(t)], [block_zeros(t,t+1)], [block_zeros(t,1)], [matrix(p_pv)], [block_zeros(t,1)]  ])
beq_balance = matrix(p_load,tc='d')

Aeq_batteryenergy = sparse([[block_zeros(t,t)],[-eff_batt*block_eye(t)],[1/eff_batt*block_eye(t)],[block_batt(t)], [block_zeros(t,3)]])
beq_batteryenergy = block_zeros(t,1)

Aeq_batteryenergy_lasthour = matrix([[block_zeros(1,t)],[block_zeros(1,t)],[block_zeros(1,t)],[matrix([1])],[block_zeros(1,t-1)],[matrix([-1])],[block_zeros(1,3)]])
beq_batteryenergy_lasthour = matrix([0])

Aeq = sparse([Aeq_balance,Aeq_batteryenergy, Aeq_batteryenergy_lasthour ])
beq = matrix([beq_balance,beq_batteryenergy, beq_batteryenergy_lasthour])


A_maximumstored = sparse([[block_zeros(t,t)],[block_zeros(t,t)],[block_zeros(t,t)],[block_zeros(t,1)],[block_eye(t)],[block_zeros(t,2)],[-block_ones(t,1)]])
b_maximumstored = block_zeros(t,1)

A_maximumcharge = sparse([[block_zeros(t,t)],[block_eye(t)],[block_zeros(t,t)],[block_zeros(t,t+1)],[block_zeros(t,2)],[-c_rate_batt*block_ones(t,1)]])
b_maximumcharge = block_zeros(t,1)

A_maximumdischarge = sparse([[block_zeros(t,t)],[block_zeros(t,t)],[block_eye(t)],[block_zeros(t,t+1)],[block_zeros(t,2)],[-c_rate_batt*block_ones(t,1)]])
b_maximumdischarge = block_zeros(t,1)

A_maximumgrid = sparse([[block_eye(t)],[block_zeros(t,t)],[block_zeros(t,t)],[block_zeros(t,t+1)],[-block_ones(t,1)],[block_zeros(t,2)]])
b_maximumgrid = block_zeros(t,1)

lowerbounds = matrix([[block_zeros(1,t)],[block_zeros(1,t)],[block_zeros(1,t)],[matrix([initialenergy_batt])],[block_zeros(1,t)],[block_zeros(1,3)]])
A_lowerbound = -block_eye(4*t+4)
b_lowerbound = -lowerbounds.T

upperbounds = matrix([[np.inf*block_ones(1,t)],[np.inf*block_ones(1,t)],[np.inf*block_ones(1,t)],[matrix([initialenergy_batt])],[np.inf*block_ones(1,t)],[np.inf*block_ones(1,3)]]) 
A_upperbound = block_eye(4*t+4)
b_upperbound = upperbounds.T

A = sparse([A_maximumstored, A_maximumcharge, A_maximumdischarge, A_maximumgrid, A_lowerbound, A_upperbound])
b = matrix([b_maximumstored, b_maximumcharge, b_maximumdischarge, b_maximumgrid, b_lowerbound, b_upperbound])

npvfactor = (1/(1+r))*(1-(1/(1+r))**20)/(1-(1/(1+r))) # 초항이 (1+r)^{-1}, 마지막항이 (1+r)^{20}인 등비수열의 합
costfun_pv = initialcost_pv + mtncost_pv * npvfactor # 초기투자비 + 매년 유지보수비(npvfactor를 곱해 현가화)
costfun_batt = initialcost_batt * (1 + (1/(1+r))**10) + mtncost_batt * npvfactor # 초기투자비 + 10년 후 재투자비(현가화) + 매년 유지보수비 (현가화)
costfun_elec = taxrate * eleccost.reshape(1,-1) * npvfactor # 전기 사용량 요금 (현가화), taxrate를 곱해 부가가치세/ 전력산업기반기금 반영
costfun_elec_demand = taxrate * eleccost_demandcharge * 12 * npvfactor # 전기 기본요금 (현가화), 매 월별이므로 12 곱함

c = matrix([[matrix(costfun_elec)],[block_zeros(1,t)],[block_zeros(1,t)],[block_zeros(1,t+1)],[matrix([costfun_elec_demand])],[matrix([costfun_pv])],[matrix([costfun_batt])]]) 

x = glpk.lp(c,A,b,Aeq,beq,options={ 'msg_lev': 'GLP_MSG_ON'})
totalcost = (c*x[1])[0]
capa_pv = np.array(x[1][-2])
capa_batt = np.array(x[1][-1])
p_grid = np.array(x[1][0:t])
p_ch = np.array(x[1][(t):(2*t)]) # Python에서는 t+1:2*t+1 이 아님에 주의
p_disch = np.array(x[1][(2*t):(3*t)])

plt.plot(np.arange(1,73).reshape(-1,1),p_load[0:72])
plt.plot(np.arange(1,73).reshape(-1,1),p_grid[0:72]+p_pv[0:72].reshape(-1,1)*capa_pv)
plt.xlim((0,73))
plt.ylim((0,50))
plt.grid(True)

위 코드의 초반부에서 시간별 전기 부하, 시간별 태양광 발전량, 시간별 전기 요금을 텍스트 파일로부터 불러왔다. 코드 내에 1년 (8,760시간) 내 각 시간별로 대응하는 수치들을 다 써 줄 수 없기 때문이다.

이 때 주의할 점은, 공휴일의 최대수요전력 및 사용전력량은 경부하시간대로 계량하고, 공휴일이 아닌 토요일 최대부하시간대의 사용전력량은 중간부하시간대로 계량한다는 것이다. $\texttt{eleccost_hourly.txt}$에 해당 사항이 반영되어 있는지 확인해야 한다. 그렇지 않으면 전기요금 및 전기요금 절감액이 과다계상된다.

또한 태양광 발전량 데이터가 이상하지 않은지 확인하기 위해, ‘이용률’을 계산해 보아야 한다. 태양광 패널의 이용률은, 정격출력에 8,760시간 (1년) 을 곱한 값 대비 1년간 실제로 발전한 전기 에너지의 양의 비율이다.

이 포스팅 기준으로는, 이용률은 $\sum_{t=1}^{8760} p_{\text{pv}}[t]$, 즉 단순히 $\texttt{pv_hourly.txt}$의 수치들의 합이다. 일반적으로 국내에서는 태양광 이용률이 대략 11~16% 범위 내에 있으며, 이 범위를 크게 벗어날 경우 데이터 출처를 다시 확인해 보아야 한다.


최적 용량 도출 결과

필자가 지정한 케이스 (Peak 부하 1MW로 scaling 처리된 건물 전기부하, 태양광 용량 제한 없다고 가정) 에 대해 계산한 결과, 최적 용량은 태양광 383.9kW + 배터리 205.8kWh로 도출되었다. 또한 특정 3일에 대한 전력 공급 패턴은 아래 그림과 같다.

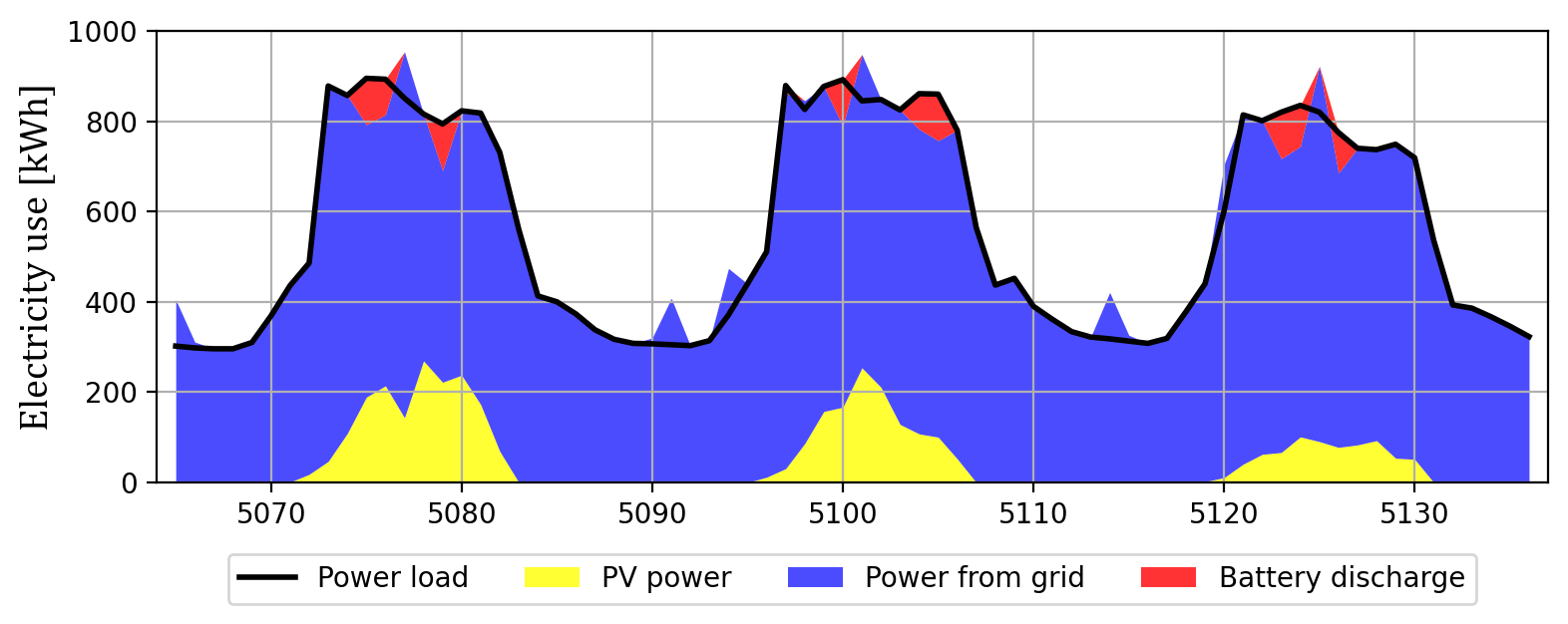result_year 대상 건물에 최적 용량의 태양광과 배터리 설치 시 전력 공급 패턴.

노란 영역은 태양광으로 공급되는 전기에너지, 파란 영역은 수전으로 공급되는 전기에너지, 빨간 영역은 배터리 방전으로 공급되는 에너지이다. 굵은 검정 곡선은 시간별 부하이며, 태양광과 수전의 합이 시간별 부하를 초과한 경우 그 초과분은 배터리로 충전된다.


투자회수기간 및 절감량 계산

위 최적화 문제를 풀었을 때 태양광/ 배터리 용량이 양수인 경우, 시스템 도입 시 ‘현재가치로 환산된 총 비용’이 감소한다는 것은 알 수 있다.

그러나 의사결정권자들의 입장에서는, 태양광/배터리 도입 시 ‘투자회수기간’이 몇 년인지 궁금할 것이다. 설비 투자 결정 주체들은 대개 짧게는 3년에서 길어도 7년 내 투자금 회수를 원한다. 그러나 위 문제의 최적해에서 태양광 용량이 양수더라도, 태양광 투자비가 수명 (20년) 내에는 회수되겠지만 7년 내에 회수되지 않을 수도 있다.

투자회수기간을 계산하려면, ‘태양광/배터리 도입을 통해 절감한 1년간의 전기요금’을 계산해야 한다.

태양광/배터리 도입 ‘전’에는 수전량이 곧 부하와 같다. 그러므로 1년간의 전기 사용량 요금은 $\sum_{t} c_{\text{grid}}[t] p_{\text{load}}[t]$ 이고, 1년간의 전기 기본 요금은 $12 c_{\text{grid}}^{\text{demand}} \text{max}_{t} p_{\text{load}}[t]$ 이다.

태양광/배터리 도입 ‘후’에는, 전기요금이 최적화 문제를 풀어서 구한 $p_{\text{grid}}[t]$와 $q$로 표현되어야 한다. 1년간의 전기 사용량 요금은 $\sum_{t} c_{\text{grid}}[t] p_{\text{grid}}[t]$ 이고, 1년간의 전기 기본 요금은 $12 c_{\text{grid}}^{\text{demand}} q$ 이다. 한편, 태양광/배터리 도입 시 매년 발생하는 설비 유지보수비 $c_{\text{pv}}^{\text{mtn}} s_{\text{pv}} + c_{\text{batt}}^{\text{mtn}} s_{\text{batt}}$ 도 고려해야 한다.

즉, 태양광/배터리 도입을 통한 ‘1년간의’ 전기요금 절감액 $C_{\text{grid}}^{\text{save}}$는 아래 식으로 계산된다.

$C_{\text{grid}}^{\text{save}} = \lbrace \sum_{t} c_{\text{grid}}[t] p_{\text{load}}[t] + 12 c_{\text{grid}}^{\text{demand}} \text{max}_{t} p_{\text{load}}[t] \rbrace - \lbrace \sum_{t} c_{\text{grid}}[t] p_{\text{grid}}[t] + 12 c_{\text{grid}}^{\text{demand}} q \rbrace - \lbrace c_{\text{pv}}^{\text{mtn}} s_{\text{pv}} + c_{\text{batt}}^{\text{mtn}} s_{\text{batt}} \rbrace$

투자회수기간은 아래 식을 만족하는 가장 작은 자연수 $N$이다.

\begin{align} \sum_{n=1}^{N} \frac{C_{\text{grid}}^{\text{save}}}{(1+r)^{n}} \geq c_{\text{pv}}^{\text{init}} s_{\text{pv}} + c_{\text{batt}}^{\text{init}} s_{\text{batt}} \left( 1 + \frac{1}{(1+r)^{10}} \right) \notag \end{align}

또한, 중앙 전력계통으로부터 받는 전기의 ‘절감량’은 $\sum_{t} p_{\text{load}}[t] - \sum_{t} p_{\text{grid}}[t]$ 로 계산된다.

만약 중앙 전력계통에서 공급되는 전기 1kWh 당 탄소배출 계수를 $q_{\text{CO2}}$라 하면, 탄소배출 절감량은 위 절감량에 $q_{\text{CO2}}$를 곱한 값으로 계산된다. 참고로 현재 한국에너지공단의 석유환산톤(toe) 및 배출량 계산기에 따르면, ‘소비’전기에너지에 대한 $q_{\text{CO2}}$는 0.4747tCO2/kWh 이다.


(사족: cvxopt는 무료인 만큼 성능에 한계가 있어 계산 시간이 많이 필요하다. 아마 위 코드 계산도 분 단위로 걸렸을 것이다. ‘유료로’ 수행하는 방법인 MATLAB optimization toolbox 또는 값비싼 상용 solver들 (CPLEX, Gurobi) 을 쓸 경우 당연히 cvxopt보다 훨씬 빠르며, 특히 나중에 설명할 정수 변수가 추가되는 문제에서 속도의 격차가 더욱 커진다.

필자가 (주)블루이코노미전략연구원 (besico) 과 프로젝트를 수행할 때는, besico에서 MATLAB 및 optimization toolbox의 정식 commercial license를 보유하고 있어 이를 사용한다. 발주처 대상으로는, MATLAB 라이선스를 보유하지 않더라도 계산이 가능하도록 MATLAB 코드를 패키지화해 제공하기도 한다.

단 이 시리즈에서는, MATLAB 코드는 설명하지 않을 예정이다. 일종의 영업비밀(!)에 해당하므로.)

선형계획법 기반 분산에너지시스템 최적화

01) 최소비용 시스템과 시간별 자료의 중요성
02) 배터리의 충/방전 스케줄 결정: 수식
03) 배터리의 충/방전 스케줄 결정: Python 코드 및 결과
04) 태양광과 배터리의 '용량' 결정: 목적함수 ('현재가치' 비용) 및 수식
05) 태양광과 배터리의 '용량' 결정: 코드, 결과, 투자회수기간 및 절감량 계산
06) 정수 (integer) 변수 도입으로 현실 설명력 증대
07) 공동주택의 '누진제' 전기요금 (단일계약) 수식
08) 전기 부하와 냉/난방 부하를 동시에 고려 (섹터커플링)
09) '부분'부하 성능 관련 제약들
10) 출력 조정 관련 제약들


(선형계획법 시리즈의 지식들은, 필자가 2012년부터 (주)블루이코노미전략연구원 (대표: 오시덕 박사)과 함께 선형계획법 기반으로 신재생 및 열병합 에너지 시스템 경제성분석/ 최적 에너지시스템 도출 Tool 개발/ 에너지 정책 효과 분석 관련 프로젝트들을 여러 건 수행하며 축적한 ‘기본 지식’에 해당하는 부분임을 밝힌다.)