이번 포스팅에서는, 건물 내 배터리 최적 스케줄 도출 문제를 선형계획법 (Linear Programming) 을 이용해서 풀어본다. Python에서 무료로 쓸 수 있는 cvxopt 패키지의 glpk 모듈로 문제를 풀 것이며, 문제를 코딩하는 방법을 상세히 설명한다.


등호 제약조건 코딩

코딩 시, 각 제약조건들을 개별적으로 입력하는 것이 아니라 등호 제약조건들을 하나의 큰 행렬로 통합해야 하고, 별도로 부등호 제약조건들도 하나의 행렬로 통합해야 한다. (사실 수식으로 입력하면 자동으로 행렬로 변환해주는 프로그램이 있다고 듣기는 했는데, 필자는 이를 써 본 적이 없으며, 지금도 필요성을 느끼지 않는다.)

등호 제약조건들을 통합하는 예시를 보자. 우선 각 시간별 에너지 부하 충족 조건 수식을 다시 쓰면 아래와 같다.

$ p_{\text{grid}}[1] - p_{\text{ch}}[1] + p_{\text{disch}}[1] = p_{\text{load}}[1]$

$ p_{\text{grid}}[2] - p_{\text{ch}}[2] + p_{\text{disch}}[2] = p_{\text{load}}[2]$

$ \vdots $

$ p_{\text{grid}}[24] - p_{\text{ch}}[24] + p_{\text{disch}}[24] = p_{\text{load}}[24]$

각 물리량 별로, 모든 시간의 시간별 값들을 하나로 묶은 열벡터를 정의하자. 일례로

$ \textbf{p}_{\text{load}} = [p_{\text{load}}[1], p_{\text{load}}[2], \cdots, p_{\text{load}}[24]]^{\top} $ 이다.

그러면 24시간 동안의 제약조건을 묶으면 아래와 같은 식이 된다.

$ \textbf{I} \textbf{p}_{\text{grid}} - \textbf{I} \textbf{p}_{\text{ch}} + \textbf{I} \textbf{p}_{\text{disch}} + \textbf{0} \textbf{e}_{\text{batt}} = \textbf{I} \textbf{p}_{\text{load}} $

$\textbf{I}$는 단위행렬이고, $\textbf{0}$는 영행렬이다. 2부에서는 시간별 부하 충족 조건에 $\textbf{e}_{\text{batt}}$를 기재하지 않았지만, 여기서는 기재했음에 주의한다. 그리고 $\textbf{e}_{\text{batt}}$는 25차원 벡터, 그 앞에 붙은 영행렬은 $24 \times 25$ 행렬임에도 주의한다 ($e_{\text{batt}}[t]$는 $t=0,1,\cdots,24$에 대해 정의되므로).

cvxopt에서 등호 제약조건은 $\textbf{A}_{\text{eq}} \textbf{x} = \textbf{b}_{\text{eq}}$ 꼴로 입력되어야 한다, $\textbf{x}$는 우리가 결정해야 할 변수들을 세로로 모두 이어 붙여 만든 열벡터 $[\textbf{p}_{\text{grid}}^{\top},\textbf{p}_{\text{ch}}^{\top},\textbf{p}_{\text{disch}}^{\top},\textbf{e}_{\text{batt}}^{\top}]^{\top}$ 이고 원소 수는 97이다 (수전 24, 충전 24, 방전 24, 배터리내에너지 25). $\textbf{A}$는 그 변수들에 붙는 계수들, $\textbf{b}$는 변수가 아닌 상수들을 의미한다. 그러면, $\textbf{A}_{\text{eq}} \textbf{x} = \textbf{b}_{\text{eq}}$ 꼴의 식은 아래와 같다.

$ \begin{bmatrix} \textbf{I} & -\textbf{I} & \textbf{I} & \textbf{0} \end{bmatrix} \begin{bmatrix} \textbf{p}_{\text{grid}} \newline \textbf{p}_{\text{ch}} \newline \textbf{p}_{\text{disch}} \newline \textbf{e}_{\text{batt}} \end{bmatrix} = \textbf{p}_{\text{load}} $

위 식을 코드로 표현해 보자. 코딩해야 할 것은 $\textbf{A}_{\text{eq}}$와 $\textbf{b}_{\text{eq}}$이다. $\textbf{x}$는 따로 코딩하지는 않는다 (어차피 문제 풀기 전에는 값을 모르니까). 단, 모든 식에서 변수들의 순서는 통일되어야 한다.

$\textbf{A}_{\text{eq}}$에 포함되는 행렬들은 $24 \times 24$ 단위행렬과 $24 \times 25$ 영행렬이다. cvxopt에서는 단위행렬은 $\texttt{spmatrix}$ 모듈로, 그 외 일반적 행렬은 $\texttt{sparse}$ 모듈로 만들 수 있다. 이들을 import 한 후, 아래와 같이 두 함수들 $\texttt{block_eye()}$와 $\texttt{block_zeros()}$를 정의하자.

# -*- coding: utf-8 -*-

from cvxopt import matrix, spmatrix, sparse, glpk
import numpy as np
import matplotlib.pyplot as plt

def block_eye(size): # 단위행렬, 크기는 size x size
    return spmatrix(1,range(size),range(size)) 

def block_zeros(row,col): # 영행렬, 크기는 row x col
    return sparse(matrix(np.zeros((row,col))))

그러면 24x24 단위행렬은 $\texttt{block_eye(24)}$ 로, 24x24 영행렬은 $\texttt{block_zeros(24,24)}$ 로 정의할 수 있다.

여기서 sparse란 `희소하다’ 라는 뜻으로, 0이 많은 행렬에 대해서 0을 곱하거나 더하는 연산을 수행하지 않고, 0을 저장하지도 않는 데이터 타입임을 의미한다 (0이 아닌 원소들 각각이 어느 위치에 있는지만을 저장한다).

이러한 sparse 처리를 해야 행렬 변수가 차지하는 메모리 크기도 작아지고 연산도 빨라진다. 특히 변수가 수만 개를 넘어가면 sparse 처리를 하지 않은 경우와 한 경우의 계산 시간 간 차이가 매우 크며, 구형 컴퓨터의 경우 sparse 처리를 하지 않으면 메모리가 꽉 찰 수도 있다. 그러므로 웬만하면 sparse 처리를 하자.

그리고 시간별 부하를 원소로 하는 numpy array를 $\texttt{p_load}$라 하자. 편의상 전기 부하는 모든 시간에 대해 300kW라 하자 (실제로는 시간에 따라 다르겠지만). 그러면, 위 제약조건을 변수 $\texttt{Aeq_balance}$와 $\texttt{beq_balance}$로 표현한 최종 코드는 아래와 같다.

p_load = 300*np.ones((24,1))

t = 24

Aeq_balance = sparse([ [block_eye(t)], [-block_eye(t)], [block_eye(t)], [block_zeros(t,t+1)] ]) # 블록들은 왼쪽에서부터 수전, 충전, 방전, 배터리내에너지
beq_balance = matrix(p_load,tc='d') # tc='d'는 double형(실수) 의미

Aeq_balance 안이 $[ \textbf{I} \,\, -\textbf{I} \,\, \textbf{I} \,\, \textbf{0} ]$ 이다. 각 블록 행렬은 계통으로부터의 수전 $\textbf{p}_{\text{grid}}$, 배터리에 충전하는 전력 $\textbf{p}_{\text{ch}}$, 배터리로부터 방전되는 전력 $\textbf{p}_{\text{disch}}$, 그리고 배터리 내 저장된 에너지 $\textbf{e}_{\text{batt}}$에 대응한다.

이 때 배터리 내 저장된 에너지에 대응하는 영행렬은 $24 \times 25$ 행렬임에 유의한다 ($24 \times 24$가 아님). 또한 각 블록 행렬을 가로로 이어붙일 때는 각 블록 행렬을 대괄호로 감싸줘야 함에 주의한다. 그리고 $\texttt{beq_balance}$에서 상수 $\texttt{p_pv}$ 를 $\texttt{matrix()}$로 감싸줘야 함에도 주의한다.


이번에는 나머지 등호조건인 배터리 내 에너지 조건을 보자. 해당 조건을 다시 매 시간별 식으로 표현하면 아래와 같다.

$ - 0.9 p_{\text{ch}}[1] + p_{\text{disch}}[1]/ 0.9 - e_{\text{batt}}[0] + e_{\text{batt}}[1]= 0 $

$ - 0.9 p_{\text{ch}}[2] + p_{\text{disch}}[2]/ 0.9 - e_{\text{batt}}[1] + e_{\text{batt}}[2]= 0 $

$\vdots$

$ - 0.9 p_{\text{ch}}[24] + p_{\text{disch}}[24]/ 0.9 - e_{\text{batt}}[23] + e_{\text{batt}}[24]= 0 $

위 식을 보면, $\textbf{p}_{\text{ch}}$와 $\textbf{p}_{\text{disch}}$에 곱해지는 행렬은 단위행렬 꼴이지만, $\textbf{e}_{\text{batt}}$에 곱해지는 행렬은 단위행렬 꼴이 아님을 짐작할 수 있다. 하나의 식에 $\textbf{e}_{\text{batt}}$ 항이 두 개가 나오기 때문이다.

이 제약을 행렬들의 식으로 쓰면, 아래와 같이 된다.

$ \begin{bmatrix} \textbf{0} & -\mu \textbf{I} & \mu^{-1} \textbf{I} \end{bmatrix} \begin{bmatrix} \textbf{p}_{\text{grid}} \newline \textbf{p}_{\text{ch}} \newline \textbf{p}_{\text{disch}} \end{bmatrix} + \begin{bmatrix} -1 & 1 & 0 & 0 & \cdots & 0 & 0 & 0 \newline 0 & -1 & 1 & 0 & \cdots & 0 & 0 & 0 \newline \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \newline 0 & 0 & 0 & 0 & \cdots & -1 & 1 & 0 \newline 0 & 0 & 0 & 0 & \cdots & 0 & -1 & 1 \end{bmatrix} \textbf{e}_{\text{batt}} = \textbf{0} $

$\textbf{e}_{\text{batt}}$의 계수행렬을 함수 $\texttt{block_batt()}$으로 만들고, 위 제약조건을 변수 $\texttt{Aeq_batteryenergy}$와 $\texttt{beq_batteryenergy}$로 구성한 최종 코드는 아래와 같다.

def block_batt(size): # 크기는 size x (size+1)
    return sparse([[block_zeros(size,1)],[block_eye(size)]]) - sparse([[block_eye(size)],[block_zeros(size,1)]])

eff_batt = 0.9 # 충전/방전 효율은 90%로 가정

Aeq_batteryenergy = sparse([[block_zeros(t,t)],[-eff_batt*block_eye(t)],[1/eff_batt*block_eye(t)],[block_batt(t)]])
beq_batteryenergy = block_zeros(t,1)

cvxopt에서는 모든 등호제약조건들의 좌변의 계수들을 결합한 하나의 행렬 $\textbf{A}_{\text{eq}}$와 우변의 상수들을 결합한 하나의 벡터 $\textbf{b}_{\text{eq}}$를 요구한다. 그러므로 두 등호 제약을 결합해서, 최종적으로 하나의 행렬과 하나의 벡터로 만든다.

Aeq = sparse([Aeq_balance,Aeq_batteryenergy]) # ([]) 안의 요소들에 []를 안 붙이면 vstack, []를 붙이면 hstack으로 생각
beq = matrix([beq_balance,beq_batteryenergy])

여기서 $\texttt{Aeq_balance}$와 $\texttt{Aeq_batteryenergy}$는 세로로 이어붙여진다. 이 때는 각 요소를 대괄호로 감싸지 않음에 주의. ($\texttt{beq_balance}$와 $\texttt{beq_batteryenergy}$ 에 대해서도 마찬가지이다)


부등호 제약조건 코딩

다음으로 이 문제의 부등호 제약을 보자. 해당 제약들은 배터리 충전전력/ 방전전력/ 저장에너지의 하한과 상한이다. 그리고 부등호 제약들은 모두 $\textbf{A}\textbf{x} \preceq \textbf{b}$ 꼴로 나타내야 한다 (부등호 방향이 틀리지 않도록 매우 주의해야 한다! 결과가 이상한 경우, 어떤 식에서 부등호 방향을 거꾸로 했기 때문일 경우가 많다).

그러므로 $ p_{\text{ch}}[t]$의 하한과 상한 조건은 아래와 같이 표현하는 것이 좋다.

$ p_{\text{ch}}[t] \leq 50, \,\, -p_{\text{ch}}[t] \leq 0 \quad \forall t$

이는 $ p_{\text{disch}}[t]$, $ e_{\text{batt}}[t]$에 대해서도 마찬가지이다.

단, $ e_{\text{batt}}[0]$의 경우 상한도 0으로 둔다. 또는 $ e_{\text{batt}}[0]$의 초기값을 따로 특정 수 $e_0$로 정한다고 하면, $ e_{\text{batt}}[0]$의 상한과 하한을 모두 $e_0$으로 둔다. 이런 제약조건을 두지 않으면, $ e_{\text{batt}}[0]$이 아무렇게나 정해질 수 있으며 비용 최소화를 위해 배터리의 용량 100 kWh와 같아질 것이다. 그러나 자정에 이미 배터리가 완충되어 있는 상황이 일반적이라고 보기는 어렵다.

각 변수들의 상한을 모은 벡터 $\textbf{u}$에 대한 식은 각 변수들의 계수가 1이고 우변이 상한값들인 부등식 $\textbf{I} \textbf{x} \preceq \textbf{u}$, 하한을 모은 벡터 $\boldsymbol{\ell}$에 대한 식은 각 변수들의 계수가 -1이고 우변이 하한값에 마이너스를 취한 값들인 부등식 $-\textbf{I} \textbf{x} \preceq -\boldsymbol{\ell}$이다.

상한과 하한에 대한 코드는 아래와 같다.

initialenergy_batt = 0
lowerbounds = matrix([[block_zeros(1,t)],[block_zeros(1,t)],[block_zeros(1,t)],[matrix([initialenergy_batt])],[block_zeros(1,t)]]) # 각 변수 별 하한 입력

def block_ones(row,col): # 모든 원소가 1인 행렬 (크기는 row x col)
    return sparse(matrix(np.ones((row,col))))

capacity_batt = 100
c_rate_batt = 0.5
block_onevec = sparse(matrix(np.ones((t,1)))) # t x 1 일벡터 (모든 원소가 1)
upperbounds = matrix([[np.inf*block_ones(1,t)],[c_rate_batt*capacity_batt*block_ones(1,t)],[c_rate_batt*capacity_batt*block_ones(1,t)],[matrix([initialenergy_batt])],[capacity_batt*block_ones(1,t)]]) # 각 변수 별 상한 입력

A_lowerbound = -block_eye(4*t+1) # 부등호 방향 때문에 마이너스 붙음
b_lowerbound = -lowerbounds.T # lowerbounds는 행벡터였음, 이를 열벡터로 바꿈, 부등호 방향 때문에 마이너스 붙음
A_upperbound = block_eye(4*t+1)
b_upperbound = upperbounds.T # upperbounds는 행벡터였음, 이를 열벡터로 바꿈

A = sparse([A_lowerbound, A_upperbound]) 
b = matrix([b_lowerbound, b_upperbound])

이 때 편의를 위해 $\texttt{b_lowerbound}$와 $\texttt{b_upperbound}$에 대응하는 행벡터들 $\texttt{lowerbounds}$와 $\texttt{upperbounds}$를 만들고, 여기에 실제 하한값과 상한값들을 입력하도록 만들었다. 위에서 $\texttt{Aeq}$를 만들 때 각 열이 각 변수에 대응되었으므로, 상한과 하한을 코딩할 때도 각 열을 각 변수로 보는 관점을 그대로 적용할 수 있도록 하였다.

$\texttt{lowerbounds}$의 73번째 원소 (0번째 시간의 배터리 내 에너지)만 주어진 초기값 $\texttt{initialenergy_batt}$이고, 나머지는 전부 0이다.

마찬가지로 $\texttt{upperbounds}$의 73번째 원소 (0번째 시간의 배터리 내 에너지)만 주어진 초기값 $\texttt{initialenergy_batt}$이고, 나머지는 수전 전력에 대해서는 무한대 (즉 따로 상한이 없음), 충전과 방전 전력에 대해서는 배터리 용량에 c-rate를 곱한 값, 1~24번째 시간의 배터리 내 에너지에 대해서는 배터리 용량이다.


목적함수 코딩 및 solver로 풀이

마지막으로, 목적함수를 코딩한다. 목적함수에서 각 변수들에 붙는 계수들을 모은 벡터 $\texttt{c}$를 만든다.

eleccost_offpeak = (87.3+9+5)*1.137 # 경부하 시간의 전력요금 (9와 5는 각각 기후환경요금단가와 연료비조정단가, 1.137은 부가가치세 및 전력산업기반기금 비율)
eleccost_mid = (140.2+9+5)*1.137 # 중간부하 시간의 전력요금
eleccost_peak = (222.3+9+5)*1.137 # 최대부하 시간의 전력요금
eleccost = np.hstack([eleccost_offpeak*np.ones((1,8)),
                      eleccost_mid*np.ones((1,3)),
                      eleccost_peak*np.ones((1,1)),
                      eleccost_mid*np.ones((1,1)),
                      eleccost_peak*np.ones((1,5)),
                      eleccost_mid*np.ones((1,4)),
                      eleccost_offpeak*np.ones((1,2))]) # 24차원 벡터, 각 원소는 해당 시간의 전기요금
c = matrix([[matrix(eleccost)],[block_zeros(1,t)],[block_zeros(1,t)],[block_zeros(1,t+1)]]) # 목적함수에서 변수들의 계수들

여기서 $\texttt{eleccost}$를 $\texttt{matrix()}$로 감싸줘야 함에 주의한다.


이제 선형계획법의 모든 제약조건들과 목적함수에 대응하는 행렬 및 벡터들을 Python 내 변수로 정의했다. 해당 문제를 GLPK 모듈로 풀고, 결과를 확인하는 명령어는 아래와 같다.

x = glpk.lp(c,A,b,Aeq,beq,options={ 'msg_lev': 'GLP_MSG_ON'}) # GLPK solver로 선형계획법 문제를 품
totalcost = (c*x[1])[0] # 24시간 동안의 총 전기요금
p_grid = np.array(x[1][0:24]) # 시간별 수전전기 (Python에서는 배열의 인덱스가 0부터 시작하고, 마지막 인덱스는 포함되지 않음에 주의)
p_charge = np.array(x[1][24:48]) # 시간별 수전전기 중 충전을 위해 배터리로 전달되는 전기 (충전에 따른 손실 발생 전)
p_discharge = np.array(x[1][48:72]) # 시간별 배터리 방전을 통해 부하에 전달되는 전기 (방전에 따른 손실 발생 후)
e_batt = np.array(x[1][72:]) # 시간별 배터리 내 저장된 에너지 (t=0 포함함)


풀이 결과

배터리의 충전/방전 스케줄이 어떤지, 그리고 배터리 내 에너지가 어떻게 변화하는지 그래프로 보자

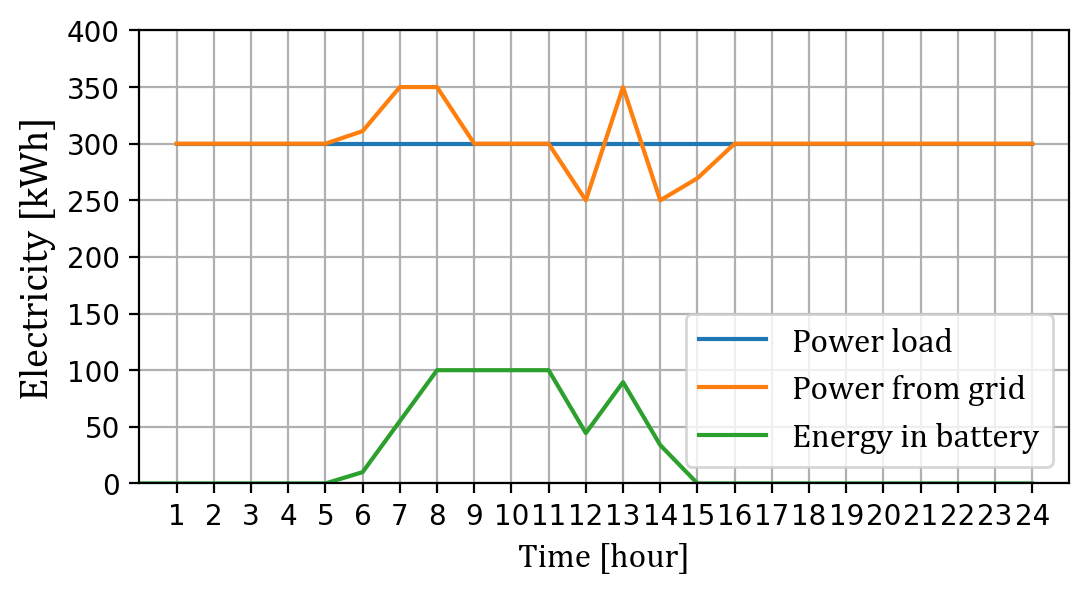result_24hour 24시간 동안의 시스템 operation plot.

경부하 시간대인 5~6시, 6~7시, 7~8시에 수전 (power from grid) 이 부하 (power load) 보다 크며 배터리 내 에너지 (energy from battery) 가 증가한다. 즉 요금이 저렴한 시간에 배터리가 충전된다.

그리고 중간부하 시간대인 8~9시, 9~10시, 10~11시에는 충전도 방전도 되지 않다가, 요금이 가장 비싼 최대부하 시간대인 11~12시에 배터리가 방전되어 수전을 감소시킨다.

그리고 중간부하 시간대인 12~13시에 다시 충전된 후, 다시 최대부하 시간대인 13~14시, 14~15시에 완전히 방전된다. 12~13시에는 경부하가 아닌 중간부하 시간대임에도 불구하고, 바로 뒤에 최대부하 시간대가 오기 때문에 배터리가 충전되었다.

즉 선형계획법으로 구한 충/방전 스케줄은, 예상했던 대로 시간대별 전기요금 차이에 따른 ‘차익거래’를 추구하는 스케줄이다.

선형계획법 기반 분산에너지시스템 최적화

01) 최소비용 시스템과 시간별 자료의 중요성
02) 배터리의 충/방전 스케줄 결정: 수식
03) 배터리의 충/방전 스케줄 결정: Python 코드 및 결과
04) 태양광과 배터리의 '용량' 결정: 목적함수 ('현재가치' 비용) 및 수식
05) 태양광과 배터리의 '용량' 결정: 코드, 결과, 투자회수기간 및 절감량 계산
06) 정수 (integer) 변수 도입으로 현실 설명력 증대
07) 공동주택의 '누진제' 전기요금 (단일계약) 수식
08) 전기 부하와 냉/난방 부하를 동시에 고려 (섹터커플링)
09) '부분'부하 성능 관련 제약들
10) 출력 조정 관련 제약들


(선형계획법 시리즈의 지식들은, 필자가 2012년부터 (주)블루이코노미전략연구원 (대표: 오시덕 박사)과 함께 선형계획법 기반으로 신재생 및 열병합 에너지 시스템 경제성분석/ 최적 에너지시스템 도출 Tool 개발/ 에너지 정책 효과 분석 관련 프로젝트들을 여러 건 수행하며 축적한 ‘기본 지식’에 해당하는 부분임을 밝힌다.)