지난 포스팅에서는 설비의 효율과 COP(성능계수)를 상수로 가정했지만, 실제로는 부하율에 따라 효율과 COP가 달라진다. 이를테면 열병합발전기의 경우, 최대 출력(정격 출력)으로 운전할 때 비해 더 낮은 출력으로 ‘부분부하’운전 시 발전효율이 저하됨이 알려져 있다. 이를 고려하지 않으면 열병합발전기의 경제성을 과대평가하게 될 위험이 있다.

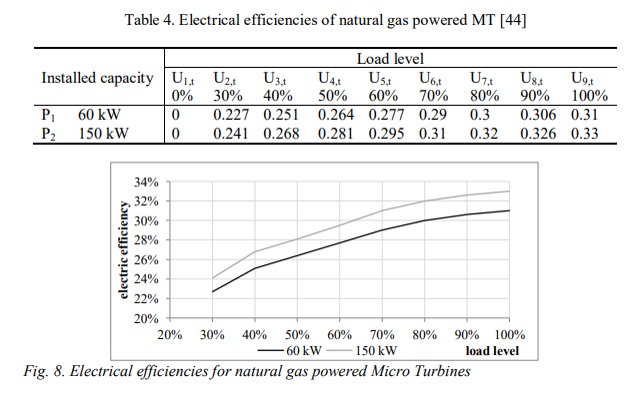chp_eff 열병합발전기의 통상적인 부하율-효율 그래프. 낮은 부하율에서 효율이 저하됨.
출처: “Modeling of non-linear CHP efficiency curves in distributed energy systems”

반대로 냉방기기의 경우, 정격부하 대비 부분부하에서 COP가 더 높다.

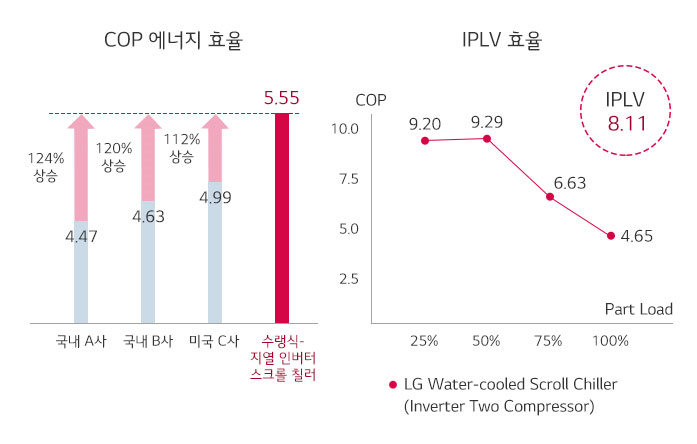cop LG전자의 지열기반 chiller의 부하율별 COP. 일반적인 turbo chiller, 흡수식냉동기도 비슷한 추이를 보임.

이번 포스팅에서는, 선형계획법 문제에서 이러한 ‘부분부하’에서의 효율과 COP를 고려하여 설비의 input-output 관계를 보다 더 현실적으로 모델링하는 수식을 설명한다.


발전기의 부분부하 성능을 고려한 수식

아래 그림은, 정격출력이 100이고 최소부하율이 50%인 가상의 발전기의 연료입력-발전출력 그래프다. 위에서 보인 열병합발전기의 부하율-효율 그래프와는 가로축, 세로축이 다름에 주의한다.

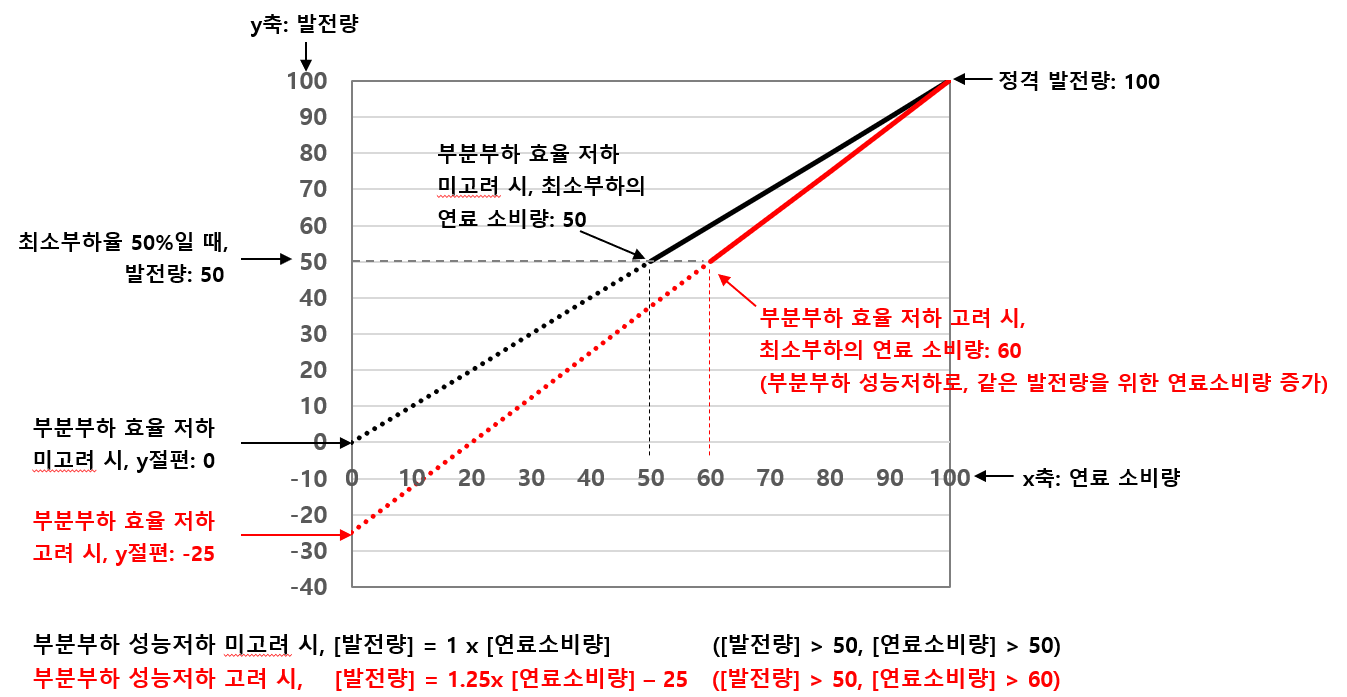chp 연료 입력 - 발전 출력 그래프.

시점 $t$의 연료 소비량을 $f[t]$, 발전량을 $p[t]$라 하자. 위 검정 그래프는 상수 효율 $\eta$을 가정한 경우로, 절편이 없는 직선 $p[t]=\eta f[t]$상의 선분이다.

그러나 부분부하 성능 저하를 고려 시, 위 빨간 그래프처럼, 음의 절편이 있는 직선상의 선분이 된다. 해당 설비의 기동/정지를 나타내는 이진수 $u[t]$를 다시 도입하면 (기동 시 1, 정지 시 0), 위 빨간 그래프는 $p[t] = \eta f[t] + \psi u[t]$로 표현된다 ($\psi$가 절편).

여기서는 연료입력-발전출력 관계를, 최소부하율과 정격출력 두 지점에서의 연료입력-발전출력이 주어질 때 두 점을 잇는 선분으로 근사하였다. $\eta$와 $\psi$를 계산하면 선형계획법을 적용할 수 있다. (해당 ‘선형’ 근사가 실제 발전기 특성에서 크게 벗어나지 않음이 알려져 있다.)

최소부하율이란, 기기 안정성/수명에 해를 끼치지 않는 선에서 최소로 유지할 수 있는 부하율이다. 마치 자전거가 넘어지지 않고 앞으로 나아가려면 최소한의 속도가 필요한 것에 비유할 수 있다.

설비 정격출력을 $S$, 최소부하율을 $\gamma_{min}$라 할 때, 설비의 출력 범위를 표현하는 제약조건은 아래와 같다.

$ u[t] \gamma_{min} s \leq p[t] \leq u[t] s $

$u[t]=0$이면 (즉 정지상태이면) $p[t]=0$이며, $u[t]=1$이면 (즉 기동상태이면) $ \gamma_{min} s \leq p[t] \leq s $ 가 되어 $p[t]$가 최소부하 출력과 정격출력 사이의 값을 가질 수 있다.

여담으로, 위 식에서 $\eta$와 $\psi$는 시간에 따라 다를 수 있다. 이를테면 복합발전 가스터빈의 경우 외기온도가 낮으면 공기밀도 증가로 인해 공급용량이 증가하는 특성이 있어, 외기온도에 따라 시간별로 성능곡선이 다를 수 있다. (물론 이들은 최적화 문제에서 결정되는 변수는 아니고, 외생적으로 결정되는 값이다.)


냉방기기의 부분부하 성능을 고려한 수식

아래 그림은, 정격출력(냉방)이 150kW인 가상의 냉방설비의 전기입력-냉방출력 그래프다. 위에서 보인 chiller의 부하율 별 COP를 적용하였다.

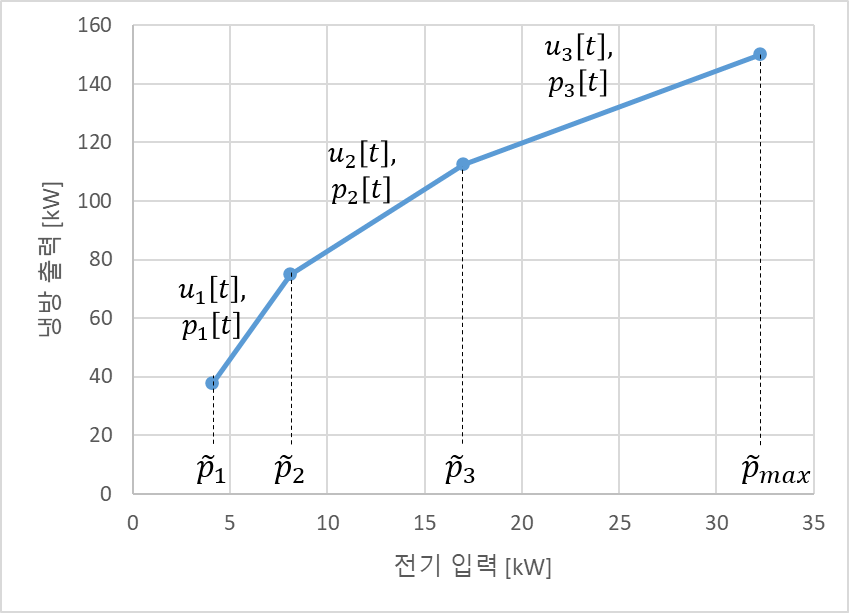chiller 위 LG전자의 지열기반 chiller와 같은 부하율별 COP를 갖는 150kW(냉방출력)급 chiller의 전기 입력 - 냉방 출력 그래프.

냉방기기에 대해서는 보통 부하율 25%, 50%, 75%, 100%에 대한 성능이 주어진다. 즉 4개의 (전기입력,냉방출력) 점이 주어지는데, 4개의 점이 모두 한 선분 위에 있지 않다. 그러므로 더 이상 하나의 선분으로는 표현할 수 없으며, 선형계획을 적용하기 위해서는 3개의 연속된 선분으로 표현되어야 한다.

냉방기기의 (시점 $t$의) 냉방 출력을 $q_{c}[t]$, 전기 입력을 $p_c[t]$라 하자. 그리고 위 그래프의 3개의 선분을 나타내는 일차식들을 각각 $q_c[t]=\alpha_1 + \beta_1 p_c[t]$ (출력기준 부하율 25%~50%), $q_c[t]=\alpha_2 + \beta_2 p_c[t]$ (부하율 50%~75%), $q_c[t]=\alpha_3 + \beta_3 p_c[t]$ (부하율 75%~100%)이라 하자.

그러면 각 시간별로 냉방기기가 가동된다면 위 3개 구간 중 어디에 속하는지 (혹은 가동이 되지 않는지) 여부를 표현하는 이진수 3개의 세트가 있어야 한다. 각각을 $u_1[t]$, $u_2[t]$, $u_3[t]$이라 하자.

또한 전기 입력 변수도 위 3개 구간 각각에 대응하는 3개의 변수 $p_1[t]$, $p_2[t]$, $p_3[t]$으로 두자. 또한 냉방기준 부하율 25%, 50%, 75%, 100%에 대응하는 전기 입력을 각각 $\tilde{p}_1$, $\tilde{p}_2$, $\tilde{p}_3$, $\tilde{p}_{\text{max}}$라 하자. 그러면, 위 그래프는 아래 제약조건들로 표현된다.

$q_c[t] = \alpha_1 u_1[t] + \beta_1 p_1[t] + \alpha_2 u_2[t] + \beta_2 p_2[t] + \alpha_3 u_3[t] + \beta_3 p_3[t] $

$ \tilde{p}_1 u_1[t] \leq p_1[t] \leq \tilde{p}_2 u_1[t] $

$ \tilde{p}_2 u_2[t] \leq p_2[t] \leq \tilde{p}_3 u_2[t] $

$ \tilde{p}_3 u_3[t] \leq p_3[t] \leq \tilde{p}_{\text{max}} u_3[t] $

$ u_1[t] + u_2[t] + u_3[t] \leq 1 $

위 제약을 통해 부분부하 성능 뿐 아니라 기동시의 최소 출력 ($\tilde{p}_1$) 도 반영된다.


‘시간별/ 설비별’ 이진변수에 의한 계산시간 증가 문제

위 방법 사용 시 ‘각 시간별/ 설비별’ 이진변수가 사용되므로 이진변수의 총 갯수가 커진다. 고려 대상 발전기 수가 많아지거나 전체 고려 기간이 길어지면, 풀이에 요구되는 시간이 오래 걸리고 심지어는 사실상 풀리지 않는 문제가 될 수도 있다.

이를테면 1년치 자료를 기반으로 용량을 정하는 문제의 경우 (즉 planning period가 1년, 8760시간), 위 이진변수 기반 제약조건들을 그대로 적용하면 이진변수의 총 갯수가 8,760의 몇 배 이상에 달한다. 이를 그대로 푸는 것은 cvxopt의 glpk 모듈 혹은 MATLAB의 optimization toolbox 정도로는 불가능하며, CPLEX/ Gurobi 등 값비싼 상용 solver로도 꽤나 시간이 걸리는 일이다.


이 경우, 아래와 같은 two-stage 기반으로 문제를 푸는 것이 현실적인 접근법이다.

1st stage: 시간별 이진수가 들어가는 조건식 자체는 추가하되, 이진변수들을 0과 1 사이의 실수로 두고 전체 planning period에 대한 선형계획 문제를 구성해 풀어 설비 별 용량을 구한다. (이를 이진수 조건을 ‘relax’한다고 함.)

2nd stage: 위에서 구한 설비 별 용량을 전제로, 전체 planning period를 여러 개의 짧은 기간들로 나누고 각 기간 (이를테면 하루) 에 대해 위 이진변수 기반 제약조건들을 적용한 최적화 문제를 구성하고 반복적으로 풀어, planning period에 대한 최적 스케줄링을 도출한다.

실제로는 1st stage에서 구한 용량이 전역 최적(global optimum)이 아닐 수 있다. 정확히는 실제 정수선형계획 문제의 최적해 용량 대비 더 낮은 용량일 것이고, 이 경우 global optimum이 아님은 물론, 심지어는 스케줄링 문제가 infeasible problem이 될 수도 있다.

그러므로 선형계획 문제로 도출한 용량을 약간씩 변화시킨 후 다시 2nd stage를 수행해, 더 나은 해가 있는지 탐색해 보는 것이 좋다. 특히 용량이 큰 설비의 대수가 용량변수에 포함되어 있을 경우, 대수를 줄이거나 늘려서 경제성을 원안과 비교해 보는 것이 좋다.

또는 2nd stage에서 각 설비별 ‘추가 용량’ 을 의미하는 slack variable들을 추가하고, 특정 slack variable이 한 번이라도 양수가 되면 1st stage에서 구한 용량에 해당 slack variable을 더한 용량을 전제로 2nd stage를 재수행할 수도 있다.

선형계획법 기반 분산에너지시스템 최적화

01) 최소비용 시스템과 시간별 자료의 중요성
02) 배터리의 충/방전 스케줄 결정: 수식
03) 배터리의 충/방전 스케줄 결정: Python 코드 및 결과
04) 태양광과 배터리의 '용량' 결정: 목적함수 ('현재가치' 비용) 및 수식
05) 태양광과 배터리의 '용량' 결정: 코드, 결과, 투자회수기간 및 절감량 계산
06) 정수 (integer) 변수 도입으로 현실 설명력 증대
07) 공동주택의 '누진제' 전기요금 (단일계약) 수식
08) 전기 부하와 냉/난방 부하를 동시에 고려 (섹터커플링)
09) '부분'부하 성능 관련 제약들
10) 출력 조정 관련 제약들


(선형계획법 시리즈의 지식들은, 필자가 2012년부터 (주)블루이코노미전략연구원 (대표: 오시덕 박사)과 함께 선형계획법 기반으로 신재생 및 열병합 에너지 시스템 경제성분석/ 최적 에너지시스템 도출 Tool 개발/ 에너지 정책 효과 분석 관련 프로젝트들을 여러 건 수행하며 축적한 ‘기본 지식’에 해당하는 부분임을 밝힌다.)