강화학습 기반 마이크로그리드 control - 3) Deep Q-Network를 통한 3-action control 도출
Vincent의 마이크로그리드 사례에서 Q-learning의 concept를 이용하기 위해, 실제로는 수전/송전이 continuous한 값임에도 불구하고, 1.1kW 수전/ 1.1kW 송전/ idle 의 3가지 action만을 고려하기로 했다. 각 action 별 인덱스는 0, 1, 2라 하자.
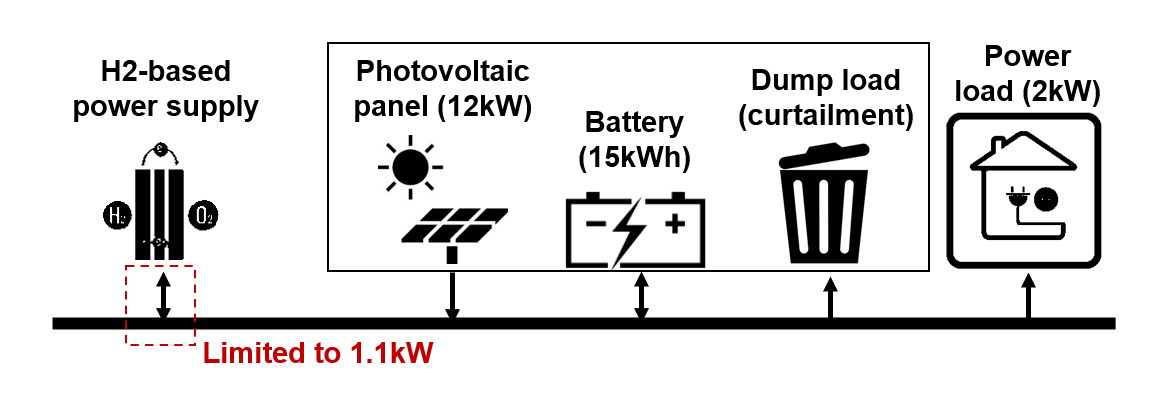Vincent의 연구에서 가정된 마이크로그리드.
이 때 심층신경망은 state를 입력받아 3개 action 각각의 Q-value의 추정치 $Q(s_{t},0), Q(s_{t},1), Q(s_{t},2)$ 를 출력으로 계산한다. 이 심층신경망은 매 훈련 주기마다 튜플 $(s_{t},a_{t},s_{t+1},r_{t+1})$ 의 batch를 받아서 업데이트된다.
심층신경망 구성 및 훈련 컨셉
심층신경망 구성은 아래 그림과 같다.
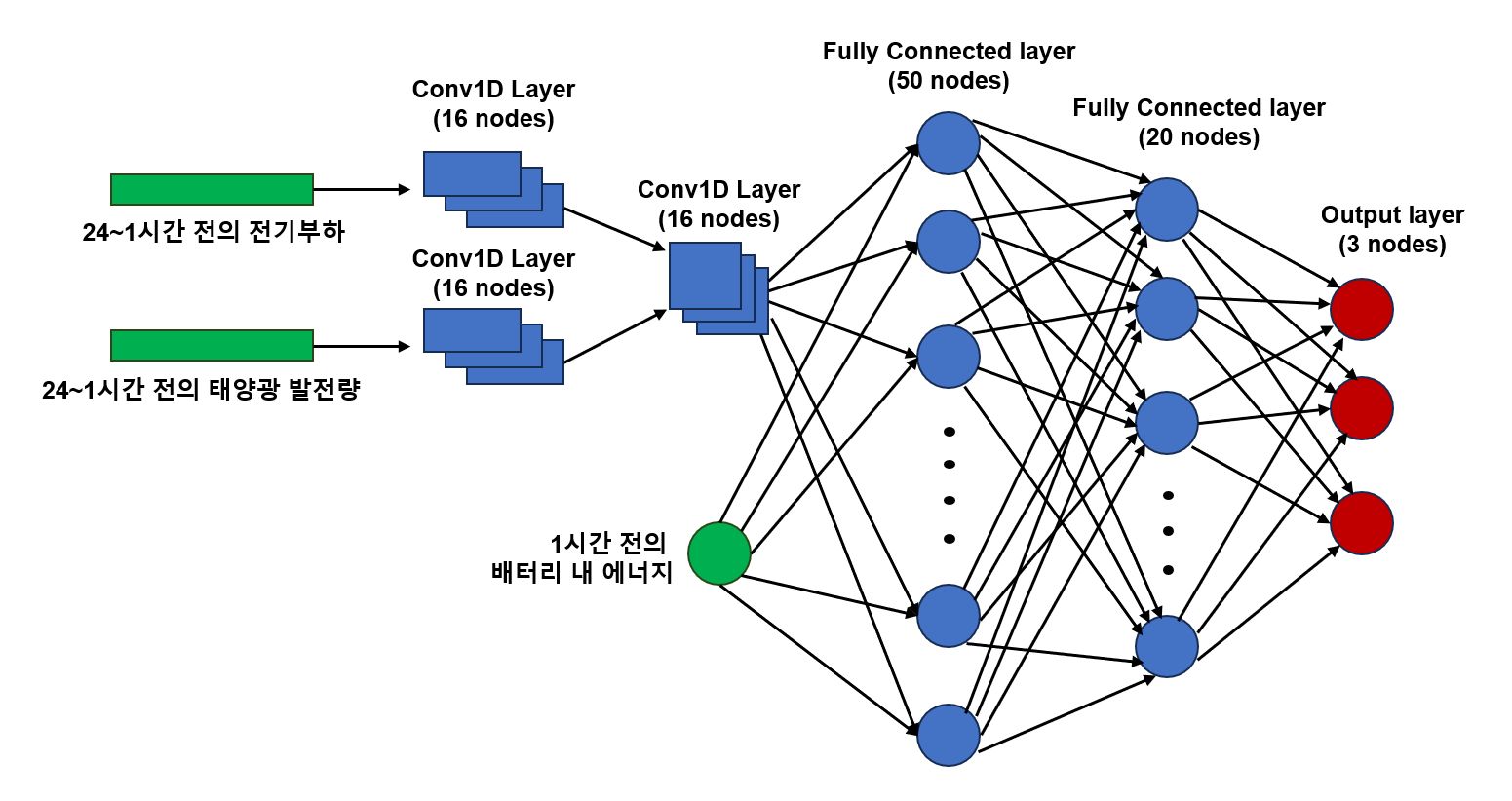Vincent의 연구에서 사용된 심층신경망 구성. (논문의 그림을 필자가 재구성하였음)
직전 24시간의 태양광 발전량은 첫 번째 Conv1D 층에, 직전 24시간의 부하는 두 번째 Conv1D 층에, 그리고 직전 1시간의 배터리 내 에너지양은 위 두 Conv1D층과 연결되는 Dense층에 바로 연결된다.
그리고 Dense층이 하나 더 있고, 이 층을 거쳐서 최종적으로 3개의 output node가 각 action별 Q-value를 출력한다. Conv1D 층을 쓰는 이유는, 태양광 발전량과 부하가 시간적인 정보를 갖고 있으므로 이를 반영하기 위함이다.
해당 심층신경망 훈련을 위한 training set은 특정 2년 (17,520시간) 동안의 시간별 태양광발전량과 부하 자료이다. 해당 모델이 직전 24시간의 정보를 state로 사용하므로 control은 $t=25,26,\cdots, 17520$ 에 대해 정해진다. Validation set은 별도의 특정 1년 (8,760시간) 동안의 시간별 태양광 발전량과 부하 자료이다.
Training set에 대해서는 $\epsilon$-greedy policy를, validation set에 대해서는 greedy policy를 적용해 action을 결정한다.
매 time step (데이터에서의 1시간) 별로 state와 action에 따른 마이크로그리드 내 에너지 흐름 및 수전/송전에 따른 손익 (reward) 와 이번 시점의 배터리 내 에너지 (다음 시점에서의 state임) 를 계산하고, 매 24시간 주기로 심층신경망 훈련을 gradient descent로 수행한다. 이를 training set의 17,520-24 시간에 대해 수행하면 1 epoch이다.
매 심층신경망 훈련 시 사용하는 데이터는 기본적으로 (state, action, reward, next state) 를 묶은 tuple로, 일종의 ‘경험’으로 볼 수 있다. 즉 시점 $t$에서 ($s_{t},a_{t},r_{t+1},s_{t+1}$) 를 추후 훈련에 쓸 수 있도록 buffer에 저장한다.
그리고 24시간 주기의 훈련에서는 직전 24시간의 tuple들이 아닌, buffer 내에서 랜덤하게 뽑은 32개 시간의 tuple들을 이용해 훈련시킨다. 이를 통해 훈련에 쓰이는 tuple들 간의 ‘시간적 상관성’을 감소시켜, 훈련의 효율성을 높일 수 있다.
DQN 코드
이제 훈련 concept는 대략 이해가 될 것이니, 코드를 보자.
이 코드는 필자가 직접 작성하였다. Vincent의 학위논문에서 해당 연구에 사용한 코드의 Github 링크를 제공하나, 각 모듈별로 코드 파일들을 지나치게 분리해 놓아 사용이 여의치 않았다. 이에 필자가 ‘모든 기능들을 한 파일에 넣은 공부용’ 코드를 따로 만들었다. (GitHub Repo 링크)
(코드 작성 시 핸즈온 머신러닝의 강화학습 chapter의 Cartpole 예제에 대한 Deep Q-Network 코드를 참고하였다.)
# -*- coding: utf-8 -*-
import tensorflow as tf
import numpy as np
from tensorflow import keras
import time
### hyperparameters
optimizer = keras.optimizers.Adam(lr=0.005) # learning rate 너무 높으면 발산할 수 있음에 주의
batch_size = 32
discount_factor = 0.98
period_step_fortrain = 24
rewardscalefactor = 1/6
buffer_size = 20000
### microgrid system data
# 시간별 데이터 출처: https://github.com/VinF/deer/tree/master/examples/MG_two_storages/data
PV_prod_train = np.load('BelgiumPV_prod_train.npy') # [0,1] 구간 내로 scaled된 데이터임, unscaling은 play_one_step 함수 내에서 이루어짐
PV_prod_test = np.load('BelgiumPV_prod_test.npy')
load_train = np.load('example_nondeterminist_cons_train.npy') # [0,1] 구간 내로 scaled된 데이터임, unscaling은 play_one_step 함수 내에서 이루어짐
load_test = np.load('example_nondeterminist_cons_test.npy')
prate_h2 = 1.1 # 수전/송전 상한
eff_h2 = 0.65 # 수소-전기 변환효율
capa_batt = 15 # 배터리 용량 (겉보기용량 말고 SOC 상하한 고려한 실용량이라 가정)
eff_batt = 0.9 # 배터리 충방전 효율
initialenergy_batt = 0.0 # epoch의 시작에서 배터리 내 에너지량 (최대저장가능량 대비 상대비율, Qval NN에는 이 상대비율이 입력되며, play_one_step 함수 내에서의 에너지시스템 밸런스 수식에서는 실제 에너지값으로 변환됨
price_h2 = 0.1
cost_loss = 2
load_peak = 2
pv_peak = 12
inputlen_load = 24
inputlen_pv = 24
### Neural net configuration
n_outputs = 3
input_load = keras.layers.Input(shape=(inputlen_load,1)) # 과거 24시간의 부하, shape의 두번째 숫자는 채널 수 (컬러사진의 RGB 등), 채널 수를 정의해야 Conv1D가 작동함
input_pv = keras.layers.Input(shape=(inputlen_pv,1)) # 과거 24시간의 태양광발전량
hidden_conv_load = keras.layers.Conv1D(16, 2, activation='relu')(input_load)
hidden_conv_pv = keras.layers.Conv1D(16, 2, activation='relu')(input_pv)
concat_conv = keras.layers.concatenate([hidden_conv_load,hidden_conv_pv],axis=2)
hidden_conv_concat = keras.layers.Conv1D(16,2,activation='relu')(concat_conv)
flatten_conv = tf.keras.layers.Flatten()(hidden_conv_concat) # Dense층 직전에 Conv층을 Flatten해야 함
input_others = keras.layers.Input(shape=(1)) # 직전 시간의 배터리 내 에너지량
concat_all = keras.layers.concatenate([flatten_conv,input_others])
hidden_dense_1 = keras.layers.Dense(50,activation="relu")(concat_all)
hidden_dense_2 = keras.layers.Dense(20,activation="relu")(hidden_dense_1)
output = keras.layers.Dense(n_outputs)(hidden_dense_2)
model = keras.Model(inputs=[input_load,input_pv,input_others], outputs=[output])
### Policy에 따른 state 별 action 결정 함수
def e_greedy_policy(state,epsilon=0): # epsilon-greedy policy
if np.random.rand() < epsilon: # epsilon의 확률로 exploration
return np.random.randint(3) # action을 랜덤하게 선택
else: # exploitation
input_load = state[0:inputlen_load].reshape(-1,inputlen_load,1) # Conv1D의 input이므로 채널 수 1 명시
input_pv = state[inputlen_load:(inputlen_load+inputlen_pv)].reshape(-1,inputlen_pv,1)
input_others =state[(inputlen_load+inputlen_pv)].reshape(-1,1) # Dense층의 input이므로 채널 수는 필요 없음
Q_values = model((input_load,input_pv,input_others)) # 각 action 별 Q-value 도출
return np.argmax(Q_values[0]) # 가장 큰 Q-value에 대응하는 action 선택
# 주의: for loop 안에서 DNN에 input을 입력해 output 계산 시 model()로 해야지,
# model.predict()로 하면 안 됨! 메모리 누수가 발생함
# (model.predict는 대량의 input data를 'model.predict를 한 번만 호출해서' 처리하는 데 특화됨, https://www.tensorflow.org/api_docs/python/tf/keras/Model#predict 참고)
### replay buffer 정의
from collections import deque
replay_buffer = deque(maxlen=buffer_size)
def sample_experiences(batch_size): # batch_size만큼의 경험들의 state들, action들, reward들, nextstate들의 리스트들을 반환
indices = np.random.randint(len(replay_buffer), size=batch_size) # replay buffer 내 경험들 중 랜덤하게 batch_size만큼의 경험들을 지정 (인덱스 불러옴)
batch = [replay_buffer[index] for index in indices] # 위에서 불러온 인덱스를 이용해 batch_size 만큼의 경험들을 batch 리스트에 담음
states, actions, rewards, next_states = [
np.array([experience[field_index] for experience in batch]) # 하나의 array 안에 batch 내 각 경험별 값들이 들어감
for field_index in range(4)] # 총 4개의 array를 반환, 각각은 (batch 내 sample경험들의) state들, action들, reward들, nextstate들의 리스트임
return states, actions, rewards, next_states
### 1 time step에 대해 action 수행
def play_one_step(profile_load,profile_pv,hour,energy_batt,epsilon,training=False): # 마이크로그리드 시스템의 시간별 operation 모델링
state = np.concatenate( (profile_load[hour-inputlen_load:hour], profile_pv[hour-inputlen_pv:hour], np.array([energy_batt])) )
action = e_greedy_policy(state,epsilon) # epsilon-greedy policy에 따라 action 도출
p_h2_send = 0
p_h2_receive = 0
if action == 0: # 수소로 생산된 전기 수전
p_h2_receive = prate_h2
elif action == 1: # 수소 생산용 전기 송전
p_h2_send = prate_h2
p_load = profile_load[hour]*load_peak # 현재 시간의 부하 (action 결정 기준이 아님!), 입력자료가 [0,1]로 scaled된 걸 unscaling
p_pv = profile_pv[hour]*pv_peak # 현재 시간의 발전량 (action 결정 기준이 아님!), 입력자료가 [0,1]로 scaled된 걸 unscaling
energy_batt = energy_batt*capa_batt # 입력자료가 [0,1]로 scaled된 걸 unscaling
#p_curtail = 0
p_loss = 0
p_net_beforebatt = p_pv - p_load + p_h2_receive - p_h2_send # 태양광 생산, 부하 충족, H2 보내거나 받은 후 수용가 입장에서 전기에너지가 남으면 양수, 부족하면 음수
if p_net_beforebatt >= 0: # 전기에너지가 남으므로 배터리에 저장하고, 만약 배터리도 꽉 찬다면 curtail함
if capa_batt >= energy_batt + p_net_beforebatt*eff_batt: # 배터리에 잔여 충전 가능한 에너지가 위에서 남은 에너지(에서 변환손실 제한 에너지) 이상일 경우
energy_batt_after = energy_batt + p_net_beforebatt*eff_batt
else: # 남은 에너지를 배터리에 다 충전하면 꽉 차고도 남아서, curtail해야 함
energy_batt_after = capa_batt
#p_curtail = (energy_batt + p_net_beforebatt*eff_batt - capa_batt)/eff_batt # 괄호 안은 배터리 내부 기준이며, 수용가 모선 기준 양을 구하려면 eff_batt로 나눠줘야 함
else: # 전기에너지가 부족하므로 배터리 에너지를 써야 함, 배터리 에너지로도 부족하면 loss임
if energy_batt*eff_batt >= -p_net_beforebatt: # 배터리 에너지로 충당 가능한 경우
energy_batt_after = energy_batt + p_net_beforebatt/eff_batt # p_net_beforebatt가 음수이므로 마이너스값이 부족한 에너지'량'이고 그걸 '빼'므로 결과적으로 플러스
else: # 부족해 loss 발생
energy_batt_after = 0
p_loss = -p_net_beforebatt - energy_batt*eff_batt
reward = price_h2*p_h2_send*eff_h2 - price_h2*p_h2_receive/eff_h2 - cost_loss*p_loss
energy_batt_after = energy_batt_after/capa_batt # 배터리 내 저장량을 [0,1] 범위로 scaling함
if training == True:
next_state = np.concatenate( (profile_load[hour-(inputlen_load-1):hour+1], profile_pv[hour-(inputlen_pv-1):hour+1], np.array([energy_batt_after])) )
replay_buffer.append((state, action, reward*rewardscalefactor, next_state)) # replay buffer에는 scaled reward를 넣으며, tuple을 append함에 주의
return energy_batt_after, reward, action # scaled 배터리 내 저장량, unscaled reward, action index 반환
### 심층신경망 가중치 업데이트 수행
def training_step(batch_size):
states, actions, rewards, next_states = sample_experiences(batch_size)
input_load = states[:,0:inputlen_load].reshape(-1,inputlen_load,1)
input_pv = states[:,inputlen_load:(inputlen_load+inputlen_pv)].reshape(-1,inputlen_pv,1)
input_others = states[:,(inputlen_load+inputlen_pv)].reshape(-1,1)
input_load_next = next_states[:,0:inputlen_load].reshape(-1,inputlen_load,1)
input_pv_next = next_states[:,inputlen_load:(inputlen_load+inputlen_pv)].reshape(-1,inputlen_pv,1)
input_others_next = next_states[:,(inputlen_load+inputlen_pv)].reshape(-1,1)
next_Q_values = model((input_load_next,input_pv_next,input_others_next)) # Q-learning을 위해, 'next'state에서의 각 action 별 Q-value 추정치들 반환
max_next_Q_values = np.max(next_Q_values, axis=1) # 각 경험별로 nextstate에 대한 Q-value가 더 높은 행동의 Q-value 사용
target_Q_values = (rewards + discount_factor * max_next_Q_values) # Q-value를 reward와 nextstate에 대한 Q-value(discounted)의 합으로 표현
target_Q_values = target_Q_values.reshape(-1,1) # 뒤의 Q_values와 차원 맞춰줌
mask = tf.one_hot(actions, n_outputs) # 각 경험 별 action을 one-hot encoding 형태로 만들어줌 (각 행이 경험)
with tf.GradientTape() as tape: # 자동 미분
all_Q_values = model((input_load,input_pv,input_others))
Q_values = tf.reduce_sum(all_Q_values * mask, # mask를 곱해서, 각 경험별로 그 state에서 취하지 않은 action에 대해서는 Q-value에 0이 곱해지도록 함
axis=1, keepdims=True) # 각 행 별 합을 구함, 위의 masking 덕분에 그 state에서 취한 action에 대한 Q-value가 됨, keepdims를 True로 설정해 2차원 행렬 형태 유지
loss = tf.reduce_mean(keras.losses.mean_squared_error(target_Q_values,Q_values)) # 평균제곱오차 계산
grads = tape.gradient(loss, model.trainable_variables) # loss 함수를 model의 trainable variables 전체에 대해 미분
optimizer.apply_gradients(zip(grads, model.trainable_variables)) # Adam optimizer로 parameter update 수행, zip으로 gradient와 parameter pair를 맞춰줌
### 훈련 및 검증 수행
profits_test = []
elapsedtime_test = []
count_step_fortrain = 0
max_return_test = -np.inf
for epoch in range(100): # epoch 수 설정
if epoch > 0: # 맨 첫 번째 epoch에서는 훈련을 시작하지 않고 buffer를 채움, 두 번째 epoch부터는 buffer에 sample들이 채워졌으므로 훈련함
start_time = time.time()
### 훈련 (2년치)
hour = 24 # 시작시점
energy_batt = initialenergy_batt # 배터리 내 에너지의 초기값
for step in range(len(load_train)-25): # 데이터 내의 마지막 시점이 nextstate에만 포함될 때까지 (대신 termination state는 따로 없음)
count_step_fortrain += 1
epsilon = max(1 - epoch / 50, 0.1) # epsilon을 1에서 시작해 조금씩 선형적으로 줄임, 이 경우 초반에는 거의 다 exploration이므로 한 epoch가 매우 빨리 계산되나, 중반을 넘어가면 거의 exploitation이며 이 때 매 step마다 DNN을 call하므로 느려짐
energy_batt, reward, action = play_one_step(load_train,PV_prod_train,hour,energy_batt,epsilon,training=True) # energy_batt가 반복 갱신됨
hour += 1 # 다음 시간으로
if epoch > 0 and count_step_fortrain > period_step_fortrain: # 훈련 주기, 매 시간마다 train하면 epoch당 시간이 너무 길어지고 overfitting 우려도 있어, 매 24시간마다 훈련함, 첫 epoch에서는 replay buffer를 채우기만 하고, 나머지 99 epoch 동안 심층신경망 가중치를 업데이트함
training_step(batch_size) # DNN 훈련을 위한 Gradient Descent 수행
count_step_fortrain = 0
### 검증 (1년치)
if epoch > 0:
testcase_actions = []
testcase_battenergy = []
epoch_return_test = 0 # return (각 시점별 수익의 총 합) 초기화
hour = 24 # 시작시점
energy_batt = initialenergy_batt # 배터리 내 에너지의 초기값
for step in range(len(load_test)-24): # 데이터 내의 마지막 시점이 nextstate에만 포함될 때까지 (대신 termination state는 따로 없음)
energy_batt, reward, action = play_one_step(load_test,PV_prod_test,hour,energy_batt,0,training=False) # energy_batt가 반복 갱신됨
testcase_actions.append(action)
testcase_battenergy.append(energy_batt)
epoch_return_test += reward # 누적보상 계산
hour += 1 # 다음 시간으로
profits_test.append(epoch_return_test) # 각 epoch별 총 수익 로그 저장
with open('trajectory_profit_test_dqn.txt', 'w') as f:
for line in profits_test:
f.write(f"{line}\n")
if max_return_test < epoch_return_test: # Validation set에서의 총 수익의 최대값 갱신시마다 저장 (unlearn하게 되더라도 중간에 best performance였던 모델을 남김)
max_return_test = epoch_return_test
model.save_weights('trainedmodel_dqn.h5') # 모델 가중치 저장
with open('trajectory_actions_test_dqn.txt', 'w') as f: # Validation case에서의 시간별 action 로그 저장
for line in testcase_actions:
f.write(f"{line}\n")
with open('trajectory_battenergy_test_dqn.txt', 'w') as f: # Validation case에서의 시간별 배터리 내 저장된 에너지 로그 저장
for line in testcase_battenergy:
f.write(f"{line}\n")
elapsed_time = time.time() - start_time
elapsedtime_test.append(elapsed_time)
print("Validation: profit of epoch {} is {}, maximum profit is {}".format(epoch,round(epoch_return_test,2),round(max_return_test,2)))
print('one epoch 수행에 {}초 걸렸습니다'.format(round(elapsed_time,2)))
with open('trajectory_time_test_dqn.txt', 'w') as f: # 각 epoch별 소요시간 로그 저장
for line in elapsedtime_test:
f.write(f"{line}\n")
Epoch당 계산 시간이 긴데, 이유는 매 시간 별 action을 결정할 때마다 심층신경망에 state를 입력해 Q-value들을 계산하는 과정을, training case에 대해서는 이를 8760x2-24번, validation case에 대해서는 8760-24번을 수행해야 하기 때문이다.
DQN을 통한 discrete control 결과
훈련을 수행하면, validation case 기준으로 불과 몇 epoch만에 누적 비용이 200유로 이하로 줄어든다. 그리고 99 epoch 훈련 동안 validation case에 대해 가장 좋은 결과를 보인 모델의 경우 누적 비용이 27유로이다.
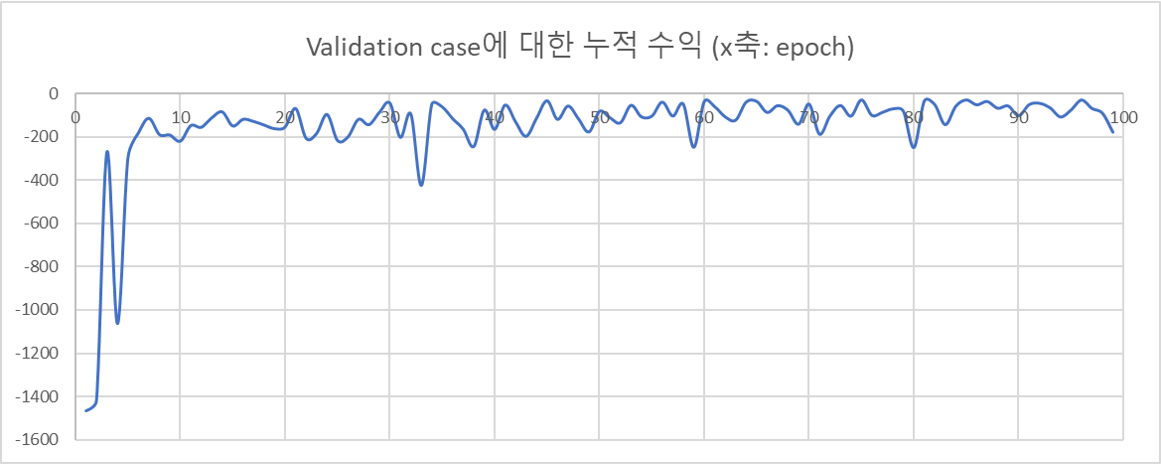훈련 epoch 별 validation case의 누적 ‘수익’.
누적비용 27유로는, 미래를 안다고 가정하고 선형계획법 (Linear Programming, LP) 으로 도출한 control 시의 누적비용 -50유로에 근접한 값이다.
그러므로, 미래를 모르면서 과거 24시간 정보만 갖고 도출한 ‘discrete’ control 것 치고는 훌륭해 보인다. (Random control 시의 누적비용 2500~2700유로와 비교하면 큰 개선이다.)
시간별 action (계통으로부터의 수전) 이 LP와 DQN에서 각각 어떻게 결정되었는지를 아래 그림과 같이 보자.
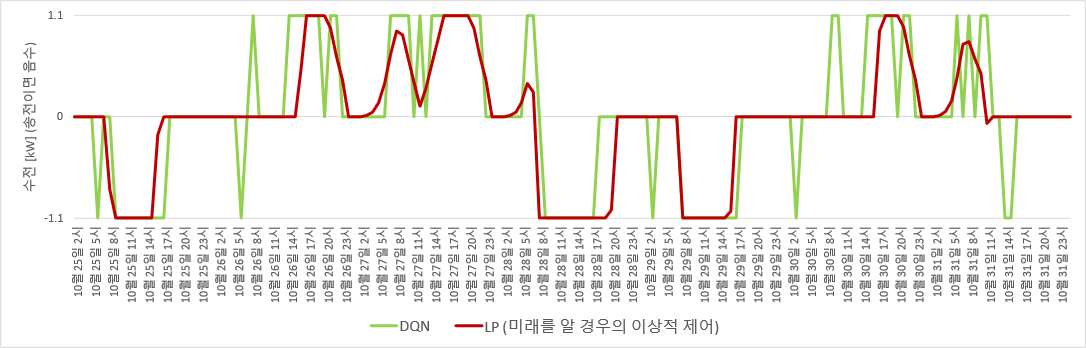DQN으로 도출한 수전/송전 control. LP control과 어느 정도 비슷함.
LP와 DQN으로 도출한 두 control들이 나름 비슷하다. ‘대체로’ LP control에서 수전하는 시간대에 DQN control에서도 수전하고, LP control에서 송전하는 시간대에 DQN control에서도 송전하며, LP control에서 idle인 시간대에 DQN control에서도 idle이다.
특히 LP control은 [-1.1,1.1] 범위 내의 실수로 주어지는 ‘continuous’ control임에도 불구하고, DQN의 action들에 대응하는 최대치 송전/최대치 수전/ idle인 경우가 많다는 점이 특기할 만하다. 이 덕분에, 3-action DQN으로 우수한 economic control을 얻을 수 있는 것으로 보인다.
Continuous control을 한다면?
그렇지만, LP control에서와 DQN control 간에 최대치 송전/ 최대치 수전/ idle 지속시간의 차이가 있고, LP control에서 이 3개 값이 아닌 다른 값인 경우도 (즉 최대치가 아닌 양으로 송전/수전하는 경우도) 분명히 많이 존재한다.
그렇다면 [-1.1,1.1] 범위 내의 실수로 action을 도출하는, continuous control 심층강화학습 기법을 쓰면 어떨까? 최대치가 아닌 송전/ 수전의 가능성까지 반영한 controller를 훈련함으로써, validation case에 대해 더 낮은 누적비용을 달성하는 control 도출이 가능할까?
다음 포스팅에서는, continuous control을 위한 심층강화학습 중 가장 기본적이면서 중요한 방법인 Deep Deterministic Policy Gradient (DDPG) 를 적용하는 방법 및 결과를 설명한다.
1) 미래를 모를 때의 '경제적' control을 위한 강화학습
2) 강화학습의 기본, Q-learning 리뷰
3) Deep Q-Network를 통한 3-action control 도출
4) DDPG를 이용한 'continuous' control 도출
5) TD3/ SAC 등 '진보된' continuous control을 쓴다면?