지난 포스팅에서, Vincent의 태양광 기반 마이크로그리드의 누적 비용을 최소화하는 최적 control 문제를 소개했다. 또한 이를 선형계획법으로 풀 경우 ‘미래의 태양광 발전량과 부하를 안다’라는, ‘비현실적’인 가정 하의 control을 도출함을 보였다.

이번 포스팅에서는 ‘매 시점별로 과거의 자료만을 갖고’ control하는 데 필요한 강화학습의 이론적 내용을 최대한 간단히 소개한다 (강화학습에 대한 상세 내용은 Sutton의 Introduction 참고 바람)


State-action pair 별 누적 보상

먼저, 강화학습에서 가장 널리 쓰이는 방법인인 Q-learning을 간단히 설명한다.

어떤 환경에서 시점 t에 state $s_{t}$에 있고, 이 때 action $a_{t}$를 수행하면 reward $r_{t+1}$을 받으면서 ‘next’ state $s_{t+1}$로 전이된다고 하자.

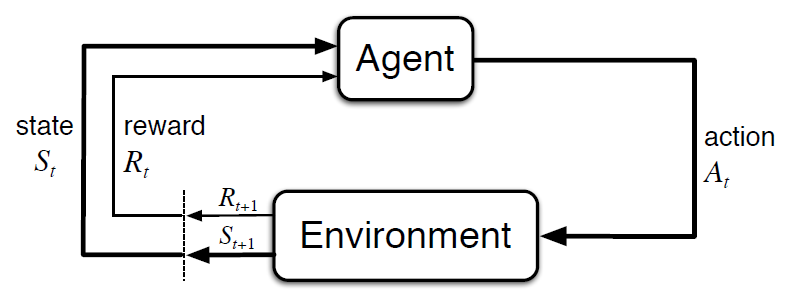reinforcement_basic 강화학습 개요. State $S_t$에서 Action $A_t$를 취하면 Reward $R_{t+1}$을 얻으면서 State $S_{t+1}$로 전이됨.

Vincent의 마이크로그리드 사례에서는, 시점 $t$에서 state는 $t-N, t-(N-1), …, t-1$ 시점들의 태양광발전량과 부하 및 $t-1$시점의 배터리 내 에너지량들의 총 $2N+1$차원 벡터로 두었고, action은 net 수전량 $p_{\text{import}}[t]-p_{\text{export}}[t]$이다 (net 송전 시 마이너스). Reward는 계통으로 송전시의 수익 (양의 reward) 또는 계통으로부터 수전하거나 loss of load가 발생할 때의 비용 (음의 reward) 이다.

참고로 ESS의 충/방전은, 계통 수전/송전 값이 결정되면 에너지 밸런스를 맞추도록 ‘자동으로’ 결정된다고 가정한다. 이런 식으로 action의 자유도 (degree of freedom)를 줄여야 실제 계산이 용이해진다.


각 state $s$에서 action $a$를 할 확률을 나타내는 policy $\pi(a \vert s)$가 주어졌다고 하자. 그리고 시점 $t$에서의 state $s_t$이고, 시점 $t$에서는 poilcy $\pi(a \vert s)$에 관계없이 특정 action $a_t$를 결정하되, 다음 시점인 $t+1$부터는 $\pi(a \vert s)$에 따라 action들 $a_{t+1}, a_{t+2}, \cdots$를 결정한다고 하자.

이 때, state-action pair $(s_t,a_t)$에 대해 ‘미래의 reward들을 합친 누적 보상(return)의 기대값’ $q_{\pi}(s_{t},a_{t})$는 다음과 같다.

$ q_{\pi}(s_{t},a_{t}) = \mathbb{E} [r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \cdots] $

우변에 기대값 기호 $ \mathbb{E}$가 붙은 이유는, 일반적으로는 같은 $s_{t}$에서 같은 $a_{t}$를 수행하더라도, 그 결과인 $r_{t+1}$과 $s_{t+1}$는 그때그때 다를 수 있으며 (즉 random, stochastic일 수 있음), 이에 따라 $t+1$시점 이후의 보상과 상태 전이도 달라질 수 있기 때문이다. 마이크로그리드 케이스에서도, 태양광 발전량과 부하는 외생적으로 random하게 결정되며 이에 따라 수전/송전량이 결정되므로, reward도 random하게 결정된다.

기대값 기호를 $t$에 대한 구분 ‘없이’ 쓴다는 것은, state 간 전이 확률이나 보상별 확률 같은 통계적 속성들이 ‘시간에 관계없이 일정’ 하다고 (즉 stationary하다고) 암묵적으로 전제함을 의미한다. 현실이 이 가정에서 크게 벗어나지 않는지를 고려해서 강화학습의 적정성 여부를 판단해야 한다. (마이크로그리드 케이스의 경우 부하 및 태양광 발전 추이에 급격한 변화가 없을 것이므로, 적절할 것으로 보인다)

$\gamma$는 1보다는 작되 1에 가까운 양수로 discount factor이다. 이를 곱하지 않으면, 환경에서의 행동이 특정 시점에 반드시 끝나는 게 아닌 한 누적비용이 무한대가 될 수 있다. 그러므로 discount factor를 곱해줘야 누적비용이 유한한 값으로 보장된다.


누적 보상 추정: Bellman equation과 Q-learning

한편 시점 $t+1$에 대해서도 $q_{\pi}(s_{t+1},a_{t+1})$이 정의되므로, 위 식은 아래와 같이 $q_{\pi}$에 대해 재귀적인(recursive) 식으로 쓸 수 있다.

$ q_{\pi}(s_{t},a_{t}) = \mathbb{E} [r_{t+1} + \gamma q_{\pi}(s_{t+1},a_{t+1}) ] $

특히 주어진 policy가 ‘최적의’ 즉 optimal policy라면, 시점 $t+1$부터의 action들은 미래 누적비용의 기대값을 최대화도록 선택될 것이다. 따라서 ‘optimal policy 조건 하의’ 누적 보상의 기대값 $q_{\ast}$에 대해, $\text{max}$를 포함하는 아래 식이 성립한다.

$ q_{\ast} (s_{t},a_{t}) = \mathbb{E} [r_{t+1} + \gamma \text{max}_{a_{t+1}} q_{\ast} (s_{t+1},a_{t+1}) ] $

이를 Bellman equation이라 한다.


우리는 optimal policy 및 각 state-action pair 별 $q_{\ast}(s,a)$ 값을 모른다. 그러므로 처음에는 특정 policy 및 $q_{\ast}(s,a)$에 대한 추정량 $Q(s,a)$의 초기값으로부터 출발한다. 그리고 해당 policy 및 $Q(s,a)$를 업데이트시켜서, 점차 optimal policy 및 $q_{\ast}(s,a)$에 근접하게 만들어야 한다.

Bellman equation의 식을 보면, 우변에서 next state에 대해 $q_{\ast}$ 값을 최대화하는 action을 선택함이 전제되어 있다. 이에 착안해, 아래와 같은 $Q(s,a)$의 업데이트 방법을 생각할 수 있다.

$ Q(s_{t},a_{t}) \leftarrow (1-\alpha) Q(s_{t},a_{t}) + \alpha [r_{t+1} + \gamma \text{max}_{a_{t+1}} Q(s_{t+1},a_{t+1})] $

즉 시점 $t$에서 state $s_t$일 때 action $a_t$를 수행하여 reward $r_{t+1}$을 얻고 next state $s_{t+1}$로 전이되었다면, $s_{t+1}$에서 가능한 action들 중 추정량 $Q(s_{t+1},a_{t+1})$를 최대화하는 action $a_{t+1}$을 선택한다고 가정하고 $Q(s_{t},a_{t})$를 업데이트한다. (여기서 $\alpha$는 작은 양수로, learning rate이다)

처음에는 모든 state-action pair들에 대해 $Q(s,a)$를 0으로 초기화하고, 시점 $t$에서 action을 결정해서 $t+1$로 넘어갈 때마다 위와 같이 업데이트 한다.

처음에는 모든 $Q$값이 0이므로 각 state $s$ 별로 $Q(s,a)$를 최대화하는 $a$가 무작위이다. 그러나 업데이트를 수행하면서 ‘실제 환경에서 얻은 정보’인 reward $r_{t+1}$ 를 계속 반영하므로, 업데이트를 거듭할수록 $Q(s,a)$가 점차 $ q_{\ast} (s,a)$에 가까워짐이 알려져 있다. 이에 따라, $Q(s,a)$를 최대화하는 $a$가 무엇인지 뚜렷해지므로 policy도 업데이트되는 셈이다.

이러한 업데이트 방법을 Q-learning이라 한다.


Vincent의 마이크로그리드 사례에서는, 실제 수전량은 -1.1에서 +1.1 사이의 실수이지만 (마이너스값은 송전), 문제를 간단히 하기 위해 세 가지의 ‘discrete’ action들로 구성된 action set (1.1kW로 수전, 1.1kW로 송전, 수전도 송전도 하지 않음 (idle)) 을 가정했다.

위 세 가지 action 각각의 각 action의 인덱스를 0,1,2라 하자. 그리고 시점 $t$에서 상태가 $s_t$일 때 3개의 action들 중 0번 action을 $a_t$로써 정해서 reward $r_{t+1}$을 얻은 후 다음 상태 $s_{t+1}$로 전이되었다고 하자.

그러면 현재의 추정량들 $Q(s_t,0)$, $Q(s_{t+1},0)$, $Q(s_{t+1},1)$, $Q(s_{t+1},2)$를 사용해서, 추정량 $Q(s_t,0)$를 업데이트할 수 있다. 이를 시점 $t, t+1, \cdots$ 에 대해 계속 반복한다.


현재의 action 결정: Exploration/ Exploitation

위에서 $q_{\pi}(s_t,a_t)$를 설명할 때, 시점 $t+1$부터는 policy $\pi$를 따라 action들 $a_{t+1}, a_{t+2}, \cdots$를 결정하되, 시점 $t$에서는 $\pi$에 관계없이 action $a_t$를 결정한다고 했다.

그러면, $a_t$는 어떻게 결정해야 하는가?

가장 직관적인 방법은, 시점 $t$의 state가 $s_t$로 주어졌을 때 $Q(s_t,a_t)$를 최대화하는 action으로 결정하는 것이다. 이러한 $a_t$ 결정 규칙을 ‘greedy’ policy라 한다.

그러나 greedy policy는 controller 훈련을 끝낸 후 ‘validation 및 실제 구동 시’에 적용해야지, ‘훈련 중’에 적용하는 것은 적절하지 않다.

학습 초기에 아직 아무 정보도 학습하지 못했는데 단순히 $Q$ 값이 가장 큰 action만을 계속 하는 것은, 마치 평균적 보상이 다른 여러 개의 슬롯머신을 눈 앞에 두고도, 처음에 고른 몇 개의 슬롯머신 중 좋아 보이는 것만 계속 누르는 것과 비슷하다.

누적 보상을 최대화하려면 어떤 슬롯머신이 가장 (평균적으로) 큰 보상을 주는지 확인하는 절차가 먼저 필요하며, 이를 위해 초반에는 여러 슬롯머신들을 돌아가면서 눌러봐야 한다. 강화학습에서는 이를 exploration(탐색)이라 한다.

탐색을 통해 어떤 슬롯머신이 보상을 많이 주는지 감이 잡히면 그때부터 보상을 많이 주는 슬롯머신을 계속 누르면 되며, 이를 exploitation이라 한다. Q-learning에서 greedy policy는 exploitation’만’ 하는 것에 해당한다.

훈련 시에는 (특히 초반에는) exploration을 겸해서 해 줘야 더 좋은 action을 판별할 가능성이 열린다. 그러므로 시점 $t$에서 $a_t$를 결정할 때, 보통 주어진 값 $\epsilon$만큼의 확률로 $a_t$를 $Q(s_t,a_t)$ 값에 상관없이 random하게 결정한다 (exploration). 그리고 $1-\epsilon$의 확률로 $Q(s_t,a_t)$ 값이 최대가 되는 $a_t$를 결정한다 (exploitation).

이렇게 exploration과 exploitation 간 balance를 갖춘 $a_t$ 결정 규칙을 $\epsilon$-greedy policy라 한다. ($\epsilon$는 훈련 내내 고정되어야 하는 것은 아니며, 훈련 초기에는 크게 하고 훈련이 진행될수록 줄여서 적용할 수도 있다.)

(Exploration/ exploitation에 대해 제대로 이해하고 싶으면, Sutton의 책 2장의 ‘Multi-armed Bandits’를 공부하기 바란다)


State-action pair 수가 매우 많은 경우: Q-value 근사를 위한 딥러닝 사용

지금까지 설명한 방법은, state-action pair의 수가 많지 않을 경우 각 state-action pair별 $Q$값들을 담는 table을 만들어 그대로 적용할 수 있다.

이를테면 아래와 같은 공간에서 상하좌우로 한 칸씩 이동 가능한 환경에서 최단거리를 찾는 문제 (Gridworld) 에서는, 격자 수가 한정되어 있으므로 각 격자(state)-이동방향(action) pair 별로 $Q$값들을 따로 계산할 수 있다.

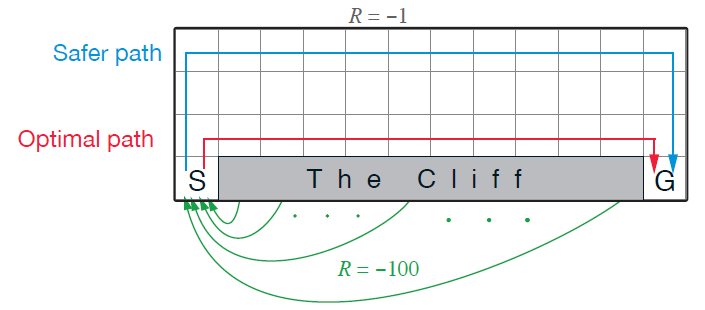gridworld Gridworld 환경. 칸이 38개이고 action은 상하좌우 4개이므로, state-action pair 총 152개 각각에 대해 Q-value를 추정할 수 있다.

하지만 많은 경우 state가 continuous이거나, discrete라도 그 수가 매우 많다.

잘 알려진 cartpole 문제의 경우, action은 ‘수레를 정해진 힘으로 왼쪽으로 가속/ 오른쪽으로 가속’ 딱 두 개의 값 중 하나를 가지는 이진수로 볼 수 있으나, state는 ‘수레의 위치와 속도, 막대의 각도와 각속도’로 4차원의 연속된 벡터로 볼 수 있다. 연속변수이므로, state의 수가 ‘무한대’이다. 그러므로, 각 state-action pair에 대해 table 방식으로 $Q$값들을 따로 계산할 수는 없다.

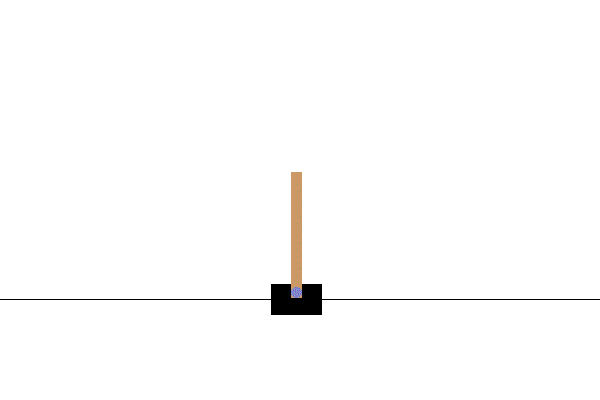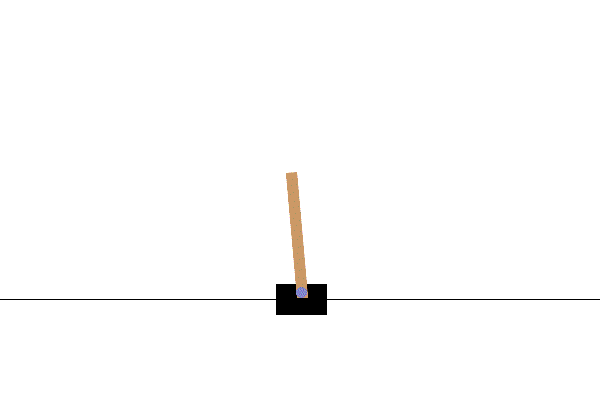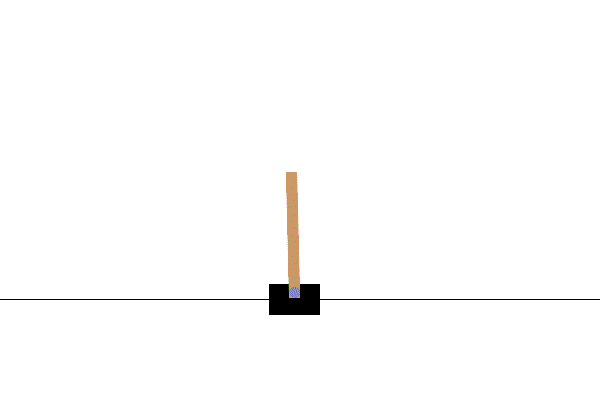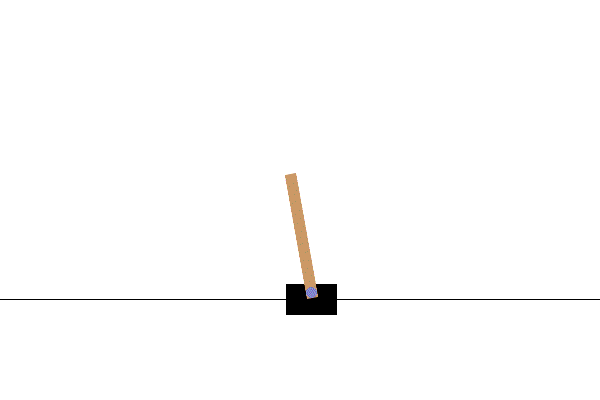cart_pole Cartpole 환경. State 수가 무한하므로, 각 state-action pair에 대한 Q-value를 table 방식으로는 정의할 수 없다.

Vincent의 마이크로그리드 케이스에서도 마찬가지이다. State (직전 $N$시간 동안의 시간별 부하와 태양광 발전량, 그리고 배터리에 저장된 에너지)가 $2N+1$차원의 continuous vector이기 때문이다.

이런 경우 ‘모든 state-action pair 각각에 대해’ $Q$를 계산한다는 것은 사실상 불가능하다. 그렇다면 어떻게 해야 하나?


만약 state-action pair와 Q값 간의 관계가 어떤 domain knowledge에 의해 명확하게 정의될 수 있다면, 해당 관계를 명확한 수식으로 표현하여 $Q$를 쉽게 계산할 수 있을 것이다.

그러나 이 케이스를 포함한 많은 경우, state-action과 $Q$값 간의 관계식을 명확한 수식으로 나타낼 수 있을 것이라 기대되지 않는다.


그렇다면, state $s_t$를 입력으로 받고 각 action 별 $Q(s_t,a_t)$ 값들을 출력으로 하는 심층신경망 (Deep Neural Network, DNN) 모델을 훈련하는 것이 현실적인 방법이다.

심층신경망은 계산비용은 매우 높지만, node 수가 충분하면 어떤 비선형 함수도 근사할 수 있기 때문에 nonlinear function approximator로 기능한다는 점을 이용하는 것이다.

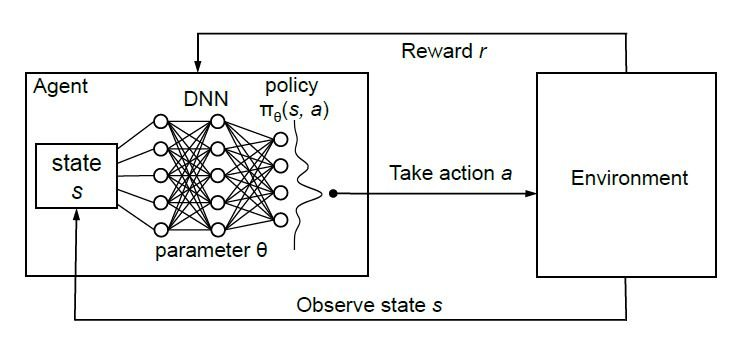reinforcement_deep ‘심층’강화학습 개요. Action 결정이 심층신경망에 기반해 이루어짐.

이 심층신경망 모델은 매 훈련 주기마다 tuple $(s_{t},a_{t},s_{t+1},r_{t+1})$ 의 batch를 받아서 업데이트된다. 이 때 훈련 주기는 1 time step보다 길 수 있으며, batch라 함은 여러 시점들의 tuple들을 한꺼번에 훈련에 사용함을 의미한다.

업데이트 시 최소화 대상 목적함수는 $Q(s_{t},a_{t})$와 $r_{t+1} + \gamma \text{max}_{a_{t+1}} Q(s_{t+1},a_{t+1})$ 간 차이의 평균제곱이다. Gradient descent 기반으로 심층신경망의 가중치를 수정해감에 따라, $Q(s_{t},a_{t})$가 $q_{\ast}(s_{t},a_{t})$에 가까워질 것이라 기대할 수 있다.

이를 Deep Q-Network (DQN) 이라 한다. (위 cartpole 문제도 DQN으로 푼다)


다음 포스팅에서는 마이크로그리드 문제에 Deep Q-Network를 적용하는 과정과 결과에 대해 상세히 설명한다.

강화학습 기반 마이크로그리드 control

1) 미래를 모를 때의 '경제적' control을 위한 강화학습
2) 강화학습의 기본, Q-learning 리뷰
3) Deep Q-Network를 통한 3-action control 도출
4) DDPG를 이용한 'continuous' control 도출
5) TD3/ SAC 등 '진보된' continuous control을 쓴다면?