건축물 별 월별 에너지 사용량 데이터셋 - 2) 월별 사용 추이가 이상한 data point 제거
이전 포스팅에서, 건물 지번별/월별 전기/도시가스 사용량 데이터와 표제부의 결합을 소개했다. 해당 데이터셋을 그대로 쓰면 되는가? 그렇지 않다. 분명히 ‘이상한’ data point들이 존재할 것이며, 이상한 data point들을 ‘전처리’해야 올바른 연구 결과를 얻을 수 있다.
데이터 전처리 종류
가장 먼저 떠올릴 전처리는, 누락이 있는 point 제거이다. 이미 이전 포스팅의 마지막 부분에서 SQLite DB로부터 서울 내 건물들 중 ‘전기 사용량 및 연면적 값의 누락이 없는’ point들만 불러왔다. 여기에 더해, 봄~가을의 도시가스 사용 내역이 있는데 겨울(12, 1, 2월)의 도시가스 사용 내역이 없는 point는 ‘이상한’ point로 보고 제거한다 (상식적으로 도시가스를 쓴다면 겨울에 집중적으로 쓰는 것이 정상이므로).
그 외에 `이상하다’의 기준은, 크게 다음의 두 가지로 볼 수 있다.
1) 12개월 간 월별 에너지 사용량의 추이가 이상함 (전기 사용량 내역을 봤더니 봄/가을 사용량이 여름 사용량보다 월등히 높다든지)
2) 에너지 사용량의 크기(magnitude)가 이상함 (건물은 작은데 비슷한 크기의 타 건물들 대비 에너지 사용량이 지나치게 크다든지)
이러한 ‘이상함’의 이유를 정확히는 알 수 없다. 그러나 이러한 point들은 ‘일반적인’ 건물들에 대한 통계적 에너지 모델링에 도움이 되기는커녕 오히려 해가 될 것이므로, 조치를 취해야 한다.
(필자가 한 가지 발견했던 것은, 지하철 역사의 경우 사용량의 크기가 동일 면적의 타 건물들 대비 매우 컸다는 점이다. 지하철 운전을 위한 전기 사용이 각 역 건물에 대해 계량되는 것으로 추측만 할 뿐이다.)
각 건물의 지번별 데이터는 row의 수가 많다. 서울의 경우 데이터 전처리를 해도 만 단위이다. 데이터가 이 정도로 크면, 회귀분석 등을 할 때 모델을 잘 구성했다는 전제 하에 일관성(consistency)이 있다. 즉, 계수추정량이 실제 값에 가까울 확률이 매우 높다. 그러므로 ‘이상한’ data point는 전부 삭제한다.
이번 포스팅에서는 건물 월별 에너지 사용량의 `추이’가 이상한 data point를 판별하는 방법을 설명한다.
건물 월별 에너지 사용량의 ‘추이’
건물 월별 에너지 사용량의 ‘정상적인’ 추이는 아래 그림과 같다.
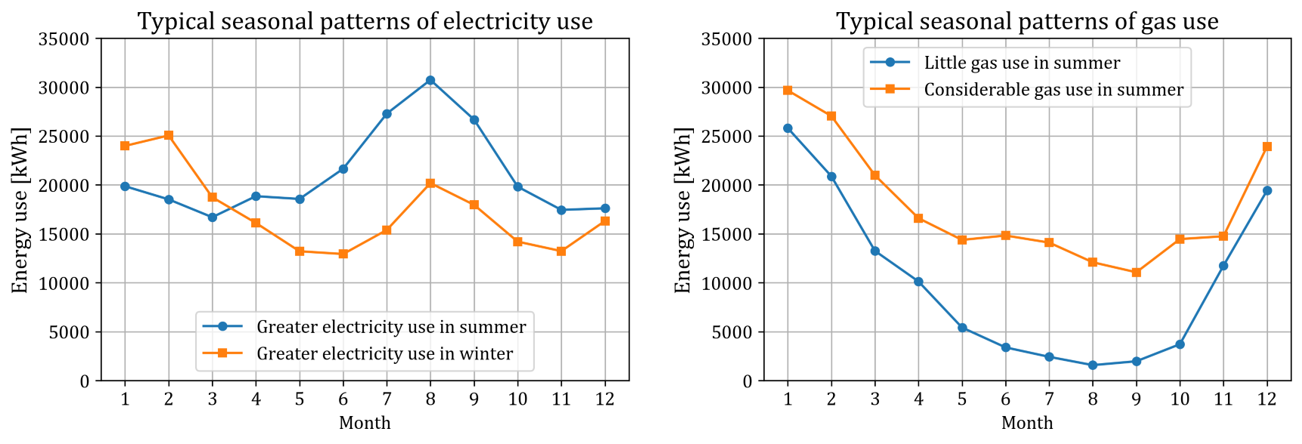일반적인 월별 전기 사용량 추이(좌) 와 가스 사용량 추이(우)
일반적인 월별 전기 사용량 추이의 경우, 냉방으로 인해 여름의 사용량이 상대적으로 크다. 겨울의 전기 사용량은 봄/가을 대비 약간 크지만 전기난방을 하는 경우 건물에 따라 많이 클 수도 있고, 봄/ 가을과 거의 비슷할 수도 있다. 즉 월별 전기 사용량의 추이는 1~12월 plot 기준으로 중간이 튀어나온 압정 모양 혹은 더블유(W)자 모양을 띤다.
일반적인 월별 가스 사용량 추이의 경우, 난방으로 인해 겨울의 사용량이 매우 크다. 여름의 사용량은 대부분은 매우 작으나, 식당/ 목욕탕 등 비중이 큰 일부 건물에서는 여름에도 봄/ 가을과 비슷한 가스 사용량을 보이기도 한다. 즉 월별 가스 사용량의 추이는 유(U)자 모양을 띤다.
그런데, 이와는 매우 다른 추이를 보이는 data point들이 있다. 예를 들면 아래 그림과 같다.
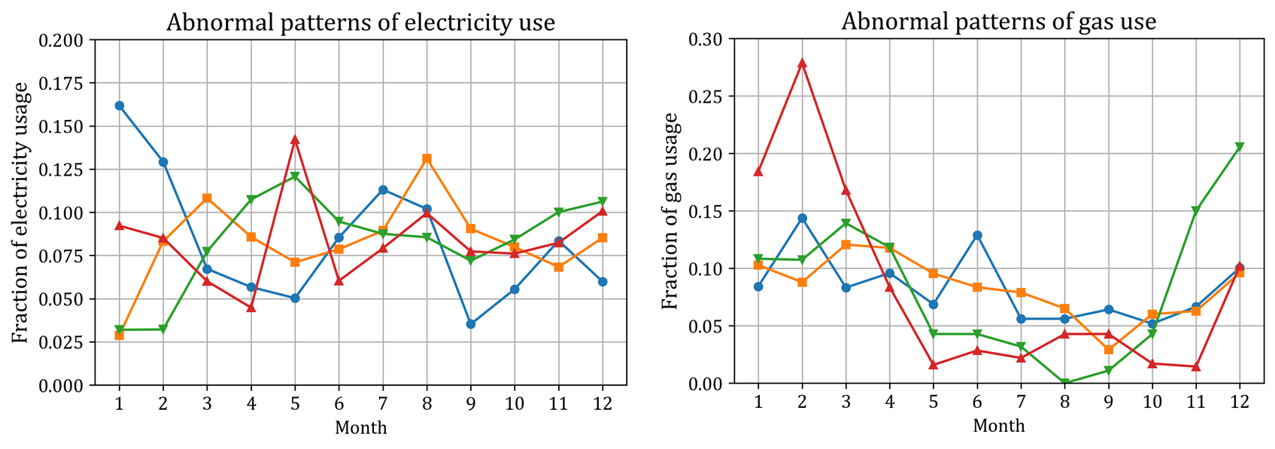비정상적인 월별 전기 사용량 추이(좌) 와 가스 사용량 추이(우)
정확히는, 위 그림은 `각 월별 사용량이 연간 사용량에서 차지하는 비중’을 나타낸 그림이다. 각 월별 전기 사용량을 원소로 하는 12차원 열벡터를 $y_{i}$라 할 때, 위 그림은 $y_{i} / \Vert y_{i} \Vert_{1}$이다. 위 그림에서 보이는 월별 사용량 추이는, 일반적인 추이와 거리가 멀다. 그러므로 해당 data point를 삭제해야 한다.
비정상적인 추이를 보이는 data point 판별 방법
그러면, 이상한 추이를 보이는 data point들은 어떻게 판별할 수 있을까? 월별 비중 그림을 일일이 다 그려서? 데이터 size (data point의 개수) 가 수천개만 되어도 이는 불가능하다. 각 data point 별로 어떤 지표(metric)를 계산 후 그 지표의 크기로 이상한 point를 판별하는 방법이 필요하다.
위에서 언급한 각 월별 사용량 비중을 나타내는 벡터 $y_{i} / \Vert y_{i} \Vert_{1}$를 $\tilde{y}_{i}$라 하자. 그리고 모든 건물들에 대한 $\tilde{y}_{i}$들을 ‘행벡터들을 쌓는 방식으로’ 결합하여 만든 행렬 $\tilde{Y} = [\tilde{y}_{1},\tilde{y}_{2},\cdots, \tilde{y}_{N}]^{\top}$ 을 생각하자.
이 때, $i$번째 data point에 대해 스칼라 값 $\tilde{y}_{i}^{\top} (\tilde{Y}^{\top} \tilde{Y})^{-1} \tilde{y}_{i}$ 를 계산할 수 있다. 이 값이 큰 경우, $\tilde{y}_{i}$는 월별 사용량 비중 벡터들이 만드는 12차원 공간 내에서 다른 data point들로부터 멀리 떨어져 있는 ‘remote’ point임이 알려져 있다.
구체적으로는 $\tilde{y}_{i}^{\top} (\tilde{Y}^{\top} \tilde{Y})^{-1} \tilde{y}_{i}$는 행렬 $\tilde{Y} (\tilde{Y}^{\top} \tilde{Y})^{-1} \tilde{Y}^{\top}$의 대각성분이다. 만약 $\tilde{y}_{i}$가 어떤 회귀모델의 설명변수 벡터인 경우, 이를 hat matrix라고 부른다. Hat matrix의 대각성분은, data point들의 중심으로부터의 표준화된 거리를 의미한다.
(자세한 내용은 Montgomery의 Introduction to Linear Regression의 7단원을 참고하길 바란다.)
그러면 이 스칼라 값이 구체적으로 얼마 이상이면 remote point라고 볼 수 있을까? Rule of thumb가 되는 기준은 $2p/N$으로, $p$는 $\tilde{y}_{i}$가 설명변수 벡터라 할 때 설명변수의 수이고 (월별 에너지 사용량 case의 경우 12), $N$은 data point 수이다.
정리하면, ‘이상한’ 월별 전기 사용량 추이를 갖는 data point들은 아래 과정을 거쳐 판별한다.
1) 모든 data point들에 대한 월별 전기 사용량 자료를 월별 전기 사용량의 ‘비중’ 데이터로 변환 후 각 행이 월별 전기 사용량인 12열짜리 행렬 $\tilde{Y}$로써 결합
2) 위에서 설명한 행렬 $\tilde{Y} (\tilde{Y}^{\top} \tilde{Y})^{-1} \tilde{Y}^{\top}$를 계산
3) $i$번째 대각성분이 $24/N$ 이상인 경우 ‘이상한 월별 전기 사용량 추이’를 갖는 data point로 보고 삭제 이는 월별 가스에 대해서도 마찬가지로 수행한다.
(이상한 추이를 갖는 data point들 그림도, 위 과정을 통해 판별한 것이다)
다음 포스팅에서는 건물 월별 에너지 사용량의 ‘크기(magnitude)’가 이상한 data point를 판별하는 방법을 설명한다.
1) 모든 월에 대한 통합 및 표제부와의 결합 후 SQLite DB화
2) 월별 사용 추이가 이상한 data point 제거
3) 월별 사용량 크기가 이상한 data point 제거
4) 결측치 추정: 조건부 다변량정규분포를 이용해서