이전 포스팅에서는 건물 월별 에너지 사용량의 ‘추이’가 이상한 data point를 판별하는 방법을 설명했다. 이번 포스팅에서는 월별 에너지 사용량의 ‘크기(magnitude)’가 이상한 data point를 판별하는 방법을 설명한다.


에너지 사용량 크기 측면에서의 outlier

상식적으로, 같은 용도의 건물이라면 크기가 큰 건물일수록 에너지 사용량이 큰 경향이 있을 것이다. 이를테면 서울 내 업무용 건물들의 1월 전기 사용량을 연면적 (모든 층의 바닥면적의 합, 단 주차장이나 공용시설 등은 제외) 에 대해 scatter plot하면 아래 그림과 같다.

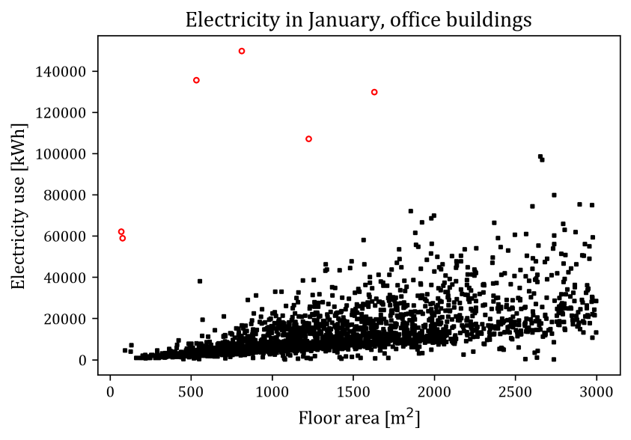outliers x축이 연면적, y축이 1월 전기 사용량. 위쪽에 outlier들이 보임 (붉은 점들).

다소 데이터의 흩어짐(분산)이 크긴 하나, 어쨌든 연면적이 클수록 ‘평균적으로는’ 전기 사용량이 커지는 경향이 있다.


그런데, 위 그림의 붉은 점들은 딱 봐도 ‘크기가 이상한’ data point, 소위 말해서 ‘outlier’이다. 건물 연면적을 고려했을 때 전기 사용량의 값이 지나치게 크다.

이는 측정/기재 오류일 수도 있고, 어쩌면 정말로 저만큼 많은 전기를 쓰는 것일 수도 있다. 그러나 만에 하나 정말로 저렇게 많은 전기를 사용한다고 하더라도, 그런 건물은 일반적이지 않으므로 따로 떼어서 별도의 모델링을 하는 것이 맞다.

즉, ‘일반적인’ 건물들에 대한 통계적 연구 수행을 위해서는 위 outlier들은 제거해야 한다.


Outlier 판별 방법

그럼 outlier는 어떻게 판별하나? 데이터의 size가 그렇게 크지 않고 설명변수가 하나라면, 그냥 그래프를 그려서 눈으로 보고 제거할 수도 있을 것이다. 그러나 데이터 size도 커지고 설명변수도 둘 이상이 되면, 눈으로 보기 매우 힘들다 (이를 테면 반응변수를 에너지 사용량으로 하는 회귀모델에 대해, 설명변수가 건물 연면적 뿐 아니라 건물 층수, 사용연수, 재질 등 여러 가지가 될 수 있다.

그러므로 시각화를 필요로 하지 않으면서 outlier를 판별할 수 있는, 이전 포스팅에서처럼 지표(metric)에 기반해서 판별하는 방법이 필요하다.


여기서 생각해 볼 수 있는 것은, 위 그림에서 outlier들이 있을 때와 없을 때 각 경우에 대해 회귀분석을 했을 때의 직선의 기울기이다. 위 그림 기준으로는 빨간 점들이 없을 때 계산된 직선의 기울기에 비해, 빨간 점들이 있을 때 계산된 직선의 기울기가 더 가파를 것이다. 즉 outlier들이 있을 때 구한 회귀계수와 없을 때 구한 회귀계수 간에 유의미한 차이가 있을 것이다.

반대로, 검정 점들 중 몇 개 정도를 없애고 회귀계수를 계산했다고 하자. 그 결과는 아마, 모든 점들이 있을 때의 회귀계수와 별 차이가 없을 것이다.

그렇다면, 각 data point $i$에 대해, $i$가 포함되어 있을 때 구한 회귀계수와 $i$가 제외될 때 구한 회귀계수 간의 표준화된 차이를 모든 data point들 각각에 대해 구한다면, 그 차이가 큰 data point가 outlier일 것임을 짐작할 수 있다.

이러한 ‘특정 점 $i$의 유무에 따른 회귀계수 간 표준화된 차이’를 Cook’s Distance라 한다. $m$월의 전기 사용량을 반응변수로 하는 회귀모델에 대해, Cook’s Distance의 수식은 아래와 같다.

\begin{align} D_{i}^{elec,m}=\frac{\left({\hat{\beta}}^{elec,m}-{\hat{\beta}}_{-i}^{elec,m}\right)^{\top}X^{\top}X\left({\hat{\beta}}^{elec,m}-{\hat{\beta}}_{-i}^{elec,m}\right)}{k \cdot MSR^{elec,m}} \notag \end{align}

$\hat{\beta}$는 data point $i$를 포함해 모든 data point들이 있을 때 구한 회귀계수이고, $\hat{\beta}_{-i}$는 data point $i$만을 dataset으로부터 뺐을 때 구한 회귀계수이다. $X$는 설명변수 행렬로, $i$번째 행이 $i$번째 data point에 대한 설명변수들로 구성된 행벡터이다 (여기서 설명변수는 연면적, 층수, 사용연도, 재질, …, 그리고 상수항 표현을 위한 1). 분모의 $k$는 설명변수 개수이고, $MSR$은 잔차의 평균제곱합이다.


이 때, 혹자는 계산시간 관련해서 우려를 표할 수 있다. 만약 data point가 수십만 개면, Cook’s Distance들을 계산하기 위해 수십만 번의 회귀분석을 계산해야 되는 것이 아닐까? 그러면 시간이 너무 오래 걸리지 않을까?

다행히도 그렇지 않다. 단 한 번의 회귀분석과 한 번의 행렬 연산으로, 모든 data point 각각에 대한 Cook’s Distance들을 계산할 수 있다. Cook’s Distance의 다른 식은 아래와 같다.

\begin{align} D_{i}^{elec,m}=\frac{\hat{\epsilon}_{i}^{elec,m}h_{ii}}{k \cdot MSR^{elec,m}\left(1-h_{ii}\right)^2} \notag \end{align}

여기서 $\hat{\epsilon}_{i}^{elec,m}$는 $i$번째 잔차, $h_{ii}$는 hat matrix $X\left(X^{\top} X \right)^{-1}X^{\top}$의 $i$번째 대각성분이다.

(역시 자세한 내용은 Montgomery의 Introduction to Linear Regression의 7단원을 참고하길 바란다.)


필자가 알기로는 Cook’s D에는 어떤 rule of thumb로써의 수치가 있지는 않은 듯 하다. 사전에 정의한 갯수만큼의 데이터를, Cook’s D가 큰 순서대로 제거하는 것이 현실적인 방법으로 보인다.

단, 주의할 점은, 한 번의 Cook’s D 계산 후 data point 여러 개를 제거하면 안 된다. Cook’s D가 가장 큰 ‘하나의’ point만 제거하고, 다시 모든 point Cook’s D를 계산해서 또 하나를 제거하고 다시 계산하는 과정을 반복해야 한다.

이는 Cook’s D 자체가 ‘하나의’ data point의 유무 간 차이에 대해 정의되기 때문이다.

만약 어떤 dataset에 대해 Cook’s D를 계산했더니 point $i$에 대해 Cook’s D가 가장 크고 $j$에 대해 Cook’s D가 두 번째로 크다고 하자. 이 때 point $j$에 대한 Cook’s D는, point $i$가 dataset에 있다는 가정 하에 계산된다. 그런데 우리는 outlier를 제거해나가야 하므로, Cook’s D가 가장 큰 outlier $i$가 dataset에 있다는 가정 하에 나머지 point들에 대한 outlier 여부를 판단하는 것은 부자연스럽다.

건축물 별 월별 에너지 사용량 데이터셋

1) 모든 월에 대한 통합 및 표제부와의 결합 후 SQLite DB화
2) 월별 사용 추이가 이상한 data point 제거
3) 월별 사용량 크기가 이상한 data point 제거
4) 결측치 추정: 조건부 다변량정규분포를 이용해서