재생발전 비중이 높은 전력시장에 대한 심화 주제들
필자가 정리했던 Jalal Kazempour 교수의 전력시장 강의에서 reference로써 추천한 책으로, Integrating Renewables in Electricity Markets: Operational Problems 이 있다.
강의 내용에 더해 해당 책을 공부하며, 하루전 시장과 실시간 시장으로 구성된 전력시장의 수리모델링에 대해 더 깊게 이해할 수 있었다.
앞으로 우리나라에서도 2024년부터 제주도에서 실시간 시장이 시범 실시되며 몇 년 내로 육지에서도 실시될 예정인 만큼, 에너지시스템 모델링 전문가를 지향한다면 해당 주제에 대해 미리 공부해놓는 것이 당연하다 하겠다.
이번 포스팅에서는, 해당 책 내용 중 Jalal 교수의 강의에서 다루지 않았으나 현실 세계에서 자주 볼 법한, 그러면서도 지나치게 복잡하지는 않은 (즉 우선순위가 높아 보이는) 모델들을 정리하였다.
예비력을 포함한 market clearing
급전 계획에서 각 발전기의 출력은, 총 공급과 총 수요가 일치하도록 결정된다. 그런데 실제로는, 계획 대비 실시간에서의 총 수요가 더 클 수 있다. 이 때 수요 증가에 ‘신속하게’ 대응할 수 있도록, 예비력 (reserve capacity) 을 확보해야 한다.
예비력을 제공하는 발전기에 대해, 급전과 별개로 예비력에 대해서도 비용을 지불하는 경우에 대한 최적 계획 문제를 보자.
발전기 A는 용량 100 MW, offer price는 MWh당 10달러이고, 발전기 B는 용량 100 MW, offer price는 MWh당 20달러이다.
한편 예상되는 총 수요는 130 MW 이지만, 예비력을 20 MW 확보해야 한다. 발전기 A는 예비력을 무상으로 제공하는 반면, 발전기 B의 예비력에 대한 offer price는 MW당 25달러이다.
이 때 발전량과 예비력을 동시에 구하는 market clearing problem은 아래와 같다. (Unit commitment 제약들은 무시했다.)
Min. $10 P_A + 30 P_B + 0 R_A + 25 R_B$
Subject to
$ P_A + P_B = 130$ : $\lambda_P$
$ R_A + R_B = 20$ : $\lambda_R$
$ P_A + R_A \leq 100$, $P_A \geq 0$, $R_A \geq 0$
$ P_B + R_B \leq 100$, $P_B \geq 0$, $R_B \geq 0$
예상 수요와 요구되는 예비력을 충족해야 하면서, 각 발전기 별로 실제 발전량과 예비력 제공량의 합이 용량을 초과할 수 없다는 제약 하에, 비용을 최소화하는 발전기 별 발전량과 예비력 제공량을 구한다.
이 때 예상 수요 충족 제약의 dual variable $\lambda_P$는 energy price이고, 요구되는 예비력 충족 제약의 dual variable $\lambda_R$은 reserve capacity price이다.
위 문제에서는 예비력 제공량이 미리 정해진 요구치 20 MW 를 반드시 충족해야 했다. 여기에는, 총 수요가 갑자기 20 MW 증가할 가능성이 어느 정도 있으며 해당 수요 증가분을 충족하지 못할 경우 심각한 손해를 입을 것이라는 가정이 암묵적으로 깔려 있다.
만약 수요가 갑자기 20 MW 증가할 가능성이 매우 낮거나, 증가한 수요를 충족하지 못하더라도 그로 인해 입는 손실이 그다지 크지 않다면, 예비력을 20 MW 제공하는 것이 경제성 측면에서 최선이 아닐 수 있다.
이를테면 수요가 갑자기 20 MW 증가할 확률이 5퍼센트이고, 갑자기 증가한 수요를 충족하지 못할 경우의 경제적 손실은 MWh당 1000달러라 하자. 이 때 예비력 제공량을 결정하는 문제는 아래와 같다.
Min. $10 P_A + 30 P_B + 0 R_A + 25 R_B + 0.05 (10 r_A + 30 r_B + 1000 L^{shed})$
Subject to
$r_A \leq R_A$
$r_B \leq R_B$
$ P_A + P_B = 130$ : $\lambda_P$
$ P_A + R_A \leq 100$
$ P_B + R_B \leq 100$
$ r_A + r_B + L^{shed} = 20 $
$P_A, P_B, R_A, R_B, r_A, r_B, L^{shed} \geq 0$
위에서 $r_A$와 $r_B$는 총 수요가 20 MW 증가할 경우에 각 발전기의 출력 증가량이고, $ L^{shed}$는 증가한 수요 중 충족하지 못한 양이다.
이 문제를 풀어 얻는 $R_A + R_B$가 예비력 제공량이다. 수요 증가 확률 및 공급 부족에 의한 손실이 얼마나 큰가에 따라, 최적의 예비력 제공량은 20 MW 일 수도, 그보다 작을 수도, 아예 0일 수도 있다.
Stochastic market clearing 시의 매출 계산
Stochastic market clearing 문제에서 하루전 시장 수요-공급 일치 조건의 (bus $n$에서의) dual variable을 $\lambda_n^{D}$라 하자. 그러면 하루전 시장에서의 가격은 $\lambda_n^{D}$이다.
한편 실시간 시장에서 시나리오 $\omega$ 하에 수요-공급 일치 조건의 dual variable을 $\gamma_{n \omega}$라 하자. 그리고 시나리오 $\omega$의 확률을 $\pi_{\omega}$라 하자. 그러면 해당 시나리오 하에 실시간 시장에서의 가격은 $\pi_{\omega}$이다.
하루전 시장과 실시간 시장에서의 총 매출은, 하루전 시장에서 계획된 에너지 판매량을 $E$, 실시간 시장에서 시나리오 $\omega$ 하에 balancing을 위해 ‘추가적으로’ 판매하거나 수요처인 경우 소비를 줄인 에너지를 $\Delta E_{\omega}$라 할 때 아래와 같이 계산된다.
$\lambda_n^{D} E + (\gamma_{n \omega}/\pi_{\omega}) \Delta E_{\omega}$
$\gamma_{n \omega}$를 $\pi_{\omega}$로 나눠주는 이유는, 하루전 시장과 실시간 시장을 모두 포함하는 최적화 문제에서는 각 시나리오 별 subproblem의 목적함수에 이미 $\pi_{\omega}$가 곱해져 있으므로, dual variable이 ‘$\pi_{\omega}$만큼 scaling된’ sensitivity이기 때문이다.
($E$가 음수면 에너지를 소비한 것, $\Delta E$가 음수면 발전량을 줄이거나 에너지를 추가로 소비한 것이다.)
실시간 시장에서 각 참가자들의 수익
하루전 시장에서의 market clearing price를 $\lambda^{S}$, 실시간 시장에서의 market clearing price를 $\lambda^{B}$라 하자.
만약 실시간 시장에서의 total ‘net’ demand (총 부하에서 재생발전을 뺀 ‘순’부하) 가 ‘계획된’ 급전발전량을 초과하면 (즉 excess consumption이면), 도출된 market clearing price들에 대해 $\lambda^{B} \geq \lambda^{S}$ 가 성립한다.
또한 하루전 시장에서와 실시간 시장에서의 순부하를 각각 $P_N^{S}$와 $P_N^{B}$라 할 때, 급전가능 발전기들은 전일시장에서 총합 $P_N^{S}$만큼의 전력을 공급하기로 계획되었을 것이므로, 실시간 시장에서 급전가능 발전기들이 추가로 얻는 총 매출은 $(P_N^{B}-P_N^{S}) \lambda^{B} > 0$ 이다.
이 때 각각의 재생 (즉 급전불가능) 발전기 $j$가 실시간 시장에서 얻는 매출은 얼마일까?
재생발전기 $j$가 하루전 시장에서 예상한 발전량을 $P_{Uj}^{S}$, 실시간 시장에서의 실제 발전량을 $P_{Uj}^{B}$라 하자. 그러면 실시간 시장에서의 매출은 $(P_{Uj}^{B} - P_{Uj}^{S}) \lambda^{B}$ 이다.
만약 재생발전기 $j$가 ‘하루전 시장에서 예상된 발전량 대비’ 실제로 더 적게 발전했다면, 즉 $P_{Uj}^{B} < P_{Uj}^{S}$ 라면, 매출은 음수이다.
이를 ‘급전발전기로부터 $(P_{Uj}^{B} - P_{Uj}^{S})$ 만큼의 전력을 구입해서 계획된 발전량을 맞추는 것’으로 해석한다면, $\lambda^{B} \geq \lambda^{S}$ 이므로 ‘실시간 시장에서 하루전 시장 대비 더 비싼 가격으로 전기를 구입하는’ penalty를 감수하는 셈이다. 이 penalty는 ‘재생발전기 $j$가 excess consumption을 악화시키는 역할을 했으므로’ 받는 것으로 해석할 수 있다.
반대로 재생발전기 $j$가 ‘하루전 시장에서 예상된 발전량 대비’ 실제로 더 많이 발전했다면, 즉 $P_{Uj}^{B} > P_{Uj}^{S}$ 라면, 매출은 양수이다.
이는 ‘실시간 시장에서 $(P_{Uj}^{B} - P_{Uj}^{S})$ 만큼의 전력을 하루전 시장 대비 더 비싼 가격으로 판매하는’ advantage를 얻는 셈이다. 이 advantage는 ‘재생발전기 $j$가 (비록 자기의지는 아니지만) excess consumption을 해소하는 역할을 했으므로’ 얻는 것으로 해석할 수 있다.
한편 수요처 $k$에서도 하루전 시장에서 계획한 부하 $P_{Dk}^{S}$와 실시간 시장에서의 실제 부하 $P_{Dk}^{B}$가 서로 다를 수 있다. 그러면 실시간 시장에서 지불해야 하는 금액은 $(P_{Dk}^{B} - P_{Dk}^{S}) \lambda^{B}$ 이다.
만약 수요처 $k$가 ‘하루전 시장에서 계획된 부하 대비’ 실제로 더 많은 에너지를 소비했다면, 즉 $P_{Dk}^{B} > P_{Dk}^{S}$ 라면, 지불해야 하는 금액은 양수이다.
이는 부하 증가에 의한 추가적인 에너지를 ‘하루전 시장 대비 더 비싼 가격으로 구매하는’ penalty를 감수하는 셈이다. 이 penalty는 ‘부하 $k$가 excess consumption을 악화시키는 역할을 했으므로’ 받는 것으로 해석할 수 있다.
반대로 수요처 $k$가 ‘하루전 시장에서 계획된 부하 대비’ 실제로 더 적은 에너지를 소비했다면, 즉 $P_{Dk}^{B} < P_{Dk}^{S}$ 라면, 지불해야 하는 금액은 음수이다.
이는 부하 감소에 의한 잉여 에너지를 ‘하루전 시장 대비 더 비싼 가격으로 판매하는’ advantage를 얻는 셈이다. 이 advantage는 ‘부하 $k$가 excess consumption을 해소하는 역할을 했으므로’ 얻는 것으로 해석할 수 있다.
지금까지의 논의와 반대로, 만약 실시간 시장에서의 total ‘net’ demand (총 부하에서 재생발전을 뺀 ‘순’부하) 가 ‘계획된’ 급전발전량보다 적으면 (즉 excess production이면), 도출된 market clearing price들에 대해 $\lambda^{B} \leq \lambda^{S}$ 가 성립한다.
이 경우 급전가능 발전기들이 하루전 시장 대비 출력을 줄임으로써 시장에 되돌려줘야 하는 금액의 총 합은 $(P_N^{S}-P_N^{B}) \lambda^{B} > 0$ 이다.
재생발전기 $j$가 ‘하루전 시장에서 예상된 발전량 대비’ 실제로 더 적게 발전했다면, 실시간 시장에서의 매출 $(P_{Uj}^{B} - P_{Uj}^{S}) \lambda^{B}$ 은 음수이다.
이는 실시간 시장으로부터 $(P_{Uj}^{B} - P_{Uj}^{S})$ 만큼의 전력을 ‘더 저렴한 가격으로’ 구매하는 advantage를 얻는 셈이다. 이 advantage는 ‘재생발전기 $j$가 (비록 자기의지는 아니지만) excess production을 해소하는 역할을 했으므로’ 얻는 것으로 해석할 수 있다.
반대로 재생발전기 $j$가 ‘하루전 시장에서 예상된 발전량 대비’ 실제로 더 많이 발전했다면, 실시간 시장에서의 매출 $(P_{Uj}^{B} - P_{Uj}^{S}) \lambda^{B}$ 은 양수이다.
이는 실시간 시장에서 $(P_{Uj}^{B} - P_{Uj}^{S})$ 만큼의 잉여전력을 ‘더 낮은 가격에’ 판매하는 penalty를 감수하는 셈이다. 이 penalty는 ‘재생발전기 $j$가 excess production을 악화시키는 역할을 했으므로’ 받는 것으로 해석할 수 있다.
한편 수요처 $k$가 실시간 시장에서 지불해야 하는 금액은 $(P_{Dk}^{B} - P_{Dk}^{S}) \lambda^{B}$ 이다.
만약 수요처 $k$가 ‘하루전 시장에서 계획된 부하 대비’ 실제로 더 많은 에너지를 소비했다면, 즉 $P_{Dk}^{B} > P_{Dk}^{S}$ 라면, 지불해야 하는 금액은 양수이다.
이는 부하 증가에 의한 추가적인 에너지를 ‘하루전 시장 대비 더 저렴한 가격으로 구매하는’ advantage를 얻는 셈이다. 이 penalty는 ‘부하 $k$가 excess production을 해소하는 역할을 했으므로’ 받는 것으로 해석할 수 있다.
반대로 수요처 $k$가 ‘하루전 시장에서 계획된 부하 대비’ 실제로 더 적은 에너지를 소비했다면, 즉 $P_{Dk}^{B} < P_{Dk}^{S}$ 라면, 지불해야 하는 금액은 음수이다.
이는 부하 감소에 의한 잉여 에너지를 ‘하루전 시장 대비 더 비싼 가격으로 판매하는’ penalty를 감수하는 셈이다. 이 advantage는 ‘부하 $k$가 excess production을 악화시키는 역할을 했으므로’ 얻는 것으로 해석할 수 있다.
재생발전의 merit-order effect
태양광/ 풍력 등 재생발전원은 일단 설치되었다면 일반적으로 ‘1단위의 전기를 더 생산하기 위한 marginal cost’가 거의 zero이다.
그러므로 급전 시 최우선순위를 부여받고, marginal cost가 상대적으로 작은 급전가능 발전기들로도 net demand를 충당할 수 있게 된다. Marginal cost가 높은 급전가능 발전기들의 순위는 밀리게 된다.
그 결과, 재생발전 비중이 증가할수록 전력 도매가격이 하락하는데, 이를 merit-order effect라 한다.
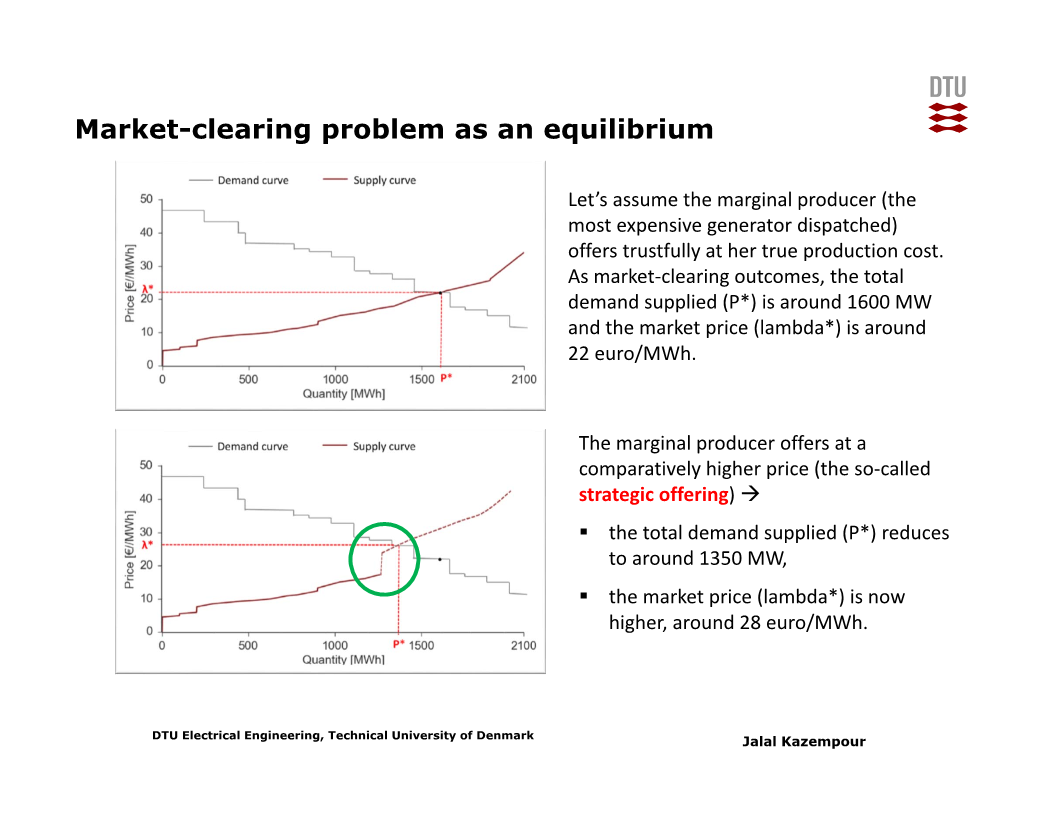
한편 재생발전 비중이 높으면 수요-공급 곡선에서 공급곡선 위치의 불확실성이 증가하므로, 이에 따라 수요곡선과 공급곡선이 만나는 점 및 시장가격의 불확실성도 증가한다.
Flexible demand의 수리모델
Flexible demand란, ‘일정 범위 내에서’ 전기 소비량을 결정할 수 있으며, 하루전 시장에서 계획된 부하를 실시간 시장에서 능동적으로 변경할 수 있는 전기 수요를 말한다.
Flexible demand $k$에 대해, 하루전 시장에서 $t$시에 대해 계획된 부하를 $d_k(t)$, 실시간 시장에서 stochasticity scenario $\omega$가 실현된 경우의 실제 부하를 $d_{k \omega}(t)$, 계획된 부하 대비 실제 부하를 증가시킬 경우 (발전기로 치면 down-regulation) 그 증가분을 $c_{k \omega}^{D}(t)$, 계획된 부하 대비 실제 부하를 감소시킬 경우 (발전기로 치면 up-regulation) 그 감소분을 $c_{k \omega}^{U}(t)$ 라 하자.
그리고 각 시간별로 flexible demand $k$의 $t$시 부하의 하한과 상한을 각각 $D_k^{min}(t)$ 와 $D_k^{max}(t)$, ‘하루 동안에 최소로 공급되어야 하는 총 에너지’를 $E_k^{day}$라 하자.
그러면, 아래 수식들이 성립한다.
$d_{k \omega}(t) = d_k(t) + c_{k \omega}^{D}(t) - c_{k \omega}^{U}(t) $
$0 \leq c_{k \omega}^{D}(t) \leq D_k^{max}(t) - d_k(t)$
$0 \leq c_{k \omega}^{U}(t) \leq d_k(t) - D_k^{min}(t) $
$\sum_{t=1}^T d_{k \omega}(t) \geq E_k^{day} $
만약 발전기의 ramping limit처럼 flexible demand에서도 1시간 동안 감소시키거나 증가시킬 수 있는 부하량 각각의 상한이 $D_k^{D}$와 $D_k^{U}$로 존재한다고 하면, 아래 수식들도 성립한다.
$ d_{k \omega}(t) - d_{k \omega}(t-1) \leq D_k^{U}$
$ d_{k \omega}(t-1) - d_{k \omega}(t) \leq D_k^{D}$
Flexible demand의 최적의 스케줄 도출을 위해서는 목적함수에 flexible demand에 대한 term들을 추가해야 한다. 이 때 해당 flexible demand가 전기를 공급받아서 얻는 ‘효용 (utility)’, 그리고 실시간 시장에서 부하를 조정해서 얻는 효용을 반영해야 한다.
해당 flexible demand가 단위 전기를 공급받을 때 얻는 효용을 $U_k(t)$, 실시간 시장에서 부하를 늘릴 때 (down-regulation)와 줄일 때 (up-regulation) 얻는 효용을 각각 $U_k^{D}(t)$와 $U_k^{U}(t)$라 하자. 그리고 시나리오 $\omega$의 확률을 $\pi_{\omega}$라 하자.
그러면 flexible demand가 얻는 총 효용은 아래와 같다.
\begin{align} \sum_{t=1}^T \lbrace U_k(t) d_k(t) + \sum_{\omega} \pi_{\omega} [U_k^{D}(t) c_{k \omega}^{D}(t) - U_k^{U}(t) c_{k \omega}^{U}(t)] \rbrace \notag \end{align}
Flexible demand 예시: Thermal comfort를 고려한 열부하의 전기 사용량
Demand response (DR) 모델링 시, 수요처가 부하로부터 얻는 ‘효용 (utility)’과 부하를 줄여서 얻는 보상을 비교해서 DR 스케줄을 결정하게 된다.
건물에서 냉난방기기를 제어해 DR을 수행할 경우, 주로 실내온도의 함수로 주어지는 ‘thermal comfort’를 효용으로 둔다. 즉 대상 건물에서 시간별로 가장 선호되는 기준 실내온도를 정한 후, 실제 실내온도가 기준온도에서 많이 벗어날수록 효용이 적다고, 즉 thermal ‘dis’comfort가 크다고 본다.
시간 $t$에서의 기준 실내온도를 $\hat{x}^{i}_t$, 실제 실내온도를 $x^{i}_t$로 두자. 그러면, ‘기준온도보다 높아도 낮아도 효용이 줄어드는’ 것을 고려해 목적함수의 thermal discomfort term을 $\sum_{t} c (x^{i}_t - \hat{x}^{i}_t)^2$ 로 둘 수 있다 ($c$는 comfort의 가치를 반영하는 계수이며, $c$가 클수록 comfort를 중요하게 생각한다).
목적함수에는 thermal discomfort term 뿐 아니라, 건물 온도를 기준 온도에 가깝게 유지하는 데 드는 에너지 요금도 포함되어야 한다. 그래야 thermal comfort와 에너지 사용 간 trade-off를 구할 수 있기 때문이다.
해당 건물이 난방을 전기온수보일러로 수행하고, 전기온수보일러의 시간 $t$에서의 전기 소비량 $u_t$와 온수탱크 내 온도 $x^{w}_t$ 및 실내온도 $x^{i}_t$ 간의 관계를 아래와 같은 linear state-space model로 나타낼 수 있다고 하자.
\begin{align} \begin{bmatrix} x^{i}_{t+1} \newline x^{w}_{t+1} \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} \newline 0 & a_{22} \end{bmatrix} \begin{bmatrix} x^{i}_{t} \newline x^{w}_{t} \end{bmatrix} + \begin{bmatrix} 0 \newline b_2 \end{bmatrix} u_t \notag \end{align}
그러면 최적화 문제는, 위 linear state-space model을 제약조건으로 하고 아래의 항을 목적함수로 하는 quadratic programming problem이 된다.
$ \sum_{t} c (x^{i}_t - \hat{x}^{i}_t)^2 + \lambda^{R}_t u_t$
여기서 $\lambda^{R}_t$는 시간 $t$에서의 사용량요금이다.