논문 소개: Virtual power plant의 하루전시장 입찰 결정 (stochastic programming 기반)
Virtual power plant (VPP, 가상발전소) 는 급전가능발전원 (가스터빈 등), 급전불가능발전원 (태양광/ 풍력 등), 에너지저장장치 (배터리/ 양수발전 등) 등 여러 발전/ 전력저장 설비들을 클라우드 등 IT기술 기반으로 한꺼번에 제어해 단일 주체로써 전력시장에 입찰하는 방법이다.
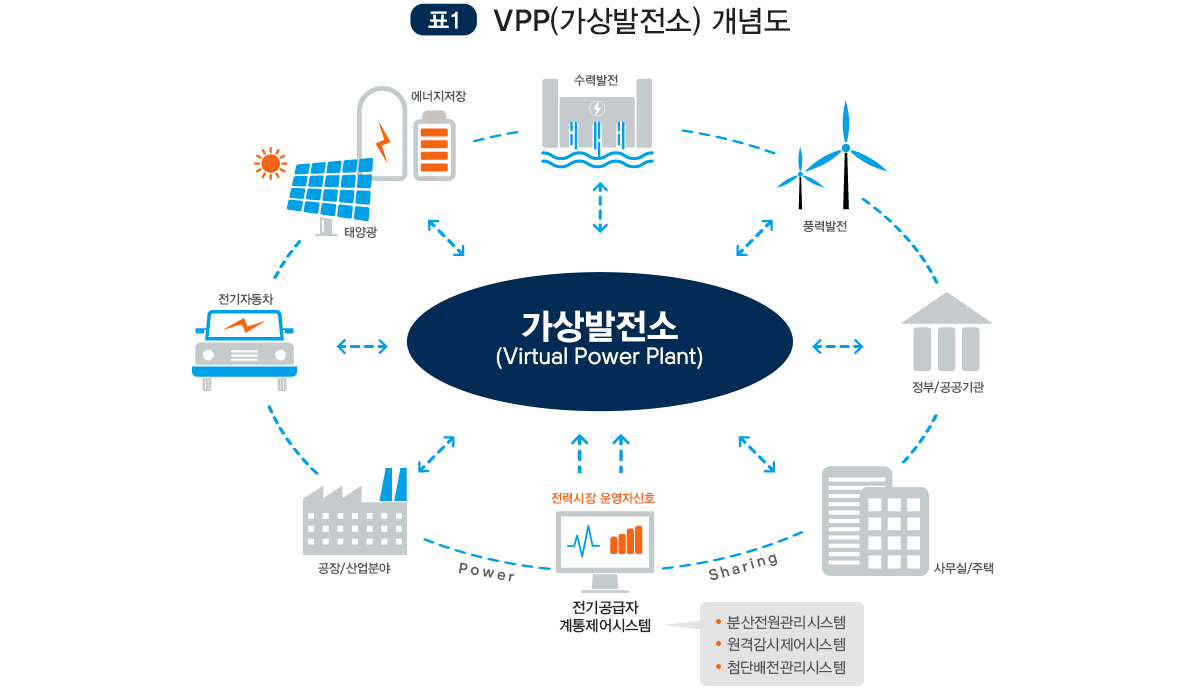 가상발전소 개념도. (출처: 한국전기연구원)
가상발전소 개념도. (출처: 한국전기연구원)
VPP를 통해 다수의 분산전원 사업자들이 보다 쉽게 전력시장에 참여할 수 있고, 급전가능발전원 및 에너지장치를 포함시켜 공급 당일 실제 발전량을 하루전 시장에서의 입찰 전력량과 일치시킬 수 있으며, 필요시 VPP 전체가 주파수 변동 억제 등의 계통안정도 관련 보조서비스를 제공할 수도 있다.
이 포스팅에서는, VPP가 하루전시장과 실시간시장으로 이루어진 전력시장에 입찰 시 시간별 발전량을 결정하는 방법에 대한 대표적 논문을 소개한다. Applied Energy에서 2013년에 출판된 “Offering model for a virtual power plant based on stochastic programming” 이다.
경제성 관점에서 VPP의 필요성
VPP가 하루전시장과 실시간시장으로 이루어진 전력시장에 입찰할 경우, 하루전시장에 ‘내일 24시간의 각 시간 별 발전량’ 을 제출한다. VPP는 급전 당일에 재생발전원의 실제 발전량을 관측하고 급전가능발전원과 에너지저장장치를 제어하여, 총 발전량이 하루전시장에 제출했던 시간별 발전량과 일치하도록 한다 (balancing).
그러나, 만약 재생발전원의 용량은 큰데 급전가능발전원 및 에너지저장장치가 부족하거나 심지어는 없다면, 공급 당일의 총 발전량이 하루전에 제출된 발전량과 다를 것이다. 이러한 차이는 경제적 손실을 야기한다.
이를테면 특정 시간에 대해 하루전 제출된 급전량은 큰데 풍력발전량이 예상보다 너무 낮아서, 가스터빈을 최대출력으로 가동하고 에너지저장장치를 최대로 방전시켜도 하루전 제출된 발전량보다 부족할 수 있다. 이 경우 balancing을 위해 전력부족분을 실시간 시장에서 더 높은 가격에 구입하므로, 하루전시장에서 전력부족분만큼을 덜 입찰했을 경우와 비교하면 경제적 손실을 본다.
반대로 특정 시간에 대해 하루전 제출된 발전량은 작은데 풍력발전량이 예상보다 너무 높아서, 가스터빈을 가동하지 않고 에너지저장장치를 최대로 충전시켜도 하루전 제출된 발전량을 초과할 수 있다. 이 경우 balancing을 위해 잉여전력을 실시간 시장에서 더 낮은 가격에 판매하므로, 하루전시장에서 잉여전력분만큼을 더 입찰했을 경우와 비교하면 경제적 손실을 본다.
가상발전소는 이러한 ‘하루전에 제출된 발전량과 실제 발전량의 차이’를 줄여 수익을 증가시킬 수 있다. 재생발전원 단독으로는 아무리 예측을 잘 해도 하루전 제출 발전량과 실제 발전량 간에 차이가 있다. 이러한 차이가 실시간 시장에서의 balancing에 의한 경제적 손실을 야기하므로, 급전가능발전원 및 에너지저장장치와 연계해 그 차이를 없애고자 하는 것이다.
(이러한 차이를 줄일 경우, 국가적으로는 중앙급전 발전원들의 발전량을 보다 정확하게 산정할 수 있다는 편익도 있다.)
위 논문의 case study에서 다루는 가상발전소도 9.6MW급 풍력터빈에 더해 40MWh급 양수에너지저장소와 5.67MW급 급전가능 가스터빈으로 구성된다.
참고로 우리나라의 경우 아직 실시간 시장이 없으며, 현재 VPP의 수익원 대부분은 재생발전량을 정확하게 예측할 경우 받는 정산금이다. 그러나 실시간 시장이 2024년 2월부터 제주도에 시범적으로 개설되며 2025년에는 육지에도 적용될 예정이므로, 향후 몇 년 내로 VPP 사업이 활성화될 수 있을 것으로 보인다.
VPP의 offer curve: 급전량을 미래의 시장가격의 함수로 결정
하루전시장에 제출할 시간별 급전량을 최적화 문제를 풀어 결정하려면, 하루전 시장에서의 시간별 시장가격 및 실시간 시장에서의 시간별 시장가격을 알아야 한다 (VPP는 시장가격을 정해진 그대로 받아들이며 시장가격에 영향을 미치지 못하는 price taker라고 가정).
그러나 실제로는 다음날의 시간별 시장가격을 모르므로, ‘하루전 시장에서의 $t$시의 시장가격이 $\lambda(t)$이면 우리 VPP는 $G(t)$ 만큼 발전할 것’ 이라는 계획을 제출한다. 즉 시간별 발전량이 해당 시간의 시장가격의 함수이다. 이를 ‘offer curve’라 한다.
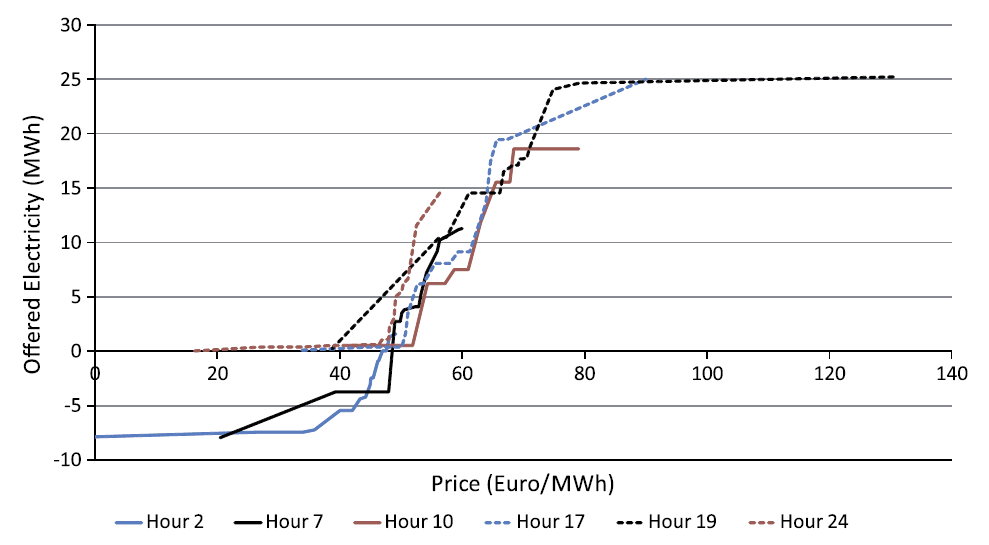 Offer curve (출처: 소개 논문).
Offer curve (출처: 소개 논문).
위 그림에서 각 curve는 하나의 시간에 대응하며, 해당 시간의 시장가격(가로축)에 대응하는 VPP의 발전량(세로축) 을 보여준다. 음의 발전량은 에너지저장장치 충전을 의미한다 (부하가 적어 상대적으로 시장가격이 저렴한 시간대에 충전 후 낮 시간에 방전한다).
불확실성을 고려한 stochastic programming 기반 offer curve 도출
여기서 난점은, 재생발전원의 다음날 시간별 발전량 또한 불확실하다는 것이다. 그러므로 ‘stochastic programming’ 문제가 된다.
보통 이러한 multi-period (여기서는 24시간) stochastic programming에서는, 다음날의 시간별 시장가격과 재생발전량 ‘시나리오’들을 아래와 같이 만든다.
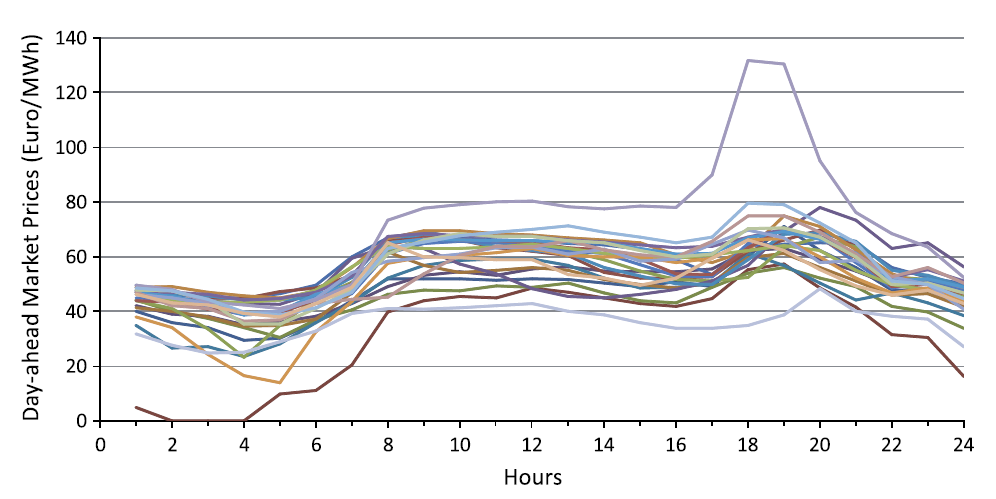
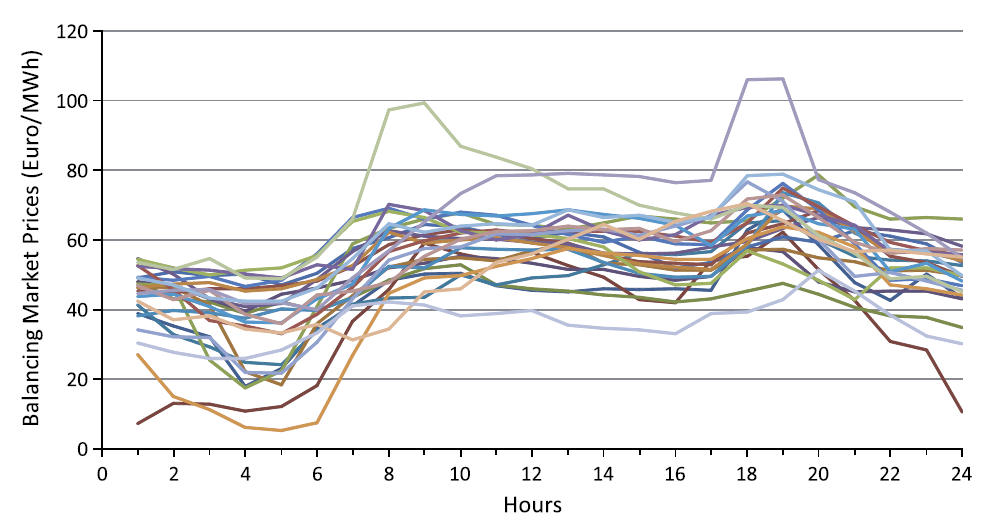 시간별 시장가격 시나리오 (위: 하루전시장, 아래: 실시간시장. 출처: 소개 논문).
시간별 시장가격 시나리오 (위: 하루전시장, 아래: 실시간시장. 출처: 소개 논문).
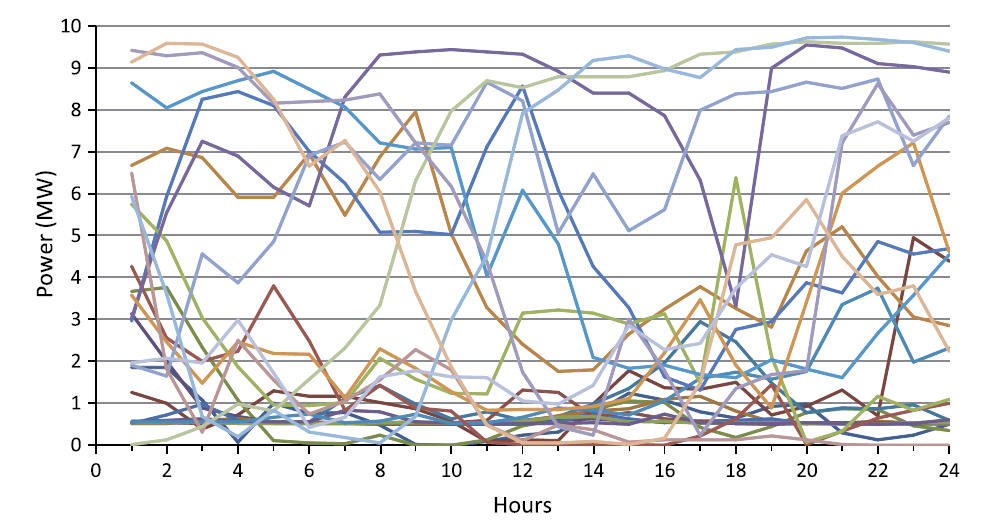 시간별 풍력 발전량 시나리오 (출처: 소개 논문).
시간별 풍력 발전량 시나리오 (출처: 소개 논문).
각 시나리오는 24시간 동안의 시간별 수치들의 집합 즉 ‘trajectory’이다. 이렇게 trajectory를 쓰는 이유는, 해당 시계열 데이터들이 시간에 따른 자기상관관계 (autocorrelation) 를 가질 것이기 때문이다.
또한 각 시나리오별 확률도 사전에 결정해야 한다 (해당 논문에서는 편의상 각 시나리오 별 확률이 같다고 (equiprobable) 가정했다).
시간별 시장가격의 시나리오 인덱스를 $p$, 풍력발전량의 시나리오 인덱스를 $w$라 하자. 최적화 문제에서는 ‘각 시나리오 별 하루전 시장에서의 시간 $t$에 대한 발전량 제출’ $G_{wp}(t)$를 결정한다.
실시간 시장에서의 balancing에 대한 제약조건은 아래와 같다.
$G_{wp}(t) = g_w(t) + g_{wp}^c (t) + g_{wp}^t (t) + bm_{wp}^{up}(t) - g_{wp}^p(t)/\eta - bm_{wp}^{down}(t) \quad \forall w,p,t$
각 시간 $t$에 대해 어떤 시나리오 $wp$ 하에서도, $G_{wp}(t)$는 당일의 풍력 발전량 $g_w(t)$, 가스터빈 발전량 $g_{wp}^c (t)$, 양수에너지저장소의 터빈에 의한 발전량 $g_{wp}^t (t)$, 당일 시장에서 필요 시 추가로 구입하는 에너지 $bm_{wp}^{up}(t) $ 의 합으로부터, 양수에너지저장소의 펌프 가동 에너지 $g_{wp}^p (t)$ 에 efficiency factor $\eta$를 곱한 값과 당일 시장에서 필요 시 재판매하는 에너지 $bm_{wp}^{down}(t) $ 을 뺀 값과 같아야 한다.
그런데, offer curve에서 시간별 급전량은 시장가격의 함수이기는 하지만 풍력발전량의 함수는 아니다. 다음날의 풍력발전량을 ‘모르는’ 상태에서 시간별 급전량을 동일시간의 시장가격의 함수로 결정하기 때문이다. 그러므로, 하나의 $(p,t)$ 순서쌍이 주어지면 $G_{wp}(t)$는 모든 $w$에 대해 같아야 한다. 즉, 아래 제약조건이 추가로 필요하다.
$G_{w_{1} p}(t) = G_{w_{2} p}(t) = \cdots = G_{w_{n} p}(t)$ ($w_1, \dots,w_n$은 풍력발전 시나리오들)
Stochastic programming에서는 위 수식처럼 여러 시나리오들에 대해 변수가 같다는 제약조건을 ‘non-anticipativity constraint’ 라고 한다. Anticipate가 ‘예측하다’ 라는 뜻인데, 여기서는 다음날의 풍력발전을 정확히 예측하지 못한다는 의미이다.
그 외의 제약조건들은 필자의 최적화문제 소개글들에 있는 출력조정 제약, 에너지저장장치 충방전에 대한 제약 등이다.
목적함수는 아래와 같다. $\pi$는 시나리오 별 확률을 의미하며, 각 시나리오 별 총 수익은 하루전 시장에서의 입찰에 의한 수익 $\lambda_p(t)G_{wp}(t)$에 실시간 시장에서 balancing을 위해 추가적으로 판매하는 잉여전력의 수익 및 추가적으로 구입하는 전력부족분의 비용 (음의 수익) 을 더하고 가스터빈 구동에 드는 연료비 $C_{wp}^c(t)$ 및 시동비용 $SUC^c v_{wp}^c (t)$ 를 뺀 값이다.
$ \sum_t \sum_w \pi_w \sum_p \pi_p \sum_{r^{down}} \pi_r^{down} \sum_{r^{up}} \pi_r^{up} [\lambda_p(t) (G_{wp}(t) + bm_{wp}^{down}(t) \psi_r^{down}(t) - bm_{wp}^{up}(t) \psi_r^{up}(t) ) - C_{wp}^c(t) - SUC^c v_{wp}^c (t)] $
문제를 풀면, 위 시나리오들을 고려할 때의 ‘총 수익의 기대값’을 최대화하도록 offer curve가 결정된다.
위 연구는 stochastic programming 기반으로 재생발전 비중이 높은 VPP의 입찰량을 계산하는 방법의 baseline으로써 가치가 있다 (해당 논문은 인용횟수가 300회를 넘는다).