건물의 시간별 전기부하 학습 후 예측하기 - 딥러닝을 쓴다면?
지난 포스팅에서는, 건물의 시간별 전기부하 추정 문제에서 딥러닝이 아닌 ‘전통적인’ 선형회귀로도, 적절한 모델 구성 시 adjusted $R^2$ 0.95 이상의 우수한 성능을 얻을 수 있음을 보였다. 그렇다면, 딥러닝으로는 어떨까?
Dense Neural Net
전기부하 데이터는 시계열 데이터이므로 Recurrent Neural Network (RNN) 을 쓸 수 있으나, 먼저 단순한 Dense Neural Network (DNN) 을 사용해 보자.
이 경우 지난 포스팅의 선형회귀와 제대로 비교하기 위해서는, 선형회귀에서처럼 유형별 sub모델 4개를 만들고 predictor들도 교차항을 제외하면 선형회귀에서와 똑같이 두어야 한다. 즉, 일유형 dummy, 월별 dummy, 시간별 dummy를 두어야 한다.
(교차항은 빼도 된다. NN이 제대로 적합된다면 기온/조도와 월/시간의 상호관계까지 고려한 전기부하 간의 적절한 nonlinear function을 ‘알아서 잘’ 찾아줄 것이므로.)
여기서는 DNN은 2개의 Dense layer로 이루어져 있고 첫 layer의 node는 20개, 두 번째 layer의 node는 10개로 둔다. 훈련 epoch 수는 1000이고, optimizer는 특별한 이슈가 없으므로 가장 일반적인 Adam을 쓴다.
구체적인 코드는 아래와 같다 (전기부하 데이터를 최대값이 1 근처가 되게 scaling하였음에 주의한다. Scaling하지 않으면 적합 결과가 상수함수가 되어 전혀 추정을 하지 못한다).
(GitHub Repo 링크)
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow import keras
### Dataset 불러오기 (DNN은 여름평일/ 겨울평일/ 봄가을평일/ 휴일 각각에 대해 data 파일 별도로 구성함)
workday_springfall_train = np.loadtxt("I_train.txt")
workday_summer_train = np.loadtxt("II_train.txt")
workday_winter_train = np.loadtxt("III_train.txt")
holiday_train = np.loadtxt("IV_train.txt")
workday_springfall_test = np.loadtxt("I_test.txt")
workday_summer_test = np.loadtxt("II_test.txt")
workday_winter_test = np.loadtxt("III_test.txt")
holiday_test = np.loadtxt("IV_test.txt")
actualpower = np.loadtxt("actualusage.txt")
### DNN layer 설정 함수
n_node_firstlayer = 20
n_node_secondlayer = 10
n_epochs = 1000
def model_dnn():
model = keras.models.Sequential([
keras.layers.Dense(n_node_firstlayer,activation="sigmoid"),
keras.layers.Dense(n_node_secondlayer,activation="sigmoid"),
keras.layers.Dense(1,activation="linear") # 계측형 데이터 예측이므로 마지막 층은 node 1개, activation은 linear
])
return model
### 훈련 및 예측 실행 함수
def model_train_pred(data_train, data_test, modelname):
response_train = data_train[:,1].reshape(-1,1)/1000 # [0,1] 구간즈음에 들어오게 scaling해야 함, 그렇지 않고 원본 쓰면 제대로 fit 안되고 대표값 1개만 반환함
features_train = data_train[:,2:]
hourindex_train = data_train[:,0].reshape(-1,1)
# response_test = data_test[:,1].reshape(-1,1)/1000
features_test = data_test[:,2:]
hourindex_test = data_test[:,0].reshape(-1,1)
model = model_dnn()
checkpoint_cb = keras.callbacks.ModelCheckpoint("./"+modelname+".h5",monitor='loss',save_best_only=True) # monitor까지 해 줘야 파일이 저장됨
model.compile(loss="mse",optimizer="adam") # 계측형 데이터 예측이므로 loss function은 mse
history = model.fit(features_train,response_train,epochs=n_epochs,callbacks=[checkpoint_cb])
y_fit = model.predict(features_train)
y_pred = model.predict(features_test)
return y_fit, y_pred, hourindex_train, hourindex_test
### 여름평일/ 겨울평일/ 봄가을평일/ 휴일 각각에 대해 모델 훈련 및 예측
[y_fit_workday_summer, y_pred_workday_summer,
hourindex_workday_summer_train,
hourindex_workday_summer_test] = model_train_pred(workday_summer_train,
workday_summer_test,
"dnn_workday_summer")
[y_fit_workday_winter, y_pred_workday_winter,
hourindex_workday_winter_train,
hourindex_workday_winter_test] = model_train_pred(workday_winter_train,
workday_winter_test,
"dnn_workday_winter")
[y_fit_workday_springfall, y_pred_workday_springfall,
hourindex_workday_springfall_train,
hourindex_workday_springfall_test] = model_train_pred(workday_springfall_train,
workday_springfall_test,
"dnn_workday_springfall")
[y_fit_holiday, y_pred_holiday,
hourindex_holiday_train,
hourindex_holiday_test] = model_train_pred(holiday_train,
holiday_test,
"dnn_holiday")
### 원래 시간 순서대로 데이터 재정렬
def aggregate(y_workday_summer, y_workday_winter, y_workday_springfall, y_holiday,
hourindex_workday_summer, hourindex_workday_winter, hourindex_workday_springfall, hourindex_holiday):
hourlypower = np.zeros((8760,))
for k in range(y_workday_summer.shape[0]):
hourlypower[int(hourindex_workday_summer[k][0]-1)] = y_workday_summer[k]
for k in range(y_workday_winter.shape[0]):
hourlypower[int(hourindex_workday_winter[k][0]-1)] = y_workday_winter[k]
for k in range(y_workday_springfall.shape[0]):
hourlypower[int(hourindex_workday_springfall[k][0]-1)] = y_workday_springfall[k]
for k in range(y_holiday.shape[0]):
hourlypower[int(hourindex_holiday[k][0]-1)] = y_holiday[k]
return hourlypower*1000 # scale 원래대로
fittedpower = aggregate(y_fit_workday_summer, y_fit_workday_winter, y_fit_workday_springfall, y_fit_holiday,
hourindex_workday_summer_train, hourindex_workday_winter_train, hourindex_workday_springfall_train, hourindex_holiday_train)
predictedpower = aggregate(y_pred_workday_summer, y_pred_workday_winter, y_pred_workday_springfall, y_pred_holiday,
hourindex_workday_summer_test, hourindex_workday_winter_test, hourindex_workday_springfall_test, hourindex_holiday_test)
### 모델 평가
def adjrsq(actual,estimate,k):
bary = np.mean(actual)
SST = np.sum((actual - bary)**2)
SSR = np.sum((actual - estimate)**2)
r = 1 - (SSR/(8760-k-1))/(SST/(8760-k))
return r
adjRsq_train = adjrsq(actualpower[:,0],fittedpower,workday_summer_train[:,2:].shape[1]-2)
adjRsq_test = adjrsq(actualpower[:,1],predictedpower,workday_summer_test.shape[1]-2)
print(adjRsq_train)
print(adjRsq_test)
plt.plot(actualpower[:,0])
plt.plot(fittedpower)
plt.show()
plt.plot(actualpower[:,1])
plt.plot(predictedpower)
plt.show()
Adjusted $R^2$를 계산해보면 훈련 set에 대한 값은 0.9402이다. 이는 Weighted Least square (WLS) 만 했을 때의 결과인 0.9220보다는 더 높지만, WLS 잔차에 대한 SARMA 보조회귀모델 적합까지 추가 수행 시 결과인 0.9735보다는 낮다. 한편 검증 set에 대한 값은 0.8375로, WLS만 했을 때의 결과인 0.8706보다도 낮다.
딥러닝 특성상 수행 시 마다 결과가 조금씩 달라지므로 여러 번 계산해 보았으나, 어떤 경우에도 DNN이 검증 set에서 WLS보다 좋은 결과를 보이지 못했다.
검증 set에 대한 결과와 딥러닝 훈련에 드는 계산비용을 생각하면, 딥러닝이 우월하다고 볼 수 없다 (계산 시간만 따져도 몇 분 vs. 몇 초 (WLS만 수행 시)).
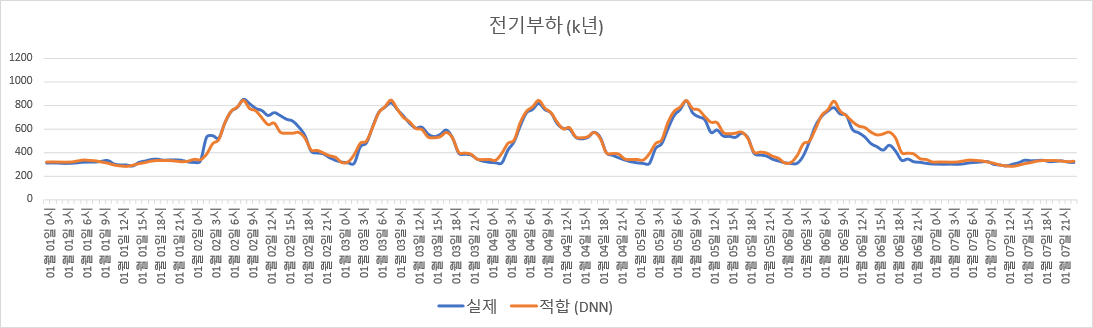
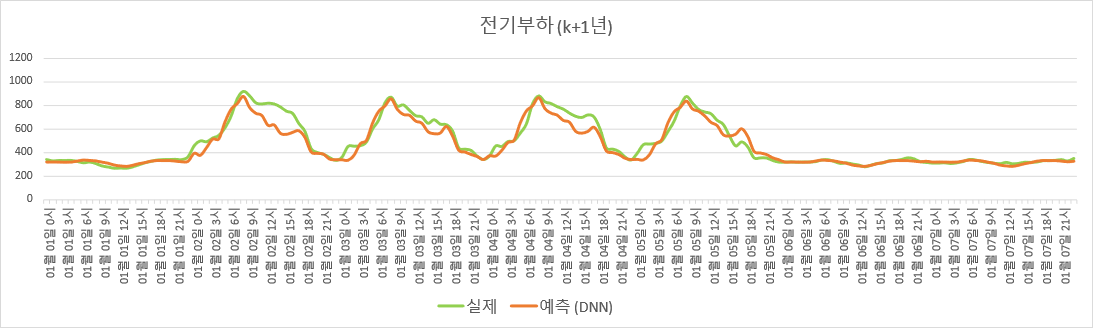 $K$년도 데이터로 적합한 DNN 모델 기반 전기부하 추정.
$K$년도 데이터로 적합한 DNN 모델 기반 전기부하 추정.
Recurrent Neural Net
그럼, RNN을 쓰면 어떨까?
RNN의 경우 이전 시간의 전기 부하가 predictor로 포함되는 구조이므로, 일 유형별로 sub모델을 4개 만들 수는 없다. 1번째 시간의 data point부터 8,760번째 시간의 point까지 연속적으로 모델에 흘러들어가야 하므로, 하나의 모델로 모든 시간의 전기 부하를 예측해야 한다. 그러므로 RNN의 predictor로는 일 유형(평일/휴일) dummy도 추가한다.
Layer 수와 node 수는 DNN에서와 같게 둔다. DNN에서 그래도 선형회귀와 비슷한 수준의 예측 성능을 보였으므로, layer 수와 node 수 결정이 잘못된 것은 아니라 판단했다.
코드는 아래와 같다.
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow import keras
### Dataset 불러오기
data_train = np.loadtxt("RNN_train.txt")
data_test = np.loadtxt("RNN_test.txt")
n_node_firstlayer = 20
n_node_secondlayer = 10
n_epochs = 1000
optimizer = keras.optimizers.Adam(lr=0.001,beta_1=0.9,beta_2=0.999)
response_train = data_train[:,0].reshape(1,-1) / 1000 # scaling
features_train = data_train[:,1:].reshape(1,-1,37) # reshape 해 줘야 rnn코드가 돌아감
response_test = data_test[:,0].reshape(1,-1) / 1000
features_test = data_test[:,1:].reshape(1,-1,37)
### RNN layer 설정 함수
model_rnn = keras.models.Sequential([
keras.layers.SimpleRNN(n_node_firstlayer,return_sequences=True,input_shape=[None,37]),
keras.layers.SimpleRNN(n_node_secondlayer,return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(1)) # To make a sequence-to-sequence model, TimeDistributed should be used
])
### 훈련 및 예측 실행 함수
checkpoint_cb_rnn = keras.callbacks.ModelCheckpoint("./rnn.h5",monitor='loss',save_best_only=True) # monitor까지 해 줘야 파일이 저장됨
model_rnn.compile(loss="mse",optimizer=optimizer)
history_rnn = model_rnn.fit(features_train,response_train,epochs=n_epochs,callbacks=[checkpoint_cb_rnn])
y_fit = (model_rnn.predict(features_train) * 1000).reshape(-1)
y_pred = (model_rnn.predict(features_test) * 1000).reshape(-1)
### 모델 평가
def adjrsq(actual,estimate,k):
bary = np.mean(actual)
SST = np.sum((actual - bary)**2)
SSR = np.sum((actual - estimate)**2)
r = 1 - (SSR/(8760-k-1))/(SST/(8760-k))
return r
adjRsq_train = adjrsq(data_train[:,0],y_fit,features_train.shape[2]-2)
adjRsq_test = adjrsq(data_test[:,0],y_pred,features_test.shape[2]-2)
print(adjRsq_train)
print(adjRsq_test)
plt.plot(data_train[:,0])
plt.plot(y_fit)
plt.show()
plt.plot(data_test[:,0])
plt.plot(y_pred)
plt.show()
plt.plot((data_test[:,0] - y_fit))
계산에 걸리는 시간은 수십 분으로, 당연히 DNN보다도 훨씬 길다. 그렇다면 적합 결과는?
Adjusted $R^2$를 계산해보면 훈련 set에 대한 값은 0.8880, 검증 set에 대한 값은 0.7936으로, 오히려 복잡한 모델을 썼음에도 성능이 더 떨어졌다. 심지어 훈련 set에 대해서조차 그렇다.
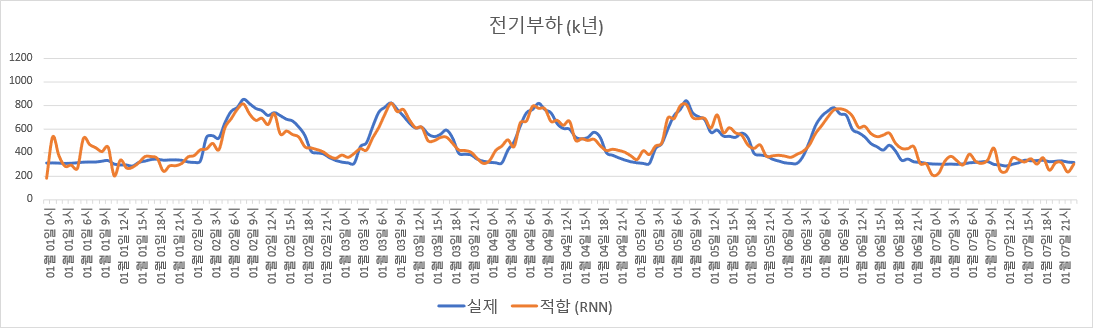
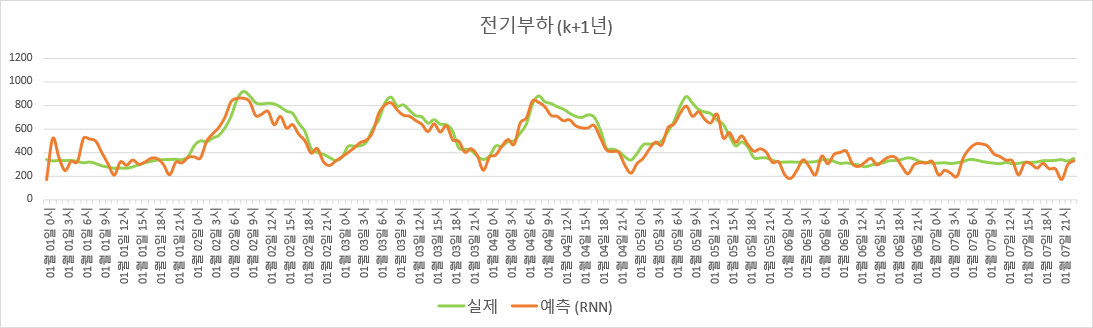 $K$년도 데이터로 적합한 RNN 모델 기반 전기부하 추정.
$K$년도 데이터로 적합한 RNN 모델 기반 전기부하 추정.
위 그림을 보면, RNN으로 추정한 부하 그래프가 매우 울퉁불퉁하다. 이는 Data Generating Process와 맞지 않는 모델을 사용한 것, 즉 mis-specification을 암시한다. (그러므로 RNN에 layer 또는 node를 추가하거나, 더 복잡한 방법인 LSTM/ GRU 등을 시도하는 것은 의미가 없다고 판단된다.)
실제로는, ‘그냥 무작정 RNN부터 쓰고 보는 사람’이라면 시간별/ 월별/ 일유형별 dummy variable 없이 온도와 조도만을 input으로 하여 신경망을 훈련시킬 가능성이 높다. 이 경우에 대해 adjusted $R^2$를 계산해 본 결과, 훈련 set에 대한 값은 0.2328, 검증 set에 대한 값은 0.1756으로, 전혀 엉뚱한 결과를 얻는다.
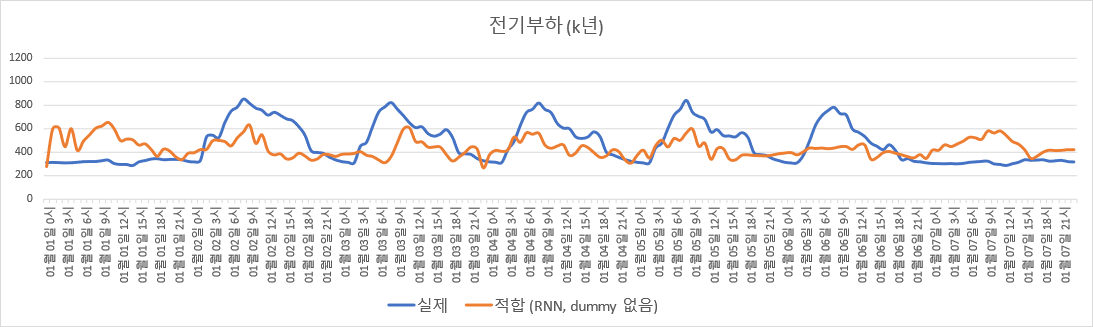
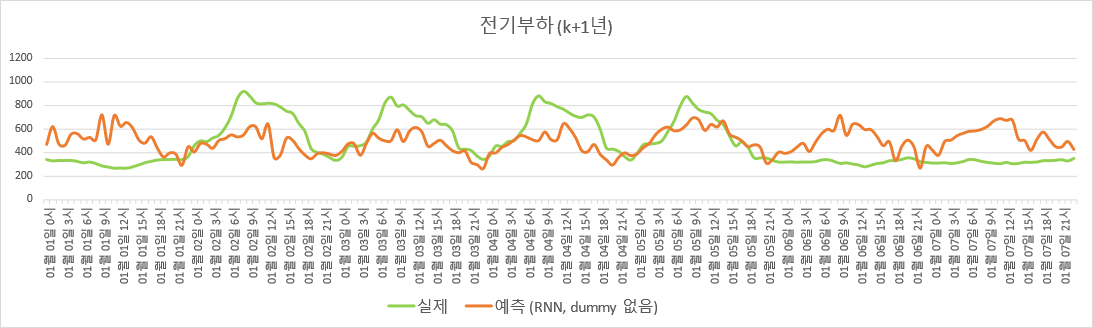 $K$년도 데이터로 적합한 RNN 모델 기반 전기부하 추정 (시간별/ 월별/ 일유형별 dummy variable 없이).
$K$년도 데이터로 적합한 RNN 모델 기반 전기부하 추정 (시간별/ 월별/ 일유형별 dummy variable 없이).
나가며
딥러닝이 음성인식과 자연어 처리에서 큰 진보를 이뤄내서 그런지, 이런 시계열 데이터 예측은 RNN으로 하면 다 해결될 거라 생각하는 경우가 많다.
그러나 간단한 선형회귀 모델도 잘 구성하면 NN보다 좋은 경우도 많고, 특히 RNN은 매우 복잡한 패턴이 stationary한 분포를 갖고 반복적으로 나타날 때 의미가 있지 (같은 나라/ 문법/ 분야 하의 문장들 등), 그렇지 않으면 계산 비용만 크게 소비하고 별 효과가 없다는 것은 계산과학 필드에서는 상식이다. 이러한 상식은 에너지 부하 데이터에 대해서도 마찬가지로 적용됨을 확인해 볼 수 있었다.
당장 이번 사례에서 선형회귀와 DNN에 대해 sub모델 4개를 구성한 것을 생각해 보면, 1년간의 시간별 부하 데이터는 non-stationary data이다. 이를 고려하지 않고 non-stationary data에 대해 무작정 단일한 RNN 모델을 쓰면, 결과가 이상하게 나올 수밖에 없다 (일유형 dummy변수를 추가하기는 했지만, 그것으로는 부족했다).
데이터의 non-stationarity를 고려해 sub모델 4개로 나누는 ‘데이터 전처리’와 오차의 자기상관성을 추가로 설명하는 과정을 거친 덕분에, 그리고 각 sub모델 별 구간 내의 non-linearity가 심하지 않았기에, 간단한 선형회귀 모델로 딥러닝보다 더 나은 결과를 빠르게 얻을 수 있었다. (거기에 더해, 선형회귀 모델은 딥러닝처럼 훈련 시마다 모델 parameter 값들이 다르게 나오지 않고 항상 같게 나온다는 장점도 있다.)
이렇듯 계산 시간도 빠르면서 성능도 나은 경우 ‘computational efficiency’가 좋다고 한다. 내가 가진 데이터에 대해 더 잘 알수록, 그리고 가능한 기법들 각각의 장단점에 대해 더 잘 알수록, ‘computationally efficient한’ 방법을 사용할 수 있을 가능성이 높다.
다만, ‘데이터에 대해 잘 알고 통계모델링에 대해서도 잘 아는 사람’이 흔치 않다는 것이 문제인데… 그래서 필자는 그 흔치 않은 사람 중 하나가 되고자 이 블로그를 운영하는 등의 노력을 지속할 계획이다.