건물의 시간별 전기부하 학습 후 예측하기 - 딥러닝 대신 회귀분석으로
시계열 데이터에 대해, 경우에 따라서는 전통적인 선형회귀가 딥러닝보다 시간을 훨씬 덜 쓰고도 더 좋은 예측력을 보인다는 놀라운(?) 사실을 아는가?
건물의 시간별 전기 부하
다음 그림은, 어떤 건물의 특정 1주일 간 각 시간별 전기 사용량 그래프들이다. 파란색 곡선은 K년도의 특정 1주일이고 (K는 2010~2022 사이의 어떤 자연수), 초록색 곡선은 K+1년도에서의 같은 1주일이다. (정확히는, K년도의 최대부하가 1000이 되도록 scaling한, 일종의 ‘가명처리’를 한 데이터이다)
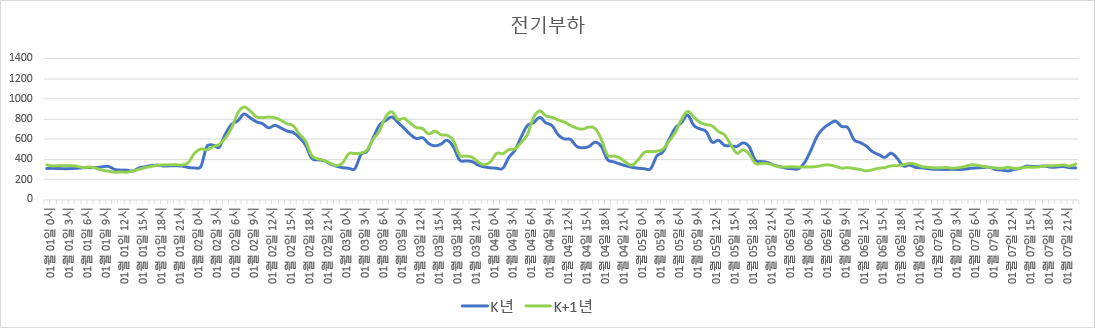
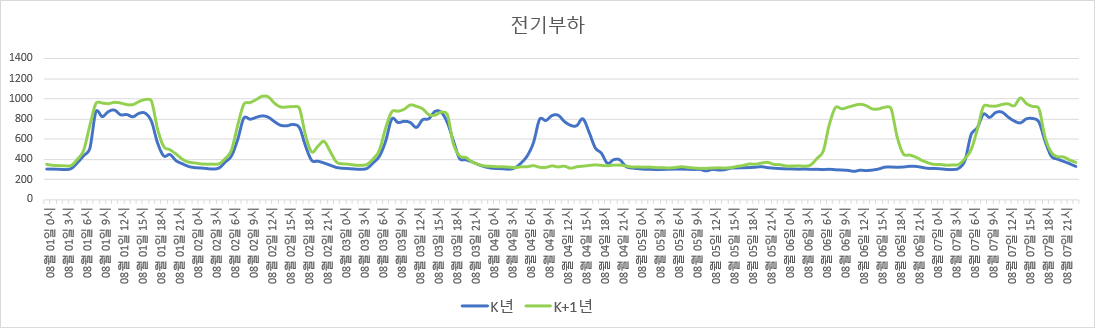
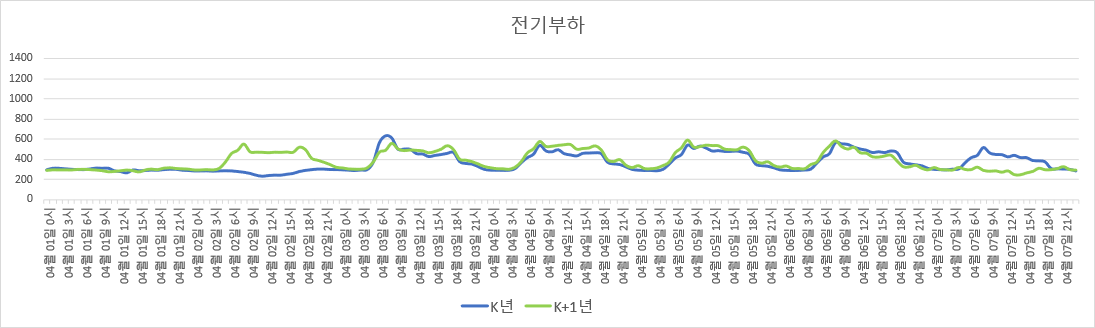 특정 건물 내 1주일 간의 시간별 전기 부하 (위에서부터 겨울, 여름, 봄)
특정 건물 내 1주일 간의 시간별 전기 부하 (위에서부터 겨울, 여름, 봄)
두 해의 전기 사용량 패턴의 높이나 전반적인 모양이 비슷하다 (위 그림에서 모양이 차이가 나는 부분은 평일/휴일 차이다). 그러므로 해당 건물의 사용 행태나 건물 규모 또는 전기 요금체계 등에 급격한 변화가 없다면, 매년 비슷한 전기 사용 패턴을 보이리라 추측된다.
그렇다면, K년도의 시간별 전기부하를 어떤 predictor들의 함수로써 학습시켰을 때, K+1년도의 predictor들 값만을 이용해 K+1년의 전기부하를 실제에 가깝게 예측할 수 있을까? 그리고 그 예측에는 어떤 방법을 사용해야 할까? 딥러닝 (Recurrent Neural Network 등)? 전통적인 선형회귀?
이러한 학습 및 예측을 수행해 보자. 이번 포스팅에서는, ‘딥러닝을 쓰지 않고’ 회귀분석으로 예측하는 모델을 구성해본다.
회귀모델 설명
Predictor로는 기온과 일조를 선택했다. ‘기상청에서 쉽게 구할 수 있으면서’ 건물의 에너지 사용량에 영향을 미칠 것으로 추정되기 때문이다. 기온은 건물의 냉난방 부하에 큰 영향을 미치고, 일조도 냉난방 부하에 어느 정도 영향을 미치면서 조명 부하에도 약간 영향을 미칠 것으로 추정된다. (기상청 종간기상관측자료 링크)
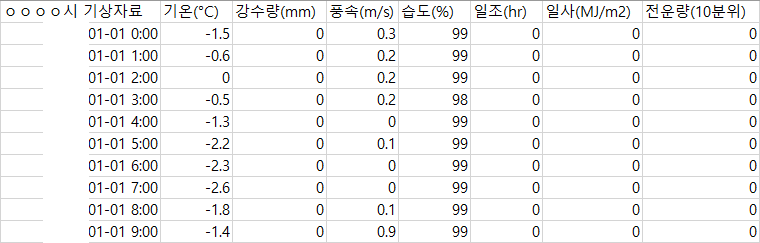 기상청 종간기상관측자료에서 다운로드받은, 시간별 기온과 일조 자료 예시.
기상청 종간기상관측자료에서 다운로드받은, 시간별 기온과 일조 자료 예시.
기온과 일조를 이용해 건물 전기 부하 예측이 높은 정확도로 가능하다면, 기상청에서 다음 날의 시간별 기온과 일조 예보를 보고 다음 날의 전기 부하 예측이 가능할 것이다.
우선 기온과 조도를 predictor로 추가한다.
그리고 시간별 dummy variable들과 월별 dummy variable들도 회귀모델의 predictor로 추가한다. 하루 24시간 내의 각 시간별로는 전기 사용량이 다르고, 그 24시간 동안의 전기 부하 패턴의 모양도 월별로 다를 수 있기 때문이다 (특히 냉방/난방용 전기 사용이 있는 계절의 경우).
그리고 기온의 영향 또한 시간 및 월에 따라 다를 수 있으므로, dummy variable들과 기온 및 조도 간 상호작용항들도 추가한다.
여기서 약간의 도메인 지식에 기반해 다시 생각해보면, 기온과 조도가 부하에 영향을 크게 미치는 기간은 냉방/난방 설비를 가동하는 하절기와 동절기의 평일일 것으로 추정된다. 바꿔 말하면, 냉방/난방 설비를 가동하지 않는 춘추절기 및 휴일에는 기온과 조도의 영향이 미미할 것으로 추정된다.
그리고 맨 위의 그림을 잘 보면, 같은 평일이라도 겨울의 평일, 여름의 평일, 봄/가을의 평일의 24시간 동안의 전기부하 패턴의 모양에는 서로 차이가 있다.
구체적으로, 난방기간의 경우 아침에 부하가 제일 높고 퇴근시간까지 완만하게 감소하지만, 냉방기간의 경우 아침의 부하가 퇴근시간까지도 별로 줄어들지 않는다. 한편 냉/난방 기간이 아닌 경우 부하 자체가 작은 편이다. 또한 휴일의 부하패턴 모양은 평일과 달리 평평하며, 대신 이러한 평평한 패턴은 모든 계절에 대해 비슷하다.
이러한 점들을 고려할 때, 모델을 아래의 4개 sub모델들로 분리하는 것이 적절해 보인다.
1) 냉방설비 가동기간 (5~9월) 평일 (Predictor는 월더미, 시간더미, 기온도, 일조, 월별 dummy와 시간별 dummy가 기온의 일차항 및 이차항과 곱해진 교차항들임)
2) 난방설비 가동기간 (11~3월) 평일 (Predictor는 하절기 평일 모델에서와 같음)
3) 그 외 기간 (4월, 10월) 평일 (Predictor는 시간별 dummy)
4) 휴일 (Predictor는 월별 dummy와 시간별 dummy)
K년도의 자료를 갖고, 위 4개 sub모델 중 1), 2)에 대해서는 Weighted Least Squares (WLS) 를 개별로 수행한다. Weight는 부하가 큰 시간일수록 크게 (즉 부하 값으로) 배정했다. 3), 4)에 대해서는 통상적인 Ordinary Least Squares (OLS) 를 개별로 수행했다.
Sub모델 1), 2)에 대해 WLS를 쓴 이유는, 모델이 냉/난방으로 인한 최대부하 값을 보다 더 잘 추정하도록 하기 위함이다 (최대부하 정보가 기본요금 설정 및 전력계통 설비 용량 선정 관점에서 중요한 정보이므로).
시간 $t$에서의 전기 부하를 $p_t$, 설명변수 벡터를 $x_t$라 할 때, 4개 sub모델 중 $j$번째 sub모델 $\mathcal{M}_{j}$의 계수 $\beta_j$에 대한 수식은 아래와 같다.
Minimize $ \sum_{t \in \mathcal{M}_{j}} w_{t} (p_{t} - x_{t}^{\top} \beta_j)^2 $
where $ w_{t} = p_{t}$ if $j \in \lbrace 1,2 \rbrace$, $w_{t} = 1 $ if $j \in \lbrace 3,4 \rbrace$
이는 $w_{t}$를 가중치로 하는 WLS이다. 위 목적함수를 최소화하는 $\beta_j$의 추정량 $\hat{\beta}_j$를 구한다. $\hat{\beta}_j$를 구하는 데에는 $K$년도의 자료만 사용하고, $K+1$년도의 자료는 사용하지 않음에 주의한다.
회귀모델 적합 결과
적합된 회귀모델에, K+1년도의 각 시간별 설명변수 값들을 대입하면 K+1년도의 시간별 전기부하 추정치를 $\hat{p}_t = x_{t}^{\top} \hat{\beta}_j$ 로 구할 수 있다. 물론 이는 실제 전기부하 $p_t$와는 다르지만, 모델이 잘 적합되었다면 매우 비슷할 것이다. 이 회귀모델의 적합도는 얼마나 될까?
Adjusted $R^2$를 계산해보면, 훈련 set (K년도)에 대해서는 0.9220, 검증 set (K+1년도)에 대해서는 0.8706이다. 그림으로 보이면 아래와 같다
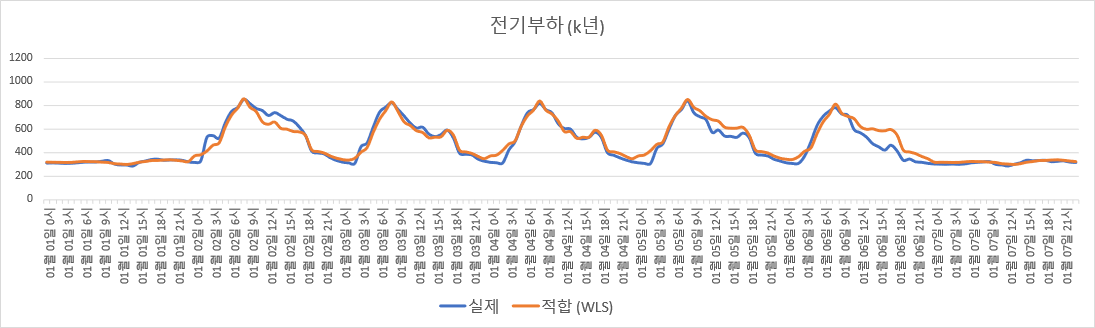
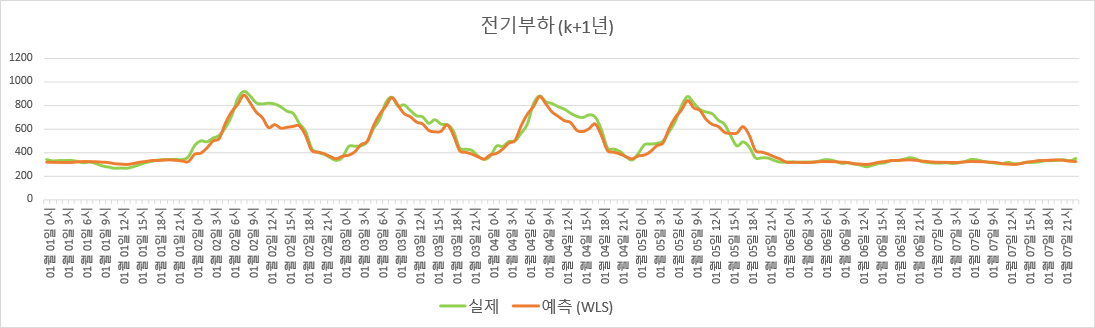 $K$년도 데이터로 적합한 회귀모델 기반 전기부하 추정.
$K$년도 데이터로 적합한 회귀모델 기반 전기부하 추정.
기상청의 공개 자료만을 사용했고 회귀모델 계산이 몇 초만에 된다는 걸 생각해보면, 구하기 쉬운 데이터와 적은 계산비용으로 나름 괜찮은 성능의 모델을 얻었다고 볼 수 있다.
오차의 자기상관을 Seasonal ARMA로 모델링
위 휘귀모델에는 사실 오차의 자기상관 (autocorrelation in disturbances) 문제가 남아있다. 위 그림들에서 실제값과 예측값을 잘 보면, 예측값이 실제값보다 큰 시간이 어느 정도 연속되다가, 반대로 예측값이 실제값보다 작은 시간이 어느 정도 연속되는 것이 반복된다.
실제로 각 sub모델별로 잔차에 대해 ACF (AutoCorrelation Function) 및 PACF (Partial ACF) plot을 그려보면, 아래 왼쪽 그림의 ACF plot에서 보듯 오차의 자기상관이 뚜렷하다. 시계열 데이터의 자기상관성 검정을 위한 Ljung-Box test 수행 시 $p$-value가 사실상 0으로 계산되어서, 자기상관이 없다는 귀무가설이 기각된다.
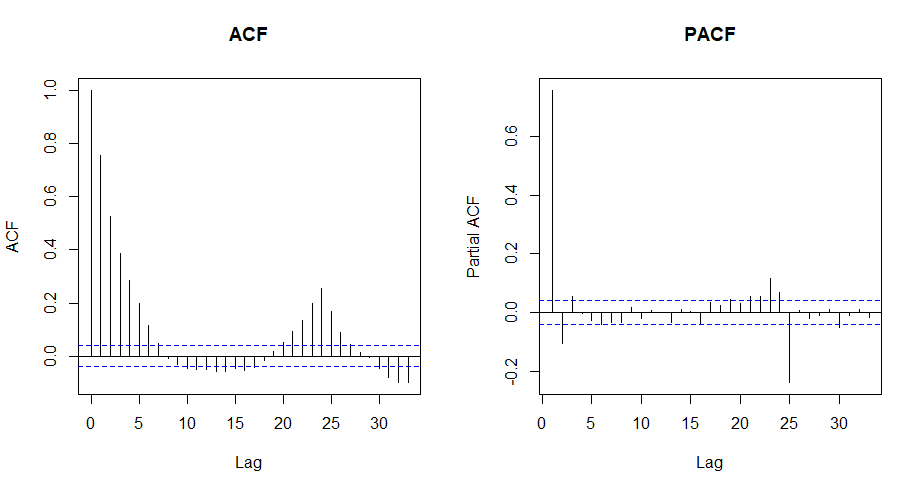 하절기 sub모델의 잔차에 대한 ACF와 PACF plot.
하절기 sub모델의 잔차에 대한 ACF와 PACF plot.
이는 아직 ‘주’회귀모델의 잔차로부터 얻을 수 있는 ‘자기상관’ 정보가 남아 있음을 의미한다. 그렇다면 각 sub모델별로 $K$년도의 잔차들에 대해 ARIMA 기반의 ‘보조’회귀모델을 적합하고, 해당 보조회귀모델로 $K+1$년도의 잔차들을 설명하면 최종 회귀모델의 성능 향상이 기대된다.
($K+1$년도의 실제 부하를 모르는데 $K+1$년도의 ‘잔차’를 사용하는 모델을 어떻게 쓰냐고 반문할 수 있다. 그러나 만약 현재가 $K+1$년도의 $q$번째 시점이라 하면, $q-1, q-2, \cdots$번째 시점의 ‘실제 부하’를 알게 되므로, $q-1, q-2, \cdots$ 시점들의 잔차가 계산된다. 그리고 위에서 언급했듯 잔차에 대한 ‘보조’회귀모델을 ARIMA 모델로 만들면, $q$번째 시점 이전의 잔차만을 설명변수로 사용한다. 그러므로 $K+1$년도에 대해서도 적용이 가능하다.)
아랫첨자 $k$와 $k+1$가 연도를 나타낸다고 하자. 그러면 $p_{t,k}$와 $p_{t,k+1}$은 시점 $t$의 각 연도별 실제 전기부하, $x_{t,k}$와 $x_{t,k+1}$은 시점 $t$의 각 연도별 설명변수 벡터이다. 그러면 $ \hat{\epsilon}_{t,k} = p_{t,k} - x_{t,k}^{\top} \hat{\beta}_j $ 은 $K$년도의 잔차, $ \hat{\epsilon}_{t,k+1} = p_{t,k+1} - x_{t,k+1}^{\top} \hat{\beta}_j$ 는 $K+1$년도의 잔차이다.
이 때 $\hat{\epsilon}_{t,k}$에 대해 ARMA 보조회귀모델을 적합시킨다 (통계처리용 언어 R에서 $\texttt{auto.arima()}$ 함수를 사용. 단, 차분은 하지 않으며 drift와 mean은 사용하지 않는다). 즉 어떤 ‘선형’함수 $\hat{f}$에 대해 아래와 같이 두는 것이다 ($v_{t,k}$는 ARMA 보조회귀의 오차항).
$\hat{\epsilon}_{t,k} = \hat{f}(\hat{\epsilon}_{t-1,k}, \hat{\epsilon}_{t-2,k}, \cdots, v_{t-1,k}, v_{t-2,k},\cdots) + v_{t,k}$
해당 ARMA 보조회귀모델의 잔차 $\hat{v}_{t,k}$에 대해 ACF 및 PACF plot을 아래와 같이 그려보면, 자기상관성이 ‘거의’ 사라졌으나, 아직 24시간 주기의 자기상관성은 남아있다.
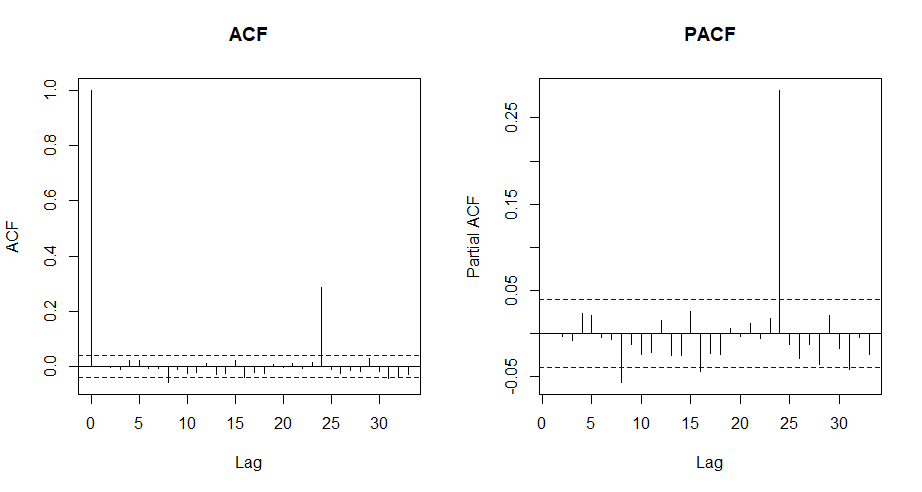 하절기 sub모델의 잔차에 대해 ARMA 모델을 적합시킨 후, ARMA 모델의 잔차에 대한 ACF와 PACF plot.
하절기 sub모델의 잔차에 대해 ARMA 모델을 적합시킨 후, ARMA 모델의 잔차에 대한 ACF와 PACF plot.
이는 전기 사용량 자체가 24시간 주기로 반복되는 특성이 있기 때문이다. Ljung-Box test를 수행 시 $p$-value 또한 lag 23까지에 대해서는 전부 0.1 이상이나 lag 24에 대해서는 사실상 0이므로, 24시간 주기의 자기상관성이 존재한다.
이는 seasonal ARMA (SARMA) 모델을 적합시켜 반영할 수 있다. 이를테면 $\texttt{auto.arima()}$로 적합된 모델이 ARIMA$(1,0,2)$라 하자. 그러면 $\texttt{Arima()}$ 함수를 사용해 SARIMA$(1,0,2)(1,0,1)_{24}$ 모델을 적합한다.
$\hat{\epsilon}_{t,k}$에 대해 SARMA 모델을 적합 후 해당 SARMA 모델의 잔차 $\hat{v}_{t,k}$에 대해 ACF 및 PACF plot을 아래와 같이 그려보면, 드디어 자기상관성이 완전히 사라졌다.
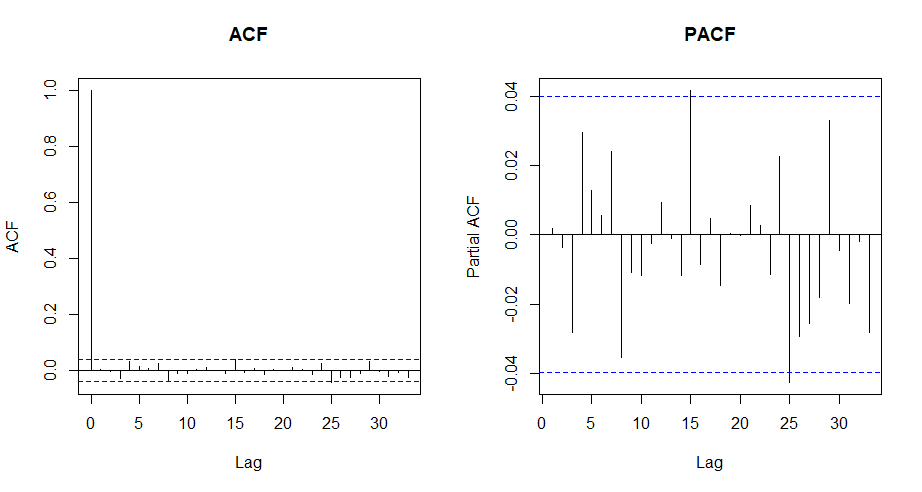 하절기 sub모델의 잔차에 대해 SARMA 모델을 적합시킨 후, SARMA 모델의 잔차에 대한 ACF와 PACF plot.
하절기 sub모델의 잔차에 대해 SARMA 모델을 적합시킨 후, SARMA 모델의 잔차에 대한 ACF와 PACF plot.
Ljung-Box test를 수행 시 $p$-value 또한 lag 24까지에 대해서도 0.1 이상이다. 또한 log-likelihood, AIC, BIC 등 지표도 ARMA 대비 SARMA 모델에서 더 좋았다.
$\hat{\epsilon}_{t,k}$에 대한 SARMA 적용 시 자기상관이 완전히 사라졌다는 것은, 기존 전기부하 자료에 강한 non-linearity가 존재하지 않음을 암시한다 (선형 모델로 거의 다 설명이 되니까).
일부 독자는 ‘회귀모델의 오차에 자기상관성 문제가 있으면, 시점 $t$의 전기 부하 예측 시의 설명변수로 과거 시점 ($t-1, t-2, \cdots$) 의 전기부하를 넣으면 되는 것 아닌가?’라고 생각할지도 모르겠다.
그러나 그 반대이다. 오차항에 자기상관이 있는 경우 과거 시점의 반응변수 (lagged dependent) 를 설명변수로 추가하면, 계수추정량이 ‘inconsistent’ 해진다는 것이 알려져 있다. Inconsistent란, ‘데이터가 많아져도 계수 추정량이 계수의 (숨겨진) 참값으로부터 벗어남’ 을 의미한다. (주로 계량경제 side의 회귀분석 강의에서 이를 가르친다)
오차의 자기상관 모델링을 통한 예측력 향상
$K$년도와 $K+1$년도 각각에 대해 SARMA 보조회귀모델의 맞춘값 $\hat{f}(\hat{\epsilon}_{t-1,k}, \cdots, \hat{v}_{t-1,k}, ,\cdots)$ 와 $\hat{f}(\hat{\epsilon}_{t-1,k+1}, \cdots, \hat{v}_{t-1,k+1}, ,\cdots)$ 를 얻는다.
(현실에서의 적용에서는, $K+1$년도인 경우 $t-1$ 시점까지의 실제 부하를 안다고 가정한다, 그래야 $\hat{\epsilon}_{t-1,k+1}, \hat{\epsilon}_{t-2,k+1}, \cdots$ 가 계산된다)
(그리고 $\hat{\epsilon}_{t,k+1}$으로 새로운 SARMA 보조회귀모델을 적합시킨 것이 아님에 유의. 만약 그랬다면 그건 반칙이다. $\hat{\beta}$와 $\hat{f}$는 어떤 경우에도 $K$년도 데이터만으로 추정되어야 한다.)
그러면, 아래처럼 주회귀모델의 맞춘값에 위 SARMA 보조회귀모델의 맞춘값을 더한 값이 최종적인 전기부하 추정량이다.
$\hat{p}_{t,k} = x_{t,k}^{\top} \hat{\beta}_j + \hat{f}(\hat{\epsilon}_{t-1,k}, \cdots, \hat{v}_{t-1,k}, ,\cdots)$
$\hat{p}_{t,k+1} = x_{t,k+1}^{\top} \hat{\beta}_j + \hat{f}(\hat{\epsilon}_{t-1,k+1}, \cdots, \hat{v}_{t-1,k+1}, ,\cdots)$
SARMA 보조회귀모델까지 사용해 추정하면, adjusted $R^2$가 증가할까?
그렇다. 훈련 set (K년도)에 대해서는 0.9220에서 0.9735으로, 검증 set (K+1년도)에 대해서는 0.8706에서 0.9725로 증가한다. 아래 그림을 보면, 오차의 자기상관을 반영하기 전과 비교해서, 예측값이 실제값에 더 가까워졌다.
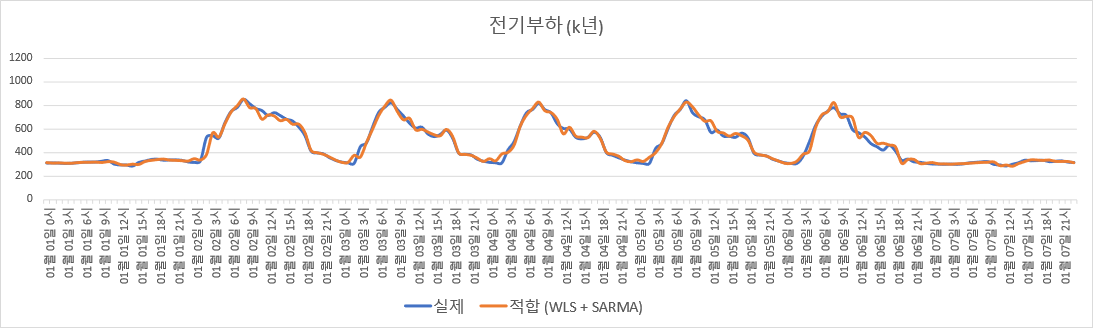
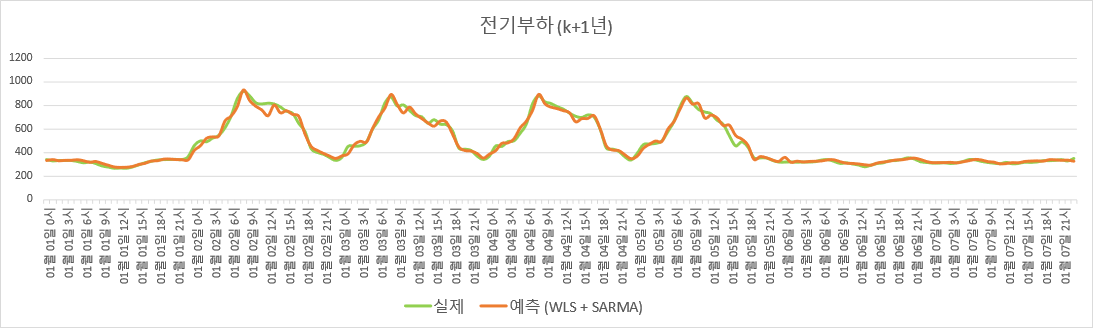 $K$년도 데이터로 적합한 주회귀모델 + 잔차 SARMA 모델 기반 전기부하 추정.
$K$년도 데이터로 적합한 주회귀모델 + 잔차 SARMA 모델 기반 전기부하 추정.
Adjusted $R^2$가 꼭 절대적인 기준은 아니겠지만, 딥러닝을 쓰지 않고 전통적 회귀분석 기법만을 사용해서 검증 set에 대해 Adjusted $R^2$ 0.95 이상을 달성한 것은 상당히 고무적이다.
R 코드
위 내용을 R로 구현한 코드는 아래와 같다. (GitHub Repo 링크)
rm(list = ls())
setwd(dirname(rstudioapi::getActiveDocumentContext()$path))
scriptpath <- getwd()
cat("\014")
library(forecast)
using.sarma.resids <- TRUE # If true, fit auxiliary SARMA models to the residuals of the main linear models
## load the dataset
## (the training case is a year (Jan. 1st ~ Dec. 31th), and the test case is the next year)
trainset.hourly <- read.table("trainset_hourly.txt") # data with 8760 rows (1st, 2nd, ..., 8760th hour for a year: each time step is an hour)
trainset.daily <- read.table("trainset_daytype.txt") # data with 365 rows (each time step is a day)
testset.hourly <- read.table("testset_hourly.txt")
testset.daily <- read.table("testset_daytype.txt")
actualpower.train <- trainset.hourly$V8 # actual power load in the building of each hour
actualpower.test <- testset.hourly$V8
temperature.train <- trainset.hourly$V1 # outdoor temperature of each hour
temperature.test <- testset.hourly$V1
daylight.train <- trainset.hourly$V5 # sunshine metric of each hour
daylight.test <- testset.hourly$V5
daytype.train <- rep(trainset.daily$V1,each=24) # 1 for working days, 0 for holidays
daytype.test <- rep(testset.daily$V1,each=24)
monthind.hourly <- rep(rep(c(1,2,3,4,5,6,7,8,9,10,11,12),c(31,28,31,30,31,30,31,31,30,31,30,31)),each=24) # corresponding month for each time step
hourind.hourly <- rep(c(1:24),365) # corresponding hour for each time step (1,2,...,23,24 is repeated 365 times)
itemindex <- rep(c(1:8760)) # neccesary for combining elements in the actual temporal order
dataset.train <- data.frame(actualpower.train, temperature.train, daylight.train, daytype.train, monthind.hourly, hourind.hourly,itemindex)
dataset.test <- data.frame(actualpower.test, temperature.test, daylight.test, daytype.test, monthind.hourly, hourind.hourly,itemindex)
names(dataset.train) <- c("power","temp","light","daytype","month","hour","itemindex")
names(dataset.test) <- c("power","temp","light","daytype","month","hour","itemindex")
## divide the dataset into four subperiods
dataset.train.holiday <- dataset.train[dataset.train$daytype==0,] # Holidays
dataset.train.workday <- dataset.train[dataset.train$daytype==1,] # Working days
dataset.train.springfall <- dataset.train.workday[dataset.train.workday$month %in% c(4,10),] # April, October
dataset.train.summer <- dataset.train.workday[dataset.train.workday$month %in% c(5,6,7,8,9),] # May ~ September
dataset.train.winter <- dataset.train.workday[dataset.train.workday$month %in% c(11,12,1,2,3),] # October ~ March
dataset.test.holiday <- dataset.test[dataset.test$daytype==0,]
dataset.test.workday <- dataset.test[dataset.test$daytype==1,]
dataset.test.springfall <- dataset.test.workday[dataset.test.workday$month %in% c(4,10),]
dataset.test.summer <- dataset.test.workday[dataset.test.workday$month %in% c(5,6,7,8,9),]
dataset.test.winter <- dataset.test.workday[dataset.test.workday$month %in% c(11,12,1,2,3),]
## using ONLY the training set (NOT the test set), fit the main linear model for each subperiod
## WLS for summer and winter (to correctly estimate peak power), OLS for spring/fall and holiday
model.train.springfall <- lm(power ~ factor(hour), data=dataset.train.springfall)
model.train.summer <- lm(power ~ temp*factor(month) + temp*factor(hour) + light*factor(month), data=dataset.train.summer, weight=power)
model.train.winter <- lm(power ~ temp*factor(month) + temp*factor(hour) + light*factor(month), data=dataset.train.winter, weight=power)
model.train.holiday <- lm(power ~ factor(month) + factor(hour), data=dataset.train.holiday)
## for the test set, compute predicted power and residuals using the main linear model fitted by the training set
predval.test.springfall <- data.frame(predict(model.train.springfall,dataset.test.springfall),dataset.test.springfall$itemindex)
predval.test.summer <- data.frame(predict(model.train.summer,dataset.test.summer),dataset.test.summer$itemindex)
predval.test.winter <- data.frame(predict(model.train.winter,dataset.test.winter),dataset.test.winter$itemindex)
predval.test.holiday <- data.frame(predict(model.train.holiday,dataset.test.holiday),dataset.test.holiday$itemindex)
resid.test.springfall <- dataset.test.springfall$power - predval.test.springfall[,1]
resid.test.summer <- dataset.test.summer$power - predval.test.summer[,1]
resid.test.winter <- dataset.test.winter$power - predval.test.winter[,1]
resid.test.holiday <- dataset.test.holiday$power - predval.test.holiday[,1]
## using ONLY the training residuals of the main linear models, fit the auxiliary SARMA models
## (do NOT use test residuals of the main linear models for fitting the auxiliary SARMA models)
## then, obtain the fitted values of auxiliary SARMA models for training and test residuals of the main linear models
if(using.sarma.resids){
Box.test(model.train.springfall$residuals,lag=24,type="Ljung",fitdf=0) # p-value near 0, indicating autocorrelation
autoarima.springfall <- auto.arima(model.train.springfall$residuals, max.d=0, allowdrift=FALSE, allowmean=FALSE)
sarma.springfall <- Arima(model.train.springfall$residuals,
order = c(autoarima.springfall$arma[1],0,autoarima.springfall$arma[2]),
seasonal= list(order = c(1,0,1), period=24), include.mean=FALSE)
Box.test(sarma.springfall$residuals,lag=24,type="Ljung",fitdf=0) # p-value should be over 0.1
auxfitval.train.springfall <- sarma.springfall$fitted
auxfitval.test.springfall <- Arima(resid.test.springfall, model=sarma.springfall)$fitted
Box.test(model.train.summer$residuals,lag=24,type="Ljung",fitdf=0)
autoarima.summer <- auto.arima(model.train.summer$residuals, max.d=0, allowdrift=FALSE, allowmean=FALSE)
sarma.summer <- Arima(model.train.summer$residuals,
order = c(autoarima.summer$arma[1],0,autoarima.summer$arma[2]),
seasonal= list(order = c(1,0,1), period=24), include.mean=FALSE)
Box.test(sarma.summer$residuals,lag=24,type="Ljung",fitdf=0)
auxfitval.train.summer <- sarma.summer$fitted
auxfitval.test.summer <- Arima(resid.test.summer, model=sarma.summer)$fitted
Box.test(model.train.winter$residuals,lag=24,type="Ljung",fitdf=0)
autoarima.winter <- auto.arima(model.train.winter$residuals, max.d=0, allowdrift=FALSE, allowmean=FALSE)
sarma.winter <- Arima(model.train.winter$residuals,
order = c(autoarima.winter$arma[1],0,autoarima.winter$arma[2]),
seasonal= list(order = c(1,0,1), period=24), include.mean=FALSE)
Box.test(sarma.winter$residuals,lag=24,type="Ljung",fitdf=0)
auxfitval.train.winter <- sarma.winter$fitted
auxfitval.test.winter <- Arima(resid.test.winter, model=sarma.winter)$fitted
Box.test(model.train.holiday$residuals,lag=24,type="Ljung",fitdf=0)
autoarima.holiday <- auto.arima(model.train.holiday$residuals, max.d=0, allowdrift=FALSE, allowmean=FALSE)
sarma.holiday <- Arima(model.train.holiday$residuals,
order = c(autoarima.holiday$arma[1],0,autoarima.holiday$arma[2]),
seasonal= list(order = c(1,0,1), period=24), include.mean=FALSE)
Box.test(sarma.holiday$residuals,lag=24,type="Ljung",fitdf=0)
auxfitval.train.holiday <- sarma.holiday$fitted
auxfitval.test.holiday <- Arima(resid.test.holiday, model=sarma.holiday)$fitted
## add the fitted values of auxiliary model to the fitted values of the main linear model
fitval.train.springfall <- data.frame(model.train.springfall$fitted.values +auxfitval.train.springfall,
dataset.train.springfall$itemindex)
fitval.train.summer <- data.frame(model.train.summer$fitted.values +auxfitval.train.summer,
dataset.train.summer$itemindex)
fitval.train.winter <- data.frame(model.train.winter$fitted.values +auxfitval.train.winter,
dataset.train.winter$itemindex)
fitval.train.holiday <- data.frame(model.train.holiday$fitted.values +auxfitval.train.holiday,
dataset.train.holiday$itemindex)
predval.test.springfall[,1] <- predval.test.springfall[,1] + auxfitval.test.springfall
predval.test.summer[,1] <- predval.test.summer[,1] + auxfitval.test.summer
predval.test.winter[,1] <- predval.test.winter[,1] + auxfitval.test.winter
predval.test.holiday[,1] <- predval.test.holiday[,1] + auxfitval.test.holiday
## when using.sarma.resids == FALSE, ignore the auxiliary SARMA model
} else {
fitval.train.springfall <- data.frame(model.train.springfall$fitted.values,
dataset.train.springfall$itemindex)
fitval.train.summer <- data.frame(model.train.summer$fitted.values,
dataset.train.summer$itemindex)
fitval.train.winter <- data.frame(model.train.winter$fitted.values,
dataset.train.winter$itemindex)
fitval.train.holiday <- data.frame(model.train.holiday$fitted.values,
dataset.train.holiday$itemindex)
}
## combine the values in the actual temporal order
fittedpower.train <- rep(0,8760)
for(i in 1:nrow(fitval.train.springfall)){
fittedpower.train[fitval.train.springfall[i,2]] = fitval.train.springfall[i,1]
}
for(i in 1:nrow(fitval.train.summer)){
fittedpower.train[fitval.train.summer[i,2]] = fitval.train.summer[i,1]
}
for(i in 1:nrow(fitval.train.winter)){
fittedpower.train[fitval.train.winter[i,2]] = fitval.train.winter[i,1]
}
for(i in 1:nrow(fitval.train.holiday)){
fittedpower.train[fitval.train.holiday[i,2]] = fitval.train.holiday[i,1]
}
predictedpower.test <- rep(0,8760)
for(i in 1:nrow(predval.test.springfall)){
predictedpower.test[predval.test.springfall[i,2]] = predval.test.springfall[i,1]
}
for(i in 1:nrow(predval.test.summer)){
predictedpower.test[predval.test.summer[i,2]] = predval.test.summer[i,1]
}
for(i in 1:nrow(predval.test.winter)){
predictedpower.test[predval.test.winter[i,2]] = predval.test.winter[i,1]
}
for(i in 1:nrow(predval.test.holiday)){
predictedpower.test[predval.test.holiday[i,2]] = predval.test.holiday[i,1]
}
## check whether the model is build well, based on adjusted R^2
adjrsq <- function(actual,estimate,k){
n <- length(actual)
sst <- sum((actual-mean(actual))^2)
ssr <- sum((actual-estimate)^2)
return(1 - (ssr/(n-k-1))/(sst/(n-k)) )
}
adjrsq.train <- adjrsq(actualpower.train,fittedpower.train,86)
adjrsq.test <- adjrsq(actualpower.test,predictedpower.test,86)
adjrsq.train
adjrsq.test # should be high enough
## Export the hourly fitted values (training set) and predicted power (test set)
write.table(fittedpower.train, "power_train_fit.txt",row.names=FALSE,col.names=FALSE)
write.table(predictedpower.test, "power_test_predict.txt",row.names=FALSE,col.names=FALSE)
그렇다면 딥러닝을 쓴다면 어떨까? Adjusted $R^2$ 0.99 정도는 쉽게 얻을 수 있을까?
이는 다음 포스팅에서 확인해 본다.