Logistic regression에서는 각 point 별로 response $y$가 0과 1 중 1일 확률 추정값 $\hat{y}$를 제공한다 (물론 실제 $y$값들은 알려져 있다). 한편, feature space에서 response가 1인 point들과 0인 point들이 완전히 linearly separable하면 (즉 $\hat{y}=0.5$를 기준으로 misclassified point가 하나도 없으면), logistic regression 추정이 되지 않음이 잘 알려져 있다.

Over-confidence란

Feature space에서 response가 1인 point들과 0인 point들이 ‘거의’ linearly separable인 경우 (즉 $\hat{y}=0.5$를 기준으로 misclassified point들이 ‘거의’ 없는 경우) 에도 문제가 발생한다. 이 경우 계수추정량들의 magnitude가 매우 커지고, 그 결과 추정값들이 모든 경우에 대해 1 또는 0에 아주 가까워진다. 이를 어느 class에 속할지에 대해 지나치게 확신한다고 해서, over-confidence라 한다.

Toy problem을 예시로 들면, 아래와 같은 두 class의 point들을 분류하는 plane을 ($\hat{y}=0.5$를 기준으로) logistic regression으로 찾는다고 하자.

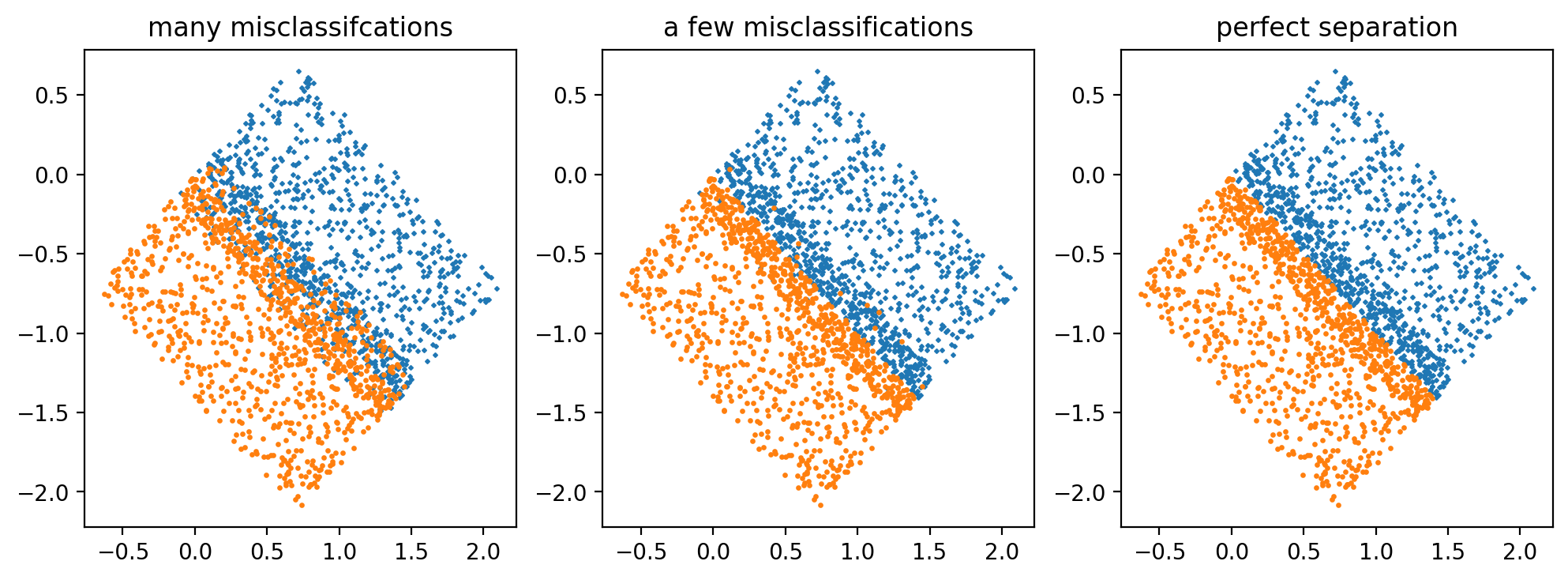overconfidence 두 class의 point들을 분류하는 plane을 찾는 문제, 각 경우에 대해 misclassified point 개수가 다름.

Plane을 $\beta_1 x_1 + \beta_2 x_2 + \beta_0 = 0$ 이라 할 때, 기울기가 -1이고 원점을 지나는 직선일 것이므로 $\beta_1 \approx \beta_2$,$\beta_0 \approx 0$임은 자명하다. 각 경우에 대해 $\beta_1$의 계수추정량들 및 계수추정량의 $t$-value들을 구하면 아래와 같다.

1) Many misclassifications: $\hat{\beta_1} = 8.85$, $t$-value는 $18.4$

2) A few misclassifications: $\hat{\beta_1} = 29.6$, $t$-value는 $13.8$

3) Perfect separation: $\hat{\beta_1} = 9,824$, $t$-value는 $0.8$

Misclassified point의 비중이 적을수록 계수추정량의 magnitude는 커지고, $t$-value는 작아진다. Python에서는 perfectly separable case에 대해서도 결과를 제공하기는 하는데, t-value를 보면 계수의 값에 별 의미는 없는 것으로 보인다.


Over-confidence가 발생하는 이유

Over-confidence에 대해 아주 엄밀한 설명은 아직 만나보지 못했지만, 필자가 간단히 수학적으로/ 직관적으로 생각해 본 바는 아래와 같다.

먼저 수학적으로는 다음과 같다.

로지스틱 회귀에서의 cost function은 ‘negative’ log-likelihood $-\sum_{i=1}^{N}[y_{i} \text{log}\hat{y}_{i} + (1-y_{i})\text{log}(1-\hat{y}_{i})]$ 이고 $ y_{i} \in \lbrace 0,1 \rbrace$이며 $0 \leq \hat{y}_{i}\leq 1$이다.

그러므로 실제 response가 1인 점을 기준으로, 추정값이 1에서 멀어지고 0으로 가까워질수록 penalty가 exponential하게 증가한다. 이는 실제 response가 0인데 추정값이 1에 가까워질 경우에도 마찬가지이다.

이 때 $\hat{y}=0.5$ 기준으로 misclassified point가 여럿 있는 경우에는, 해당 point들 때문에 생기는 exponential penalty를 줄이기 위해 추정값들이 1 또는 0에 너무 가까워지지 않도록 계수의 magnitude를 작게 설정해야 한다.

그러나 계수의 magnitude를 작게 할수록, 실제 값이 1이고 추정값이 1에 가까운 경우에도 완전히 1에 매우 가깝기보다는 1보다 어느 정도는 작은 값이 될 것이다. 실제 값이 0이고 추정값이 0인 경우에도 0보다 어느 정도는 큰 값이 될 것이다. 이 차이 또한 작게나마 penalty로 계산된다.

misclassified point가 매우 조금밖에 없을 경우에는, misclassified point의 penalty가 아무리 exponential하게 증가한다고 해도 그 숫자 자체가 매우 적기 때문에, 올바르게 분류된 point들에 대한 $\hat{y}$가 1 또는 0에 매우 가까워지도록 계수의 magnitude를 크게 설정하는 것이 total penalty를 더 작게 만드는 선택일 수 있는 것이다.


다음으로 직관적으로는 아래와 같다.

Misclassified point가 여럿 있는 경우에는, boundary 근처 point들에 대해 이 분류가 맞다는 확신을 가지기가 어려울 것이다 (말 그대로 misclassification이 많으니까). 그래서 확률 추정값을 0.5에 가깝게 주는 것이 자연스럽다.

그러나 misclassified point가 거의 없는 경우에는, 분류가 잘 되니 boundary 근처 point들에 대해서도 보다 더 확신을 가질 것이다. 그러므로 확률 추정값도 0 또는 1에 가깝게 준다고 보는 것이 자연스럽다.