Beer-Quiche game (동태적 미비정보 게임) 답안
아래 링크의 글을 보면, 자율주행차 구현을 위해서는 앞 차의 type을 고려한 Dynamic Bayesian update로 ‘equilibrium’ 을 계산하는 게임이론 방법론이 필요하다고 한다.
관련 예시로 Beer-Quiche game을 들었는데, 해당 예시에 대해 필자 나름의 답안을 작성해보았다.
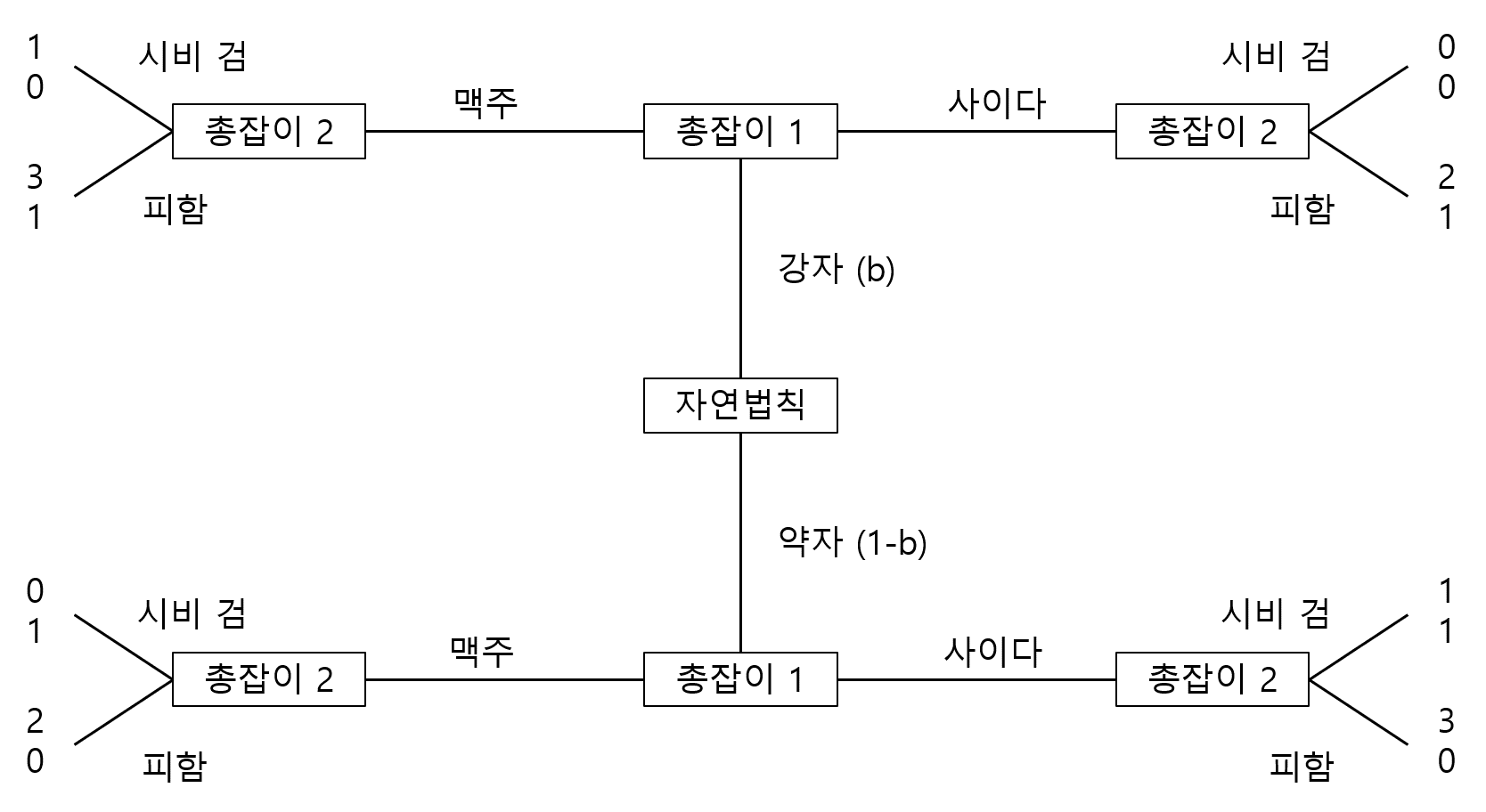
게임 구성
서부개척시대의 술집에 총잡이 두 명이 있다. 총잡이 1은 마실 것을 찾으러 왔으며, 총잡이 2는 총잡이 1에게 시비를 걸고 싸워서 돈을 뜯어내는 시도를 할 지 고민 중이다. 총잡이 1은 총잡이 2가 자신에게 시비를 걸 지 말지 고민한다는 것을 알고 있다.
총잡이 1은 강자(strong)이거나 약자(weak), 두 가지 유형 중 하나다. 총잡이 1이 강자라면, 총잡이 2는 시비를 걸더라도 돈을 뜯지 못하고, 결국 총잡이 2는 0의 보수를 얻는다. 오히려 강자인 총잡이 1에게 시비를 안 걸고 피할 경우, 총잡이 2는 1의 보수를 얻는다. 반면 총잡이 1이 약자라면, 총잡이 2는 시비를 걸어서 돈을 뜯을 수 있고 그 결과 총잡이 2는 1의 보수를 얻는다. 만약 총잡이 1이 약자인데 총잡이 2가 시비를 안 걸고 피하면, 총잡이 2는 0의 보수를 얻는다.
총잡이 1은 기본적으로 싸움을 좋아하지 않는다. 따라서 자신의 유형 (강자인지 약자인지) 에 상관없이 총잡이 2가 자신에게 시비를 걸지 않으면 기본적으로 2의 보수를 얻고, 시비를 걸어오면 기본적으로 0의 보수를 얻는다.
총잡이 1은 자신의 유형을 알지만, 총잡이 2는 총잡이 1의 유형을 정확히는 모른다. 다만 총잡이 2는 총잡이 1이 강자일 확률이 $b$라고 믿고 있다 ($0<b<1$). $b$의 값은 총잡이 2 뿐 아니라 총잡이 1도 알고 있는, 즉 모두가 알고 있는 사실 (주지사실) 이다.
이 세계에선 일반적으로 강자들은 맥주를 좋아하고, 약자들은 사이다를 좋아한다. 총잡이 1은 맥주 또는 사이다를 마시는데, 자신의 유형에 맞게 좋아하는 음료를 마시면 (강자일 경우 맥주, 약자일 경우 사이다) 위에서 설명한 상황 별 보수에 더해 추가로 1의 보수를 얻는다. 좋아하지 않는 음료를 마시면 추가 보수는 0이다.
총잡이 2는 총잡이 1이 뭘 마시는지 ‘본 뒤에’ 총잡이 1에게 시비를 걸 지 말지 결정한다. 즉 일반적인 선호도에 근거해 총잡이 1이 맥주를 시키면 피하고 사이다를 시키면 시비를 걸 수도 있지만, 총잡이 1이 맥주를 시키는 것을 ‘약자인데 강자인 척하는 것’ 으로 보고 시비를 걸 수도 있다. 총잡이 1과 2는 모두 합리적이며 상황 별 보수들이 주지사실이므로, 게임이론에 따라 행동을 결정한다.
가정 A: 총잡이 1이 강하면 맥주, 약하면 사이다를 마신다고 가정 시
가정 A 하에서 총잡이 2는 총잡이 1이 뭘 마시는지 보고 총잡이 1의 유형을 특정할 수 있다. 총잡이 1이 맥주를 마신다면 강자로 생각되므로, 총잡이 2는 시비를 걸지 말아야 한다 (시비 걸면 0, 안 걸면 1이므로). 총잡이 1이 사이다를 마신다면 약자로 생각되므로, 총잡이 2는 시비를 걸어야 한다 (시비 걸면 1, 안 걸면 0이므로).
총잡이 1은 총잡이 2의 위와 같은 생각을 합리적으로 예상할 수 있다. 따라서 총잡이 2가 맥주를 보면 자신을 피하고 사이다를 보면 덤빈다는 걸 염두에 두고 나서 뭘 마실 지 결정한다고 하자.
이 때 총잡이 1 자신이 강자라면, 가정 A대로 맥주를 마시는 게 좋다. 어차피 맥주를 본 총잡이 2가 자신을 피할 것이므로 총 3의 보수를 얻으며 (싸움 회피 2 + 선호하는 음료 1), 이는 괜히 사이다로 바꿔서 얻는 보수 0보다 크기 때문이다 (시비 걸림 0 + 선호하지 않는 음료 0).
그러나 총잡이 1 자신이 약자라면, 가정 A대로 사이다를 마시는 것 보다는 맥주로 음료를 ‘바꾸는’ 게 좋다. 사이다를 마시면 1의 보수를 얻지만 (시비 걸림 0 + 선호하는 음료 1), 맥주를 마시면 2의 보수를 얻기 때문이다 (싸움 회피 2 + 선호하지 않는 음료 0).
따라서 가정 A (강자면 맥주, 약자면 사이다) 하에서 총잡이 2가 할 행동 (맥주 보면 피하고, 사이다 보면 덤비기) 을 전제로 한 총잡이 1의 최선의 행동 (강자든 약자든 맥주) 이 가정 A와 같지 않으므로, 가정 A 하에서는 완전베이즈균형이 성립하지 않는다.
가정 B: 총잡이 1이 강하든 약하든 맥주를 마신다고 가정 시
가정 B 하에서는 총잡이 2가 총잡이 1의 음료를 보더라도 총잡이 1이 강자인지 약자인지 특정할 수 없다 (둘 다 똑같이 맥주이므로). 따라서 총잡이 1이 $b$의 확률로 강자, $1-b$의 확률로 약자라고 생각하고 기대보수를 계산해 본다.
총잡이 2가 시비를 걸 때 총잡이 1이 강자였다면 총잡이 2는 0의 보수를, 약자였다면 1의 보수를 얻는다. 그러므로 총잡이 1에게 시비를 걸 경우 기대보수는 $1-b$이고 ($0 \times b + 1 \times (1-b)$), 시비를 걸지 않을 경우 기대보수는 b이다 ($ 1 \times b + 0 \times (1-b)$).
[가정 2를 따르고 $b>0.5$ 인 (총잡이 1이 강자일 확률이 더 높은) 경우]
이 때 총잡이 2의 기대보수는 시비를 걸지 않을 때 더 높으므로 총잡이 2는 싸움을 포기한다. 총잡이 1은 총잡이 2의 이러한 생각을 합리적으로 예상할 수 있다. 따라서 총잡이 2가 맥주를 보면 피한다는 걸 염두에 두고 뭘 마실 지 결정한다.
총잡이 1 자신이 강자라면, 가정 B대로 맥주를 마시는 게 좋다. 어차피 맥주를 본 총잡이 2가 자신을 피할 것이므로 총 3의 보수를 얻으며, 이는 괜히 사이다로 바꿔서 얻는 보수 (총잡이 2가 사이다를 보고 시비를 건다면 0, 시비를 걸지 않더라도 선호하는 음료가 아니므로 2) 보다 크기 때문이다.
총잡이 1 자신이 약자라면, ‘가정 B 하에서 그러지는 않겠지만 만약 자신이 맥주 대신 사이다를 마신다면 총잡이 2가 어쩔 것인가’ 에 따라 맥주와 사이다 중 무엇이 더 나은 선택인지가 결정된다.
만약 총잡이 2가 사이다를 보고 시비를 건다면, 총잡이 1은 가정 B대로 맥주를 마시는 게 좋다. 맥주를 좋아하지는 않지만 싸움을 피하므로 2의 보수를 얻는데, 이는 사이다를 마시지만 시비를 걸려서 얻는 보수 1보다 크기 때문이다. 그러나 총잡이 2가 사이다를 보고도 시비를 걸지 않는다면, 총잡이 1은 가정 B와 달리 음료를 사이다로 바꾸는 게 좋다. 시비도 안 걸리는데 좋아하는 음료까지 마시므로 3의 보수를 얻고, 이는 맥주를 마셔서 얻는 보수 2보다 크기 때문이다.
따라서 가정 B (강자든 약자든 맥주) 하에서 $b>0.5$ (강자일 확률이 더 높음) 인 경우 총잡이 2가 할 행동 (맥주를 보고 피함) 을 전제로 한 총잡이 1의 최선의 행동은 ‘총잡이 2가 사이다를 보면 시비를 건다’ 라는 추가 가정 하에 가정 B와 일치한다. 따라서 가정 2 및 $b>0.5$ 조건 하에서는 총잡이 2가 사이다를 보고 덤빈다는 추가 가정 하에 완전베이즈균형이 성립한다.
이 때 총잡이 2가 사이다를 보고 덤빈다는 것은, 사이다를 보고 총잡이 1이 약자라고 판단한다는 뜻이기도 하다. 시비를 걸 때의 기대보수가 더 높아야 시비를 걸 텐데, 약자를 상대로 시비를 걸어야 총잡이 2가 보수를 얻기 때문이다. 이게 타당하려면, ‘총잡이 2가 반드시 시비를 건다고 할 때’ 총잡이 1이 실제로 약자인 경우 사이다를 맥주보다 선호해야 한다. 그리고 이는 사실이다, 어차피 시비는 걸린다면 자신이 좋아하는 사이다를 마실 때 1의 보수를 얻는 반면 맥주를 먹으면 0의 보수를 얻기 때문이다. 그러므로 총잡이 2의 신념체계는 직관적으로도 옳다.
[가정 B를 따르고 $b<0.5$ 인 (총잡이 1이 약자일 확률이 더 높은) 경우]
이 때 총잡이 2의 기대보수는 시비를 걸 때 더 높으므로 총잡이 2는 시비를 건다. 총잡이 1은 총잡이 2의 이러한 생각을 합리적으로 예상할 수 있다. 따라서 총잡이 2가 맥주를 보면 시비를 건다는 걸 염두에 두고 뭘 마실 지 결정한다.
이 경우 ‘가정 B 하에서 그러지는 않겠지만 만약 자신이 맥주 대신 사이다를 마신다면 총잡이 2가 어쩔 것인가’ 에 따라 맥주와 사이다 중 무엇이 더 나은 선택인지가 결정된다.
만약 총잡이 2가 사이다를 보고 시비를 건다면, 총잡이 1은 자신이 강할 경우 가정 B대로 맥주를 마시는 게 좋다. 어차피 뭘 해도 시비를 걸리는데, 좋아하는 맥주라도 마시는 것이 보수가 더 높기 때문이다 (맥주 마시면 1, 사이다 마시면 0). 그러나 자신이 약할 경우 ‘가정과 달리’ 사이다를 마시는 게 좋다. 어차피 시비를 걸린다면 좋아하는 사이다를 마시는 것이 보수가 더 높기 때문이다 (맥주 마시면 0, 사이다 마시면 1).
만약 총잡이 2가 사이다를 보고 피한다면, 총잡이 1은 자신이 강할 경우 ‘가정 B와 달리’ 맥주 대신 사이다를 마시는 게 좋다. 좋아하는 맥주는 못 마시지만 싸움을 피할 수 있기 때문이다 (맥주 마시고 시비 걸리면 1, 사이다 마시고 싸움 피하면 2). 한편 총잡이 1 자신이 약할 경우에도 맥주 대신 사이다를 마시는 게 좋다. 좋아하는 사이다도 마시고 싸움도 피할 수 있기 때문이다 (맥주 마시고 시비 걸리면 0, 사이다 마시고 싸움 피하면 3).
따라서 가정 B (강자든 약자든 맥주) 하에서 $b<0.5$ (약자일 확률이 더 높음) 인 경우 총잡이 2가 할 행동 (맥주를 보고 시비 검) 을 전제로 한 총잡이 1의 최선의 행동은 어떤 경우에도 가정 B와 같지 않다. 따라서 가정 B 및 $b<0.5$ 조건 하에서는 완전베이즈균형이 성립하지 않는다.
가정 C: 총잡이 1이 강하면 사이다, 약하면 맥주를 마신다고 가정 시
가정 C 하에서 총잡이 2는 총잡이 1이 뭘 마시는지 보고 총잡이 1의 유형을 특정할 수 있다. 총잡이 1이 맥주를 마신다면 약자로 생각되므로, 총잡이 2는 시비를 걸어야 한다 (시비 걸면 0, 안 걸면 1이므로). 총잡이 1이 사이다를 마신다면 강자로 생각되므로, 총잡이 2는 시비를 걸지 말아야 한다 (시비 걸면 0, 안 걸면 1이므로).
총잡이 1은 총잡이 2의 위와 같은 생각을 합리적으로 예상할 수 있다. 따라서 총잡이 2가 맥주를 보면 자신에게 덤비고 사이다를 보면 피한다는 걸 염두에 두고 나서 뭘 마실 지 결정한다고 하자.
이 때 총잡이 1 자신이 강자라면, 가정 C대로 사이다를 마시는 게 좋다. 좋아하는 맥주를 마시지는 못하지만 싸움을 피해서 얻는 보수 2가, 맥주를 마시지만 시비를 걸려서 얻는 보수 1보다 크기 때문이다.
그러나 총잡이 1 자신이 약자라면, 가정 C와 달리 사이다로 음료를 ‘바꾸는’ 게 좋다. 맥주를 마시면 0의 보수를 얻지만 (시비 걸림 0 + 선호하지 않는 음료 0), 사이다를 마시면 3의 보수를 얻기 때문이다 (싸움 회피 2 + 선호하는 음료 1).
따라서 가정 C (강자면 사이다, 약자면 맥주) 하에서 총잡이 2가 할 행동 (맥주 보면 덤비고, 사이다 보면 피하기) 을 전제로 한 총잡이 1의 최선의 행동 (강자든 약자든 사이다) 이 가정 C와 같지 않으므로, 가정 C 하에서는 완전베이즈균형이 성립하지 않는다.
가정 D: 총잡이 1이 강하든 약하든 사이다를 마신다고 가정 시
가정 D 하에서는 총잡이 2가 총잡이 1의 음료를 보더라도 총잡이 1이 강자인지 약자인지 특정할 수 없다 (둘 다 똑같이 사이다이므로). 따라서 총잡이 1이 $b$의 확률로 강자, $1-b$의 확률로 약자라고 생각하고 기대보수를 계산해 본다.
총잡이 2가 시비를 걸 때 총잡이 1이 강자였다면 총잡이 2는 0의 보수를, 약자였다면 1의 보수를 얻는다. 그러므로 총잡이 1에게 시비를 걸 경우 기대보수는 $1-b$이고 ($0 \times b + 1 \times (1-b)$), 시비를 걸지 않을 경우 기대보수는 $b$이다 ($1 \times b + 0 \times (1-b)$).
[가정 D를 따르고 $b>0.5$ 인 (총잡이 1이 강자일 확률이 더 높은) 경우]
이 때 총잡이 2의 기대보수는 시비를 걸지 않을 때 더 높으므로 총잡이 2는 싸움을 포기한다. 총잡이 1은 총잡이 2의 이러한 생각을 합리적으로 예상할 수 있다. 따라서 총잡이 2가 사이다를 보면 피한다는 걸 염두에 두고 뭘 마실 지 결정한다.
총잡이 1 자신이 약자라면, 가정 D대로 사이다를 마시는 게 좋다. 어차피 사이다를 본 총잡이 2가 자신을 피할 것이므로 총 3의 보수를 얻으며, 이는 괜히 맥주로 바꿔서 얻는 보수 (총잡이 2가 맥주를 보고 시비를 건다면 0, 시비를 걸지 않더라도 선호하는 음료가 아니므로 2) 보다 크기 때문이다.
총잡이 1 자신이 강자라면, ‘가정 D 하에서 그러지는 않겠지만 만약 자신이 사이다 대신 맥주를 마신다면 총잡이 2가 어쩔 것인가’ 에 따라 맥주와 사이다 중 무엇이 더 나은 선택인지가 결정된다.
만약 총잡이 2가 맥주를 보고 시비를 건다면, 총잡이 1은 가정 D대로 사이다를 마시는 게 좋다. 사이다를 좋아하지는 않지만 싸움을 피하므로 2의 보수를 얻는데, 이는 맥주를 마시지만 시비를 걸려서 얻는 보수 1보다 크기 때문이다. 그러나 총잡이 2가 맥주를 보고도 시비를 걸지 않는다면, 총잡이 1은 가정 D와 달리 음료를 맥주로 바꾸는 게 좋다. 시비도 안 걸리는데 좋아하는 음료까지 마시므로 3의 보수를 얻고, 이는 사이다를 마셔서 얻는 보수 2보다 크기 때문이다.
따라서 가정 D (강자든 약자든 사이다) 하에서 $b>0.5$ (강자일 확률이 더 높음) 인 경우 총잡이 2가 할 행동 (사이다를 보고 피함) 을 전제로 한 총잡이 1의 최선의 행동은 ‘총잡이 2가 맥주를 보면 시비를 건다’ 라는 추가 가정 하에 가정 D와 일치한다. 따라서 가정 D 및 $b>0.5$ 조건 하에서는 총잡이 2가 맥주를 보고 덤빈다는 추가 가정 하에 완전베이즈균형이 성립한다.
이 때 총잡이 2가 맥주를 보고 덤빈다는 것은, 맥주를 보고 총잡이 1이 약자라고 판단한다는 뜻이기도 하다. 시비를 걸 때의 기대보수가 더 높아야 시비를 걸 텐데, 약자를 상대로 시비를 걸어야 총잡이 2가 보수를 얻기 때문이다. 이게 타당하려면, ‘총잡이 2가 반드시 시비를 건다고 할 때’ 총잡이 1이 실제로 약자인 경우 맥주를 사이다보다 선호해야 한다. 그런데 이는 ‘사실이 아니다’, 어차피 시비는 걸린다고 할 때 맥주를 먹으면 0의 보수를 얻는 반면 자신이 좋아하는 사이다를 마시면 1의 보수를 얻기 때문이다. 그러므로 총잡이 2의 신념체계는 직관적으로 옳지 않다.
그러므로 가정 D 및 $b>0.5$ 조건 하의 완전베이즈균형은 비직관적인 신념에 근거하기 때문에, 배제되어야 한다.
[가정 D를 따르고 $b<0.5$ 인 (총잡이 1이 약자일 확률이 더 높은) 경우]
이 때 총잡이 2의 기대보수는 시비를 걸 때 더 높으므로 총잡이 2는 시비를 건다. 총잡이 1은 총잡이 2의 이러한 생각을 합리적으로 예상할 수 있다. 따라서 총잡이 2가 사이다를 보면 시비를 건다는 걸 염두에 두고 뭘 마실 지 결정한다.
이 경우 ‘가정 D 하에서 그러지는 않겠지만 만약 자신이 사이다 대신 맥주를 마신다면 총잡이 2가 어쩔 것인가’ 에 따라 맥주와 사이다 중 무엇이 더 나은 선택인지가 결정된다.
만약 총잡이 2가 맥주를 보고 시비를 건다면, 총잡이 1은 자신이 약할 경우 가정 D대로 사이다를 마시는 게 좋다. 어차피 뭘 해도 시비를 걸리는데, 좋아하는 사이다를 마시는 것이 보수가 더 높기 때문이다 (맥주 마시면 0, 사이다 마시면 1). 그러나 자신이 강할 경우 ‘가정 D와 달리’ 맥주로 바꾸는 게 좋다. 어차피 시비가 걸린다면 좋아하는 맥주라도 마시는 것이 보수가 더 높기 때문이다 (맥주 마시면 1, 사이다 마시면 0).
만약 총잡이 2가 맥주를 보고 피한다면, 총잡이 1은 자신이 강할 경우 ‘가정 D와 달리’ 사이다 대신 맥주를 마시는 게 좋다. 좋아하는 맥주도 마시고 싸움도 피할 수 있기 때문이다 (맥주 마시고 싸움 피하면 3, 사이다 마시고 시비 걸리면 0). 한편 총잡이 1 자신이 약할 경우에도 사이다 대신 맥주를 마시는 게 좋다. 좋아하는 사이다는 못 마시지만 싸움을 피할 수 있기 때문이다 (맥주 마시고 싸움 피하면 2, 사이다 마시고 시비 걸리면 1).
따라서 가정 D (강자든 약자든 사이다) 하에서 b<0.5 (약자일 확률이 더 높음) 인 경우 총잡이 2가 할 행동 (사이다를 보고 시비 검) 을 전제로 한 총잡이 1의 최선의 행동은 어떤 경우에도 가정 D와 같지 않다. 따라서 가정 D 및 $b<0.5$ 조건 하에서는 완전베이즈균형이 성립하지 않는다.
결론
총잡이 2가 보기에 총잡이 1이 강자일 확률이 더 높으면, 완전베이즈균형 하에서 총잡이 1은 자신의 유형이 강자이든 약자이든 맥주를 마시고, 총잡이 2는 맥주를 보면 싸움을 피하되 혹시라도 사이다를 보면 시비를 건다.
총잡이 2가 보기에 총잡이 1이 약자일 확률이 더 높으면, 완전베이즈균형이 성립하지 않는다.