내 Applied Energy 논문의 수학 설명 - 도심지 건축물 신재생 확대 영향 분석 시의 계산비용 절감
필자가 국제학술지 Applied Energy (IF: 11.4)에 게재한 논문들 중 두 번째 논문의 주제는, ‘건축물에 설치되는 신재생에너지의 보급 확대 시의 도시 단위 영향 추정’을 보다 적은 계산비용으로 수행하는 방법이다.
(조금 자기PR 하자면, Applied Energy의 Impact Factor는 2020년 이전에도 7~8이었고 지금은 10이 넘으며, SJR에서 Energy(Miscellaneous) 부문에 속하는 100개 이상의 저널들 중 한 자리 등수를 유지해오고 있다. 필자의 논문들도 지금까지 각각 10번 이상 인용되었다.)
논문 배경
건축물에 태양광/ 태양열/ 지열히트펌프/ 연료전지 등을 설치해서, 건물의 전기부하/ 냉난방부하 중 일부를 자체적으로 충족할 수 있다. 또한 이 중 꼭 한 가지만이 아니라 둘 이상을 설치할 수도 있다. 이를테면 지붕에는 태양광과 태양열을 설치하고, 건물 내 공간에 연료전지를 설치하는 식이다.
이러한 신재생에너지시스템의 ‘최적’ 구성은 건물마다 다를 것이다. 전기를 많이 쓰며 옥상 면적이 넓고 온수는 그리 많이 쓰지 않는 곳에는 태양광과 연료전지가 적합할 것이고, 반대로 열 부하가 매우 많은 곳은 태양열과 지열히트펌프가 적합할 것이다.
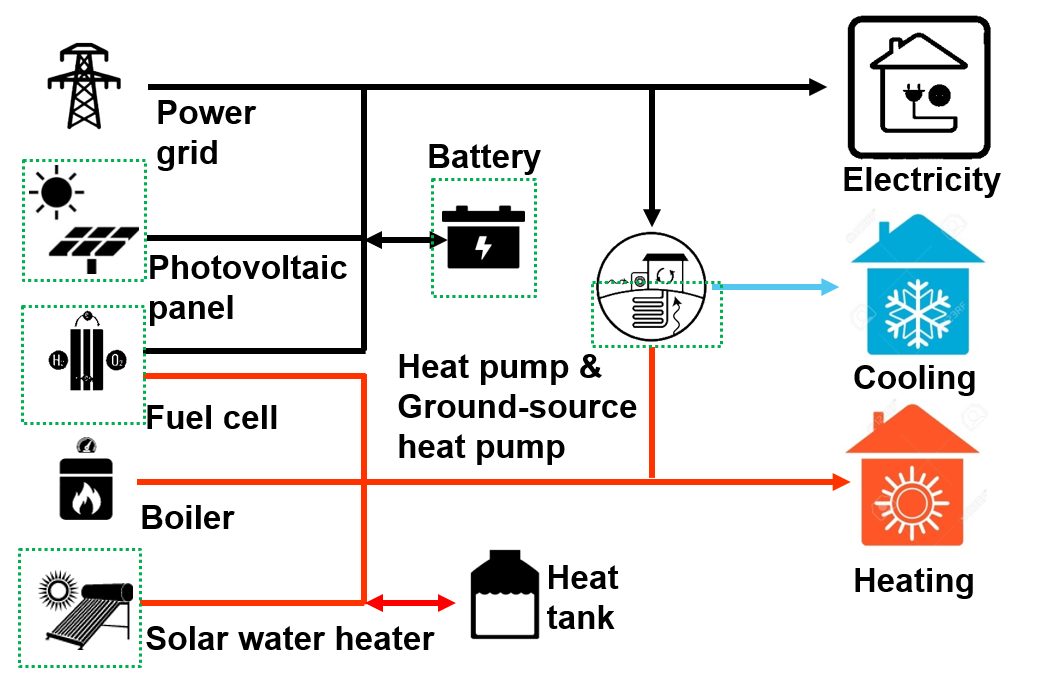건축물 내 융복합 신재생에너지시스템 도식도. 태양광/ 태양열/ 지열히트펌프/ 연료전지/ 배터리/ 열저장조로 구성됨.
건축물 내 신재생에너지 설치는, 일정 규모 이상의 신축/ 증축/ 개축 공공건물에 대해서 10년 전부터 의무화되었으며 그 의무비율이 점차 증가해왔다.
또한 서울시에서는 민간건물에 대해서도 (신축/ 별동 증축/ 전면 개축이면) 일정 규모 이상일 경우 신재생에너지 설치를 의무화하고 있다.
그러므로 필자는, 향후 신재생에너지 의무화가 어떤 도시 내에서 민간건물들 대다수로 확대될 경우의 영향을 추정한다면, 관련 policymaker들에게 중요한 정보가 될 수 있으리라 생각했고 이를 연구 주제로 삼았다.
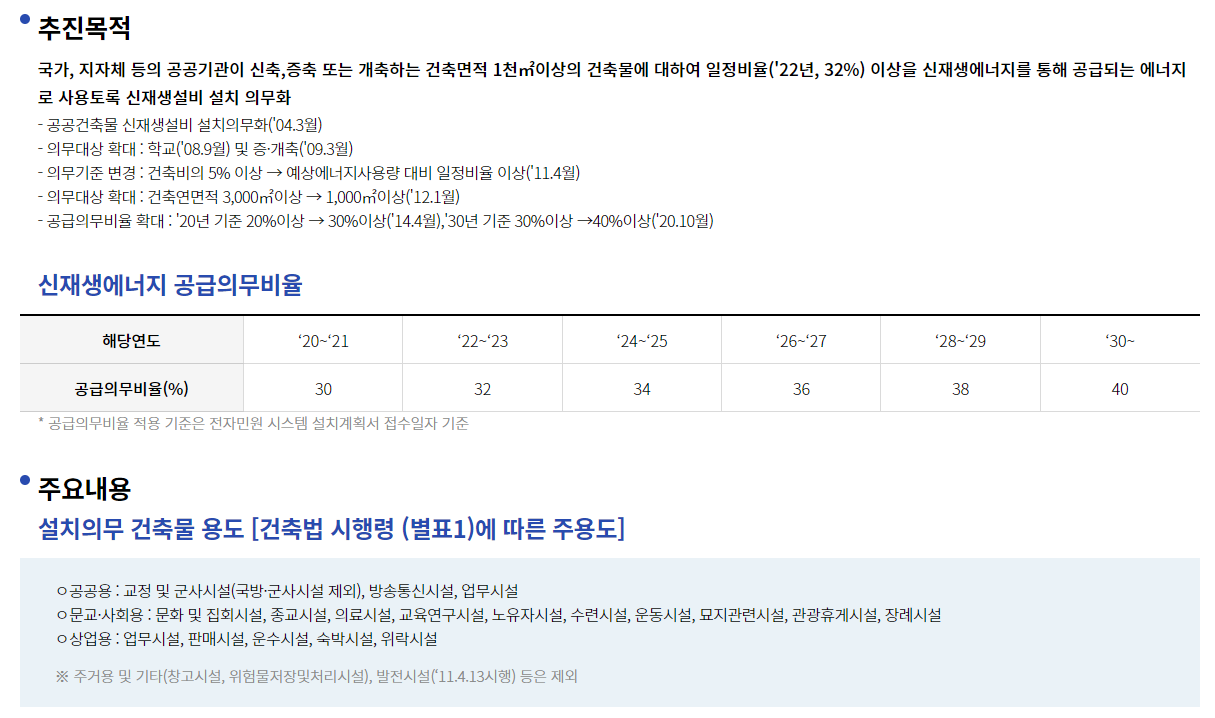공공건물 신재생에너지 설치의무화 사업내용. (출처: 한국에너지공단 신ㆍ재생에너지센터)
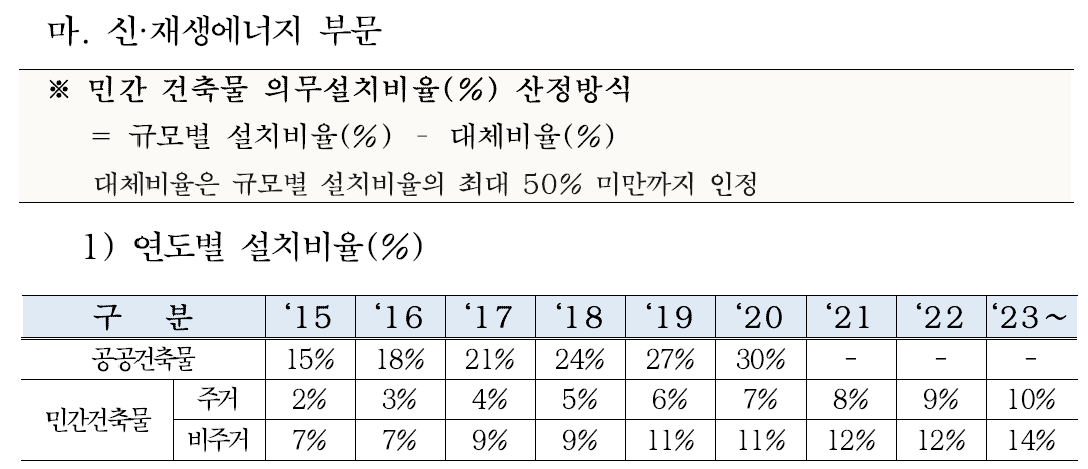서울특별시 녹색건축물 설계기준 중 신재생에너지 설치 관련 내용
계산비용 이슈
어떤 도시의 수만~수십만 개의 건물들 개별의 시간별 전기/ 난방/ 냉방 에너지 사용량을 추정할 수 있고 지붕 면적을 알고 있다고 하자. 그러면 각 건물별 최적 신재생에너지 구성을 다 계산하고 합산해서, 도시 내에 보급될 건물 신재생에너지의 용량 및 이로부터의 에너지공급량이 얼마일지 추정할 수 있고, 계통으로부터의 전기/가스 유입량의 감소분이 얼마인지도 추정할 수 있다. 심지어 전기 유입량의 증감은 시간 단위로도 추정할 수 있을 것이다.
그런데, 최적화 계산을 수십만 개 건물 각각에 대해 다 하는 데는 시간이 너무 많이 걸린다.
최적화 문제를 나름 현실적으로 모델링한 경우 변수 수와 제약조건 수가 10만개가 넘어가고 정수 변수도 포함될 수 있다. 이를 흔히 연구실에서 사용하는 MATLAB의 Optimization Toolbox로 (CPLEX/ Gurobi 같은 값비싼 상용 solver 없이) 푸는 데는, 하나 당 분 단위의 시간이 걸린다. 대략적인 예시로 10만을 1440 (24시간 x 60분)으로 나누면, 무려 69.4일이다.
그렇다면, clustering 기법을 써서 ‘비슷한’ 건물들을 cluster로 묶고 각 cluster 별 centroid에 대응하는 건물에 대해서만 최적화 계산을 한다면 어떨까? 최적화 계산 횟수가 수백~수천 번 정도로 줄어들 것이다.
그리고 centroid에 대해 계산된 신재생에너지 용량/ 에너지 공급량에 건물 면적 비 등을 가중치로 곱하면 각 건물들의 최적 신재생에너지 구성에 대한 근사결과를 도출할 수 있을 것이고, 그 근사결과들의 ‘모든 건물들에 대한 총 합’은 건물 하나하나에 대해 직접 최적화 계산을 수행해 얻은 총 합과 비슷하지 않을까?
즉, 건축물 신재생에너지 의무화가 도시 내 대부분의 건물들에 확산될 경우의 영향을 최적화기법 기반으로 계산하는 데 드는 계산비용이 큰데, 이를 clustering을 이용해서 크게 줄여보자는 것이 필자의 아이디어였다.
비슷한 건물끼리 Clustering
그러면 clustering의 기준으로 삼을 건물의 feature를 정해야 한다. 그래야 feature space에서 grid를 만들든, k-means를 사용하든 해서 cluster들을 결정할 수 있기 때문이다.
이 때 건물의 규모 자체, 즉 에너지 사용량이나 연면적 자체를 feature로 정하지 않으려 했다. 어떤 두 수 간의 상대비율을 feature로 정하려 했다. 이러한 결정에는, 박사과정 당시 지도교수님께서 항상 non-dimensional parameter를 쓰라고 말씀하셨던 영향이 컸다.
필자는 주거용 건물에 대해서는 ‘가구수 당 연면적’ 과 ‘가구수 당 지붕면적’ 두 개를 feature로 설정했다. 그리고 feature space에서 2차원 등간격 grid를 만들고 각 grid box의 중심별로 1가구에 대응하는 연면적과 지붕면적을 갖는 건물의 최적 신재생구성을 계산 후, 같은 grid box 내에 속한 건물들에 대해서는 각 건물의 가구수를 곱해서 근사적 신재생구성을 얻었다.
이 경우 실제 주거용 건물 수가 수만개에 달하더라도, 최적화 계산은 grid box의 개수만큼만 수행된다.
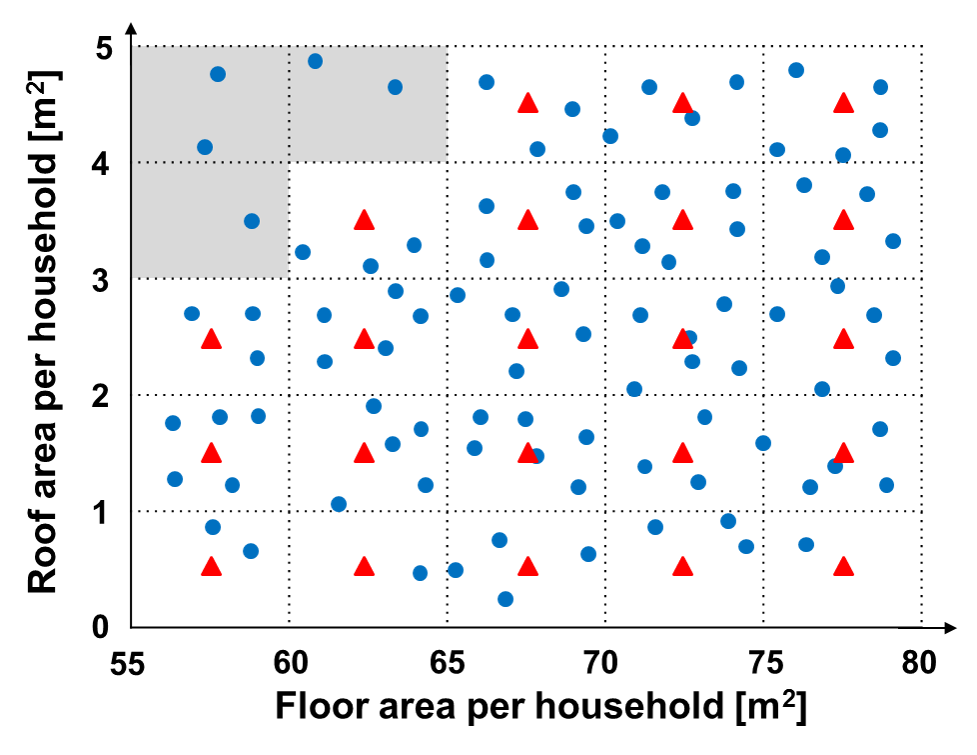주거용 건물에 대한 clustering 도식도.
비주거용 건물에 대해서는 다른 feature들을 설정했다. 먼저 1년 12개월 간 월별 전기 사용량 및 가스 사용량 그래프의 ‘모양’들을 feature로 설정했다 (아래 그림 참고).
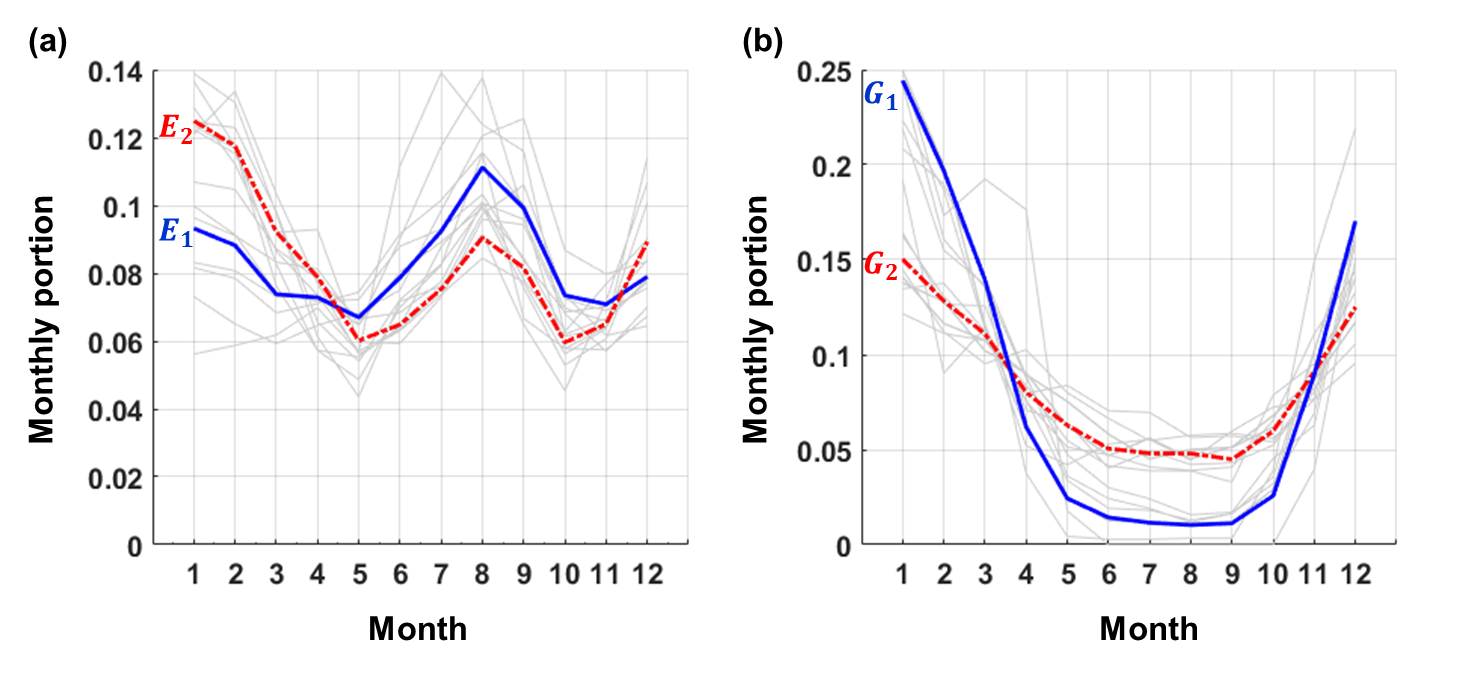비주거용 건물들의 월별 전기/가스 사용 추이, 그리고 추이 기반 clustering 시의 centroid들.
건물 $i$의 12개월 간 월별 전기 사용량 벡터와 가스 사용량 (12차원) 벡터를 각각 $e_i$와 $g_i$라 하자. 그러면 위 그림의 옅은 회색 선은 각각 $e_i / \Vert e_i \Vert_{1}$과 $g_i / \Vert g_i \Vert_{1}$이다. 위 그림을 보면 각 비주거용 건물별로 월별 에너지 사용량의 모양이 제각각이다 (옅은 회색 선들). 이들을 k-Means를 이용해 12차원 벡터들을 두 개의 cluster로 분류하고, 각 건물들이 속하는 cluster centroid의 모양을 갖는다고 가정했다 (파란 선과 빨간 선).
다음으로는 ‘가스 사용량 대 전기 사용량의 비율’을 feature로 설정했다. 마지막으로, 앞의 두 feature 기반 cluster들의 centroid 별로 지붕 면적이 충분히 크다고 가정할 경우에 도출된 용량의 태양광과 태양열 설비가 차지하는 지붕면적을 구하고, 그 지붕면적보다 실제 지붕면적이 작을 경우 그 상대비율을 feature로 설정했다.
이 때 두 비율들로는 등간격 grid를 만들지 않고, 각 feature에 대해 일정 수의 구간들을 만들기로 하고 그 구간들의 boundary를 구하는 최적화 문제를 세팅했다. 등간격으로 할 경우 cluster 별로 속하는 건물 숫자의 불균형이 매우 심할 것이라 생각했기 때문이다.
예를 들면 가스-전기 비율 구간에 대한 최적화 문제를 보자.
건물 $i$가 속한 cluster $C_k$의 가스-전기 비율의 centroid 값을 $\mu_{k}$ 하자. 그러면 건물 $i$의 실제 가스 사용량은 $\Vert g_i \Vert_{1}$이지만, 추정된 가스 사용량은 $\mu_{k} \Vert e_i \Vert_{1} $이다. 즉 $ \mu_k \Vert e_i \Vert_{1} - \Vert g_i \Vert_{1} $ 는 `오차항’이다.
한편 $\mu_{k}$는 해당 cluster 내 모든 건물들의 가스 사용량의 합을 전기 사용량의 합으로 나눈 값이어야 한다. 그리고 $g_i/e_i$의 값은 해당 cluster의 전기-가스 비율의 boundary 값들인 $v_{k-1}$과 $v_{k}$ 사이의 값이어야 한다. 이 때 boundary 값들은 미리 정해진 값이 아니다. Boundary 값들을 정하면 각 cluster에 속하는 건물들의 집합이 결정되고, 그러면 $\mu_{k}$는 자동으로 계산된다.
그러므로 boundary 값들 $v_{1}, v_{2}, \cdots, v_{K-1}$ 을 구하기 위한 최적화 문제는 아래와 같이 정의된다.
Minimize $ \sum_{k=1}^{K} \sum_{i \in S_k} | \mu_k \Vert e_i \Vert_{1} - \Vert g_i \Vert_{1} |$
Subject to
$ \mu_{k} = [\sum_{i \in S_k} \Vert g_i \Vert_{1}]/[ \sum_{i \in S_k} \Vert e_i \Vert_{1}] $
$ v_{k-1} \leq \Vert g_i \Vert_{1} / \Vert e_i \Vert_{1} \leq v_{k} $
$ v_{0} = 0, v_{K} = \infty$
이 때 목적함수가 오차항의 제곱합이 아니라 절대합인 이유는, 소수의 가스-전기 비율이 매우 큰 건물들의 영향이 지나치게 커지는 걸 방지하기 위함이다.
필자의 논문 케이스에 대해 구간을 5개로 정하고 위 문제를 푼 결과는 아래 그림과 같다.
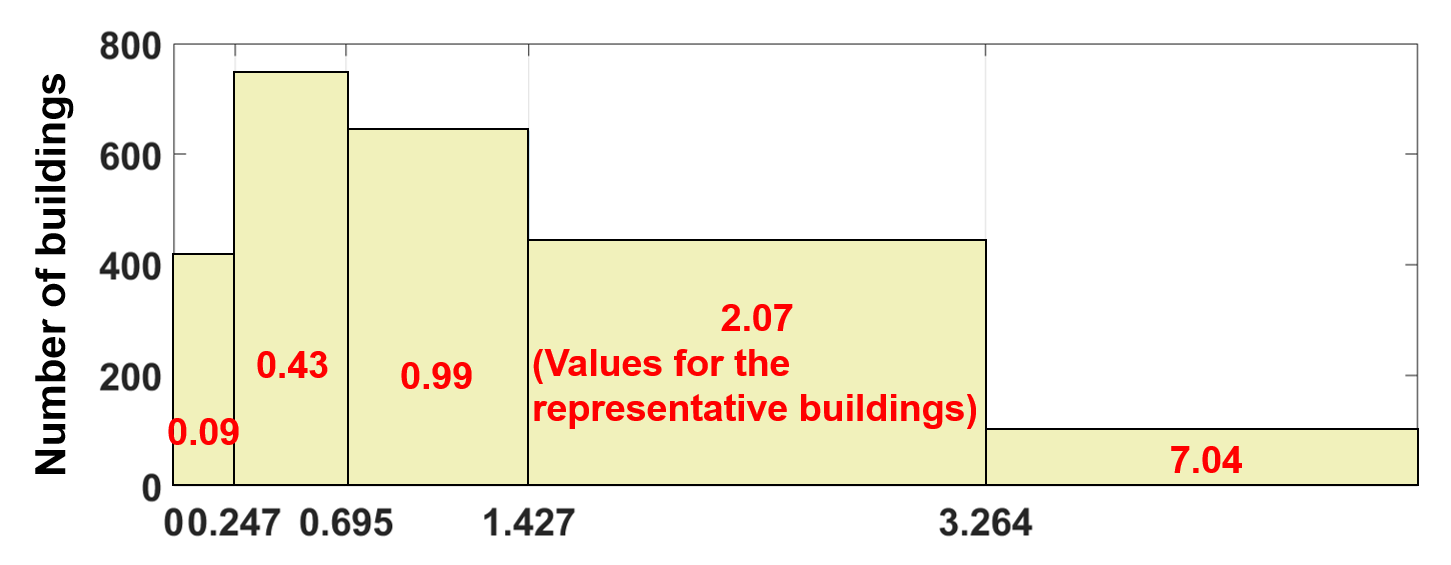비주거용 건물의 연간 가스사용량과 전기사용량의 간 상대비율 기반 clustering.
지붕면적 구간에 대해서도 같은 맥락으로 최적화 문제를 정의하여 구간 별 boundary 값들을 얻는다. (여담으로 연구 당시에는 회귀분석에 대해 깊은 지식이 없어서 인지를 못 했는데, 지금 보니 회귀분석과 다르면서도 비슷한 문제 세팅인 것 같다.)
필자는 월별 전기사용량 모양에 대해 대표 모양 2개, 가스에 대해서도 대표 모양 2개, 그리고 가스-전기 사용량 비율에 대해서 구간 5개, 지붕면적 구간 4개를 정했다. 그리고 건물 용도 (근린생활/ 업무/ 판매/ 의료 등) 별로 cluster를 달리 배정했다. 단, 가스를 사용하지 않는 건물들도 있어 이들에 대해서는 전기사용량 모양과 지붕면적 구간만 feature가 계산된다. 이 경우, 각 건물 용도별 cluster의 수는 2 x 2 x 5 x 4 + 2 x 4 = 88개이다.
즉, 업무용 건물이 실제로는 수천개에 달하더라도, 필자의 분석에서 업무용 건물에 대한 최적화 계산은 88회만 수행된다. 만약 cluster centroid 건물의 연면적을 $A_{0}$라 가정하고 최적 신재생 구성을 얻었다고 하자. 그러면 건물 $i$의 연면적을 $A_{i}$라 할 때, 건물 $i$에 대한 최적 신재생 구성의 근사치는, centroid에 대한 계산 결과에 $A_{i}/A_{0}$을 곱한 값이다.
(정확히는 이 방법을 쓰려면 최적화 문제가 linear problem이어야 하며, 필자는 선형계획법을 적용했기 때문에 이 조건이 성립한다.)
Clustering 적용 결과
필자의 논문에서는 validation case로써 4,425개의 주거용 건물들을 957개의 cluster들로, 2,779개의 비주거용 건물들을 176개 cluster들로 분류했다. 아래 그림에서 보듯, clustering 후 cluster 별 centroid들에 대해서만 최적화 문제를 풀어 (즉 계산비용을 줄여서) 얻은 결과 (빨강)와, 각각의 건물에 대해 개별적으로 최적화 문제를 풀어 얻은 결과 (파랑) 가 꽤나 비슷하다.
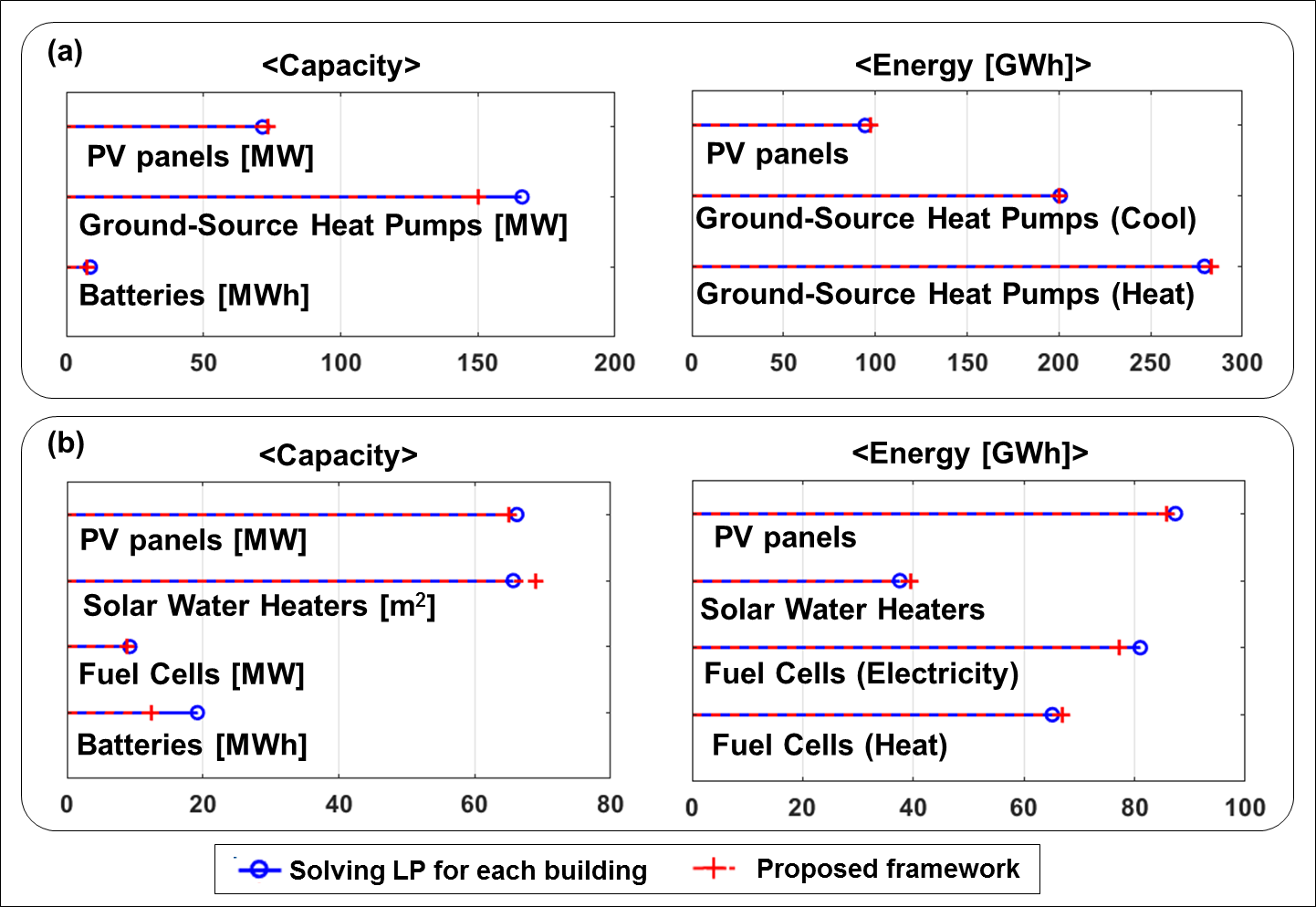특정 구역에 대한 건물 신재생에너지 확산 영향 추정 비교. 각 건물에 대해 최적화 문제를 풀었을 때의 결과와, 필자가 제안한 방법 기반으로 계산비용을 줄여 계산했을 때의 결과가 매우 유사함.
논문의 후반부에서는, 서울의 500m2 이상 건물들에 대해 신재생에너지 설치 의무화가 특정 의무비율로 적용된 경우의 예상 보급 실적 및 에너지 계통에의 영향, 그리고 의무비율 변화에 따른 예상 탄소 저감량을 위 방법에 기반해 추정했다. 이 분석의 깊이 자체는 별로 깊지 않아서, 어디서 자랑할 수준은 못 된다고 본다.
그러나 필자의 연구는, 아주 많은 수의 소규모 분산형 에너지시스템들이 증가할 때 그 효과를 분석하는 parametric study를 하기 위한 프레임워크로써의 가치는 있다고 본다.
이러한 정책적 효과 관련 시뮬레이션 연구는, 여러 가지 파라미터들 (의무화 비율, 신재생에너지 원별 단가 등) 을 이 값 저 값으로 바꾸면서 결과들을 도출한 후 분석하는 parametric study 방식으로 진행되기 마련이다. 위에서 언급한 `의무비율 변화에 따른 예상 탄소 저감량’ 또한 parametric study이다.
그런데 하나의 case를 계산하는 데 시간이 오래 걸리면, 이러한 parametric study는 거의 불가능에 가깝다. 필자의 프레임워크를 사용하면, 하나의 case를 계산하는 데 걸리는 시간을 크게 단축할 수 있고, 그 결과 parametric study를 할 수 있다.