내 Applied Energy 논문의 수학 설명 - ‘가짜’ curtailment 문제
필자가 국제학술지 Applied Energy (IF: 11.4)에 게재한 논문들 중 첫 번째 논문의 주제는, ‘태양광/ 풍력/ ESS를 포함한 고립계통에서 재생에너지 출력제한(curtailment)의 총량에 상한을 둘 경우’에 대한 최적화 문제 세팅 및 분석이다.
(조금 자기PR 하자면, Applied Energy의 Impact Factor는 2020년 이전에도 7~8이었고 지금은 10이 넘으며, SJR에서 Energy(Miscellaneous) 부문에 속하는 100개 이상의 저널들 중 한 자리 등수를 유지해오고 있다. 필자의 논문들도 지금까지 각각 10번 이상 인용되었다.)
논문 배경
출력제한은 필자가 논문을 쓰던 2018년에는 ‘가까운 미래의 일’ 정도로 생각되었으나, 최근에는 실제로 이슈가 되고 있다.
대략 2021년 즈음부터 제주도에서 태양광과 풍력의 출력제한이 본격적으로 증가하며 언론에 보도되기 시작하였고, 재생발전 출력제한에 따른 사업자들의 손실 우려 및 보상 방안에 대한 논의가 필요한 상황이다. (출력제한 이슈에 관심이 있는 독자는 에너지경제연구원의 관련 연구를 참고하길 바란다.)
 2020년대 들어서, 제주도 재생발전의 출력제한 문제가 대두되고 있음.
2020년대 들어서, 제주도 재생발전의 출력제한 문제가 대두되고 있음.
이 포스팅에서는, 위 논문에 사용한 직관 및 수학 내용을 정리해 본다.
대상 에너지시스템은 태양광 + 풍력 + 디젤 + ESS로 전기부하를 공급하며 중앙계통과는 분리되어 있다 (녹색섬이라 생각하자). 혹시 재생발전량이 0이더라도, 디젤발전기만으로 부하 충당 자체는 가능하다. 반대로 재생발전량이 너무 많아 부하 충족은 물론 ESS 완충까지 하더라도 전기가 남을 경우 이는 특별한 용도 없이 dump load에서 소비된다, 즉 출력제한(curtail)된다. 이 때 녹색섬이라 불리려면, 전체 전기에너지 수요의 일정 비율은 재생발전으로 충당해야 한다.
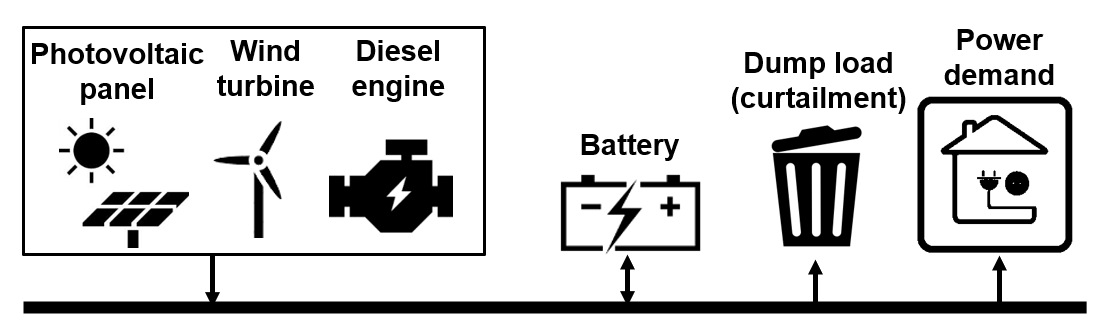 태양광/ 풍력/ 디젤/ ESS로 이루어진 섬 전기 공급 시스템 도식도. 잉여전력을 버릴 수 있음.
태양광/ 풍력/ 디젤/ ESS로 이루어진 섬 전기 공급 시스템 도식도. 잉여전력을 버릴 수 있음.
최적화 문제
그러면 태양광/ 풍력/ ESS는 각각 어느 정도의 용량으로 설치해야 할까? 이는 특정 기간의 시간별 전기부하, 일사량, 풍속을 input 자료로 사용하여, 재생발전기 초기설치비용과 운영기간 내 디젤 연료비의 총 합을 최소화하는 태양광/ 풍력/ ESS 각각의 용량을 도출하는 최적화 문제를 풀어서 결정할 수 있다. 수식은 아래와 같다.
Minimize $c_{\text{pv}} s_{\text{pv}} + c_{\text{wt}} s_{\text{wt}} + c_{\text{batt}} s_{\text{batt}} + c_{\text{diesel}} \sum_{t} p_{\text{diesel}}[t]$
Subject to
$p_{\text{load}}[t] = p_{\text{diesel}}[t] + s_{\text{pv}} p_{\text{pv}}[t] + s_{\text{wt}} p_{\text{wt}}[t] + p_{\text{disch}}[t] – p_{\text{ch}}[t] – p_{\text{curtail}}[t] \quad \forall t$
$e_{\text{batt}}[t+1] = e_{\text{batt}}[t] + \mu p_{\text{ch}}[t] – p_{\text{disch}} /\mu \quad \forall t$
$ e_{\text{batt}}[t] \leq s_{\text{batt}} \quad \forall t$
$ p_{\text{ch}}[t] \leq \gamma s_{\text{batt}} \quad \forall t$
$ p_{\text{disch}}[t] \leq \gamma s_{\text{batt}} \quad \forall t$
$ p_{\text{ch}}[t] p_{\text{disch}}[t] = 0 \quad \forall t$
$ \sum_{t} p_{\text{diesel}}[t] \leq (1-\alpha_{\text{renewable}}) \sum_{t} p_{\text{load}}[t] $
위에서 $c$는 비용, $s$는 용량, $p$는 전력, $e$는 저장된 에너지, $\mu$는 효율, $\alpha$는 규정 비율이며, pv는 태양광, wt는 풍력, batt는 배터리, load는 부하, diesel은 디젤엔진, ch는 충전, disch는 방전, dump는 출력제한이다. $s_{\text{wt}}$는 풍력 발전기의 대수이므로 음이 아닌 정수(nonnegative integer)이며, 나머지는 음이 아닌 실수들이다. 비용은 태양광/ 풍력/ 배터리에 대해서는 단위 용량당 초기투자비, 디젤에 대해서는 연료비이다.
이 문제에서 도출한 태양광/ 풍력/ 배터리 용량은, 디젤 발전기를 통해 공급되는 전기에너지의 비중이 전체의 $1-\alpha_{\text{renewable}}$ 이하가 되게 만드는 용량이다. 이를테면 $\alpha_{\text{renewable}}=0.6$인 경우, 연간 총 전기에너지 수요 중 최대 40%까지만 디젤 발전기로 충당될 수 있다는 제약 하에 시스템 구성을 도출한다.
충전/방전: 같은 시간엔 둘 중 하나는 0이어야
위에서 제약조건 $ p_{\text{ch}}[t] p_{\text{disch}}[t] = 0$ 은, 한 time step 내에서 ESS는 충전 또는 방전 둘 중 하나만을 수행한다는 제약이다. 충전항과 방전항이 동시에 양수가 되지 않도록 두 항 간 곱이 0이라는 제약을 둔다.
문제는, 이 제약조건이 비선형 등호제약이므로 non-convex 최적화 문제가 된다는 것이다. Non-convex 최적화 문제는 일반적으로 global optimum을 달성하기 매우 어렵다.
만약 아래와 같이 충분히 큰 양수 $M$과 시간별 이진수 $x[t]$를 도입하면, 정수선형계획 (Mixed-integer Linear Programming, MILP) 문제가 되므로 선형계획법에 특화된 solver를 적용할 수는 있다.
$ p_{\text{disch}}[t] \leq M x[t]$, $p_{\text{ch}}[t] \leq M (1-x[t]) \quad \forall t$
그러나 이 경우, 이진수가 너무 많아져서 계산 시간이 매우 오래 걸린다 (일반적으로 정수 변수가 많으면, 해당 정수 변수들의 조합별로 해를 탐색하는 과정이 필요해 시간이 오래 걸린다).
이 문제를 해결하는, 구체적으로는 시간별 이진수 없이 풍력 용량 정수변수만 있는 (즉 풀기 쉬운) MILP 문제로 만들면서도 거의 같은 답을 얻는 방법이 있다.
위 비선형 등호 제약을 없애는 대신, 아래와 같이 목적함수에 충전항과 방전항에 아주 작은 양수계수를 곱한 항들의 합 $ \epsilon \sum_t ( p_{\text{disch}}[t] + p_{\text{ch}}[t] ) $ 을 penalty term들로써 추가하는 것이다.
위 penalty term이 추가된 목적함수를 최소화하기 위해, 같은 time step에 대한 충전 $p_{\text{ch}}[t]$과 방전 $p_{\text{disch}}[t]$ 둘 중 하나는 0이 된다.
Curtailment 총량 상한 제약 추가 시 발생한 문제
위 최적화 문제에 재생발전 curtailment의 총량에 상한을 두는 제약을 아래 수식과 같이 추가할 수 있다. (제주도에서 curtailment 총량이 늘어나는 데 대한 문제의식이 생기면서 향후 이런 제약조건이 추가된 문제들이 본격적으로 연구될 수도 있다)
$ \sum_{t} p_{\text{curtail}}[t] \leq \alpha_{\text{curtail}} \sum_{t} p_{\text{load}}[t] $
필자는 이 제약을 추가 시, 충전과 방전에 양수계수를 곱한 penalty term들을 목적함수에 추가해도 충전항과 방전항이 둘 다 양수가 되는 문제가 발생함을 발견했다. 필자가 다뤘던 케이스에서는 총 8,760시간 중 2,275시간에서 $ p_{\text{ch}}[t] p_{\text{disch}}[t] > 0$ 이었다.
필자의 분석 결과, 이는 충전과 방전 간 차이 $p_{\text{ch}}[t]-p_{\text{disch}}[t]$ 가 같을 때 둘 다 0보다 커질수록 생기는 일종의 ‘가짜’ curtailment 효과이다.
이를테면 $p_{\text{ch}}[t]-p_{\text{disch}}[t]=a$라 하면 (충전), 정상적인 답에서는 $p_{\text{ch}}[t]=a, p_{\text{disch}}[t]=0$이어야 한다. 그러나 만약 $p_{\text{ch}}[t] = a+b, P_{\text{disch}}[t] = b$, 즉 충전과 방전 모두에 $b$가 더해진 경우 어떻게 될까?
배터리 내 에너지의 변화를 $\triangle e(P_{\text{ch}}[t], p_{\text{disch}}[t]) = e_{\text{batt}}[t+1] – e_{\text{batt}}[t] = \mu p_{\text{ch}}[t] - p_{\text{disch}}[t]/\mu$라 하면, $\triangle e(a+b,b) - \triangle e(a,0) = b (\mu – 1/\mu) < 0$ 이 된다 ($0<\mu<1$ 이니까). 즉, 충전과 방전 모두에 $b$가 더해지면 충전에 의한 배터리 내 에너지 증가분이 $b (\mu – 1/\mu)$ 만큼 더 작게 계산된다.
$p_{\text{ch}}[t]-p_{\text{disch}}[t]=-a$, 즉 방전시에도 결과는 마찬가지다. 똑같이 $\triangle e(a+b,b) - \triangle e(a,0) = b (\mu – 1/\mu) < 0$ 이 되어, 방전에 의한 배터리 내 에너지 감소분이 $b (\mu – 1/\mu)$ 만큼 더 크게 계산된다.
즉 문제가 없을 때의 답과 비교하면 배터리 내 저장된 에너지의 양이 $b (\mu – 1/\mu)$만큼 사라지는 것처럼 계산되는데, 이는 실제로 dump load에서 소비된 것은 아니기 때문에 ‘가짜’ curtailment라고 이름붙였다.
문제의 원인 및 해결책
이 문제는 왜 발생하는 걸까?
이런 가짜 curtailment가 발생하면, 배터리에 저장된 에너지가 줄어든다. 이는 에너지를 저장하기 위해 요구되는 배터리의 용량도 줄어든다는 뜻이다. 배터리는 비싼 설비이기 때문에, 배터리에 저장된 에너지를 ‘가짜로’ 잃더라도 배터리 용량을 줄일 수 있다면, 해당 solution이 ‘목적함수를 최소화’하게 된다.
그래서 ‘수학적으로 목적함수가 최소화되는’ 해를 찾는 과정에서 저런 문제가 발생하는 것이다. 실제로 한 case에 대해 계산 결과 원래는 배터리 용량이 220 kWh로 도출되어야 하나, 가짜 curtailment 문제가 발생한 경우 178 kWh로 도출되었다.
필자는 이 문제를 해결하기 위해, 아래와 같은 프로세스를 제안하였다. correct solution에서는 모든 시간 각각에 대해 충전항과 방전항 둘 중 하나는 0임에 착안해, 조건들에 따라 각 시간별 충전항, 방전항들 중 특정 항의 upper bound를 강제로 0으로 만드는 과정을 반복한다.
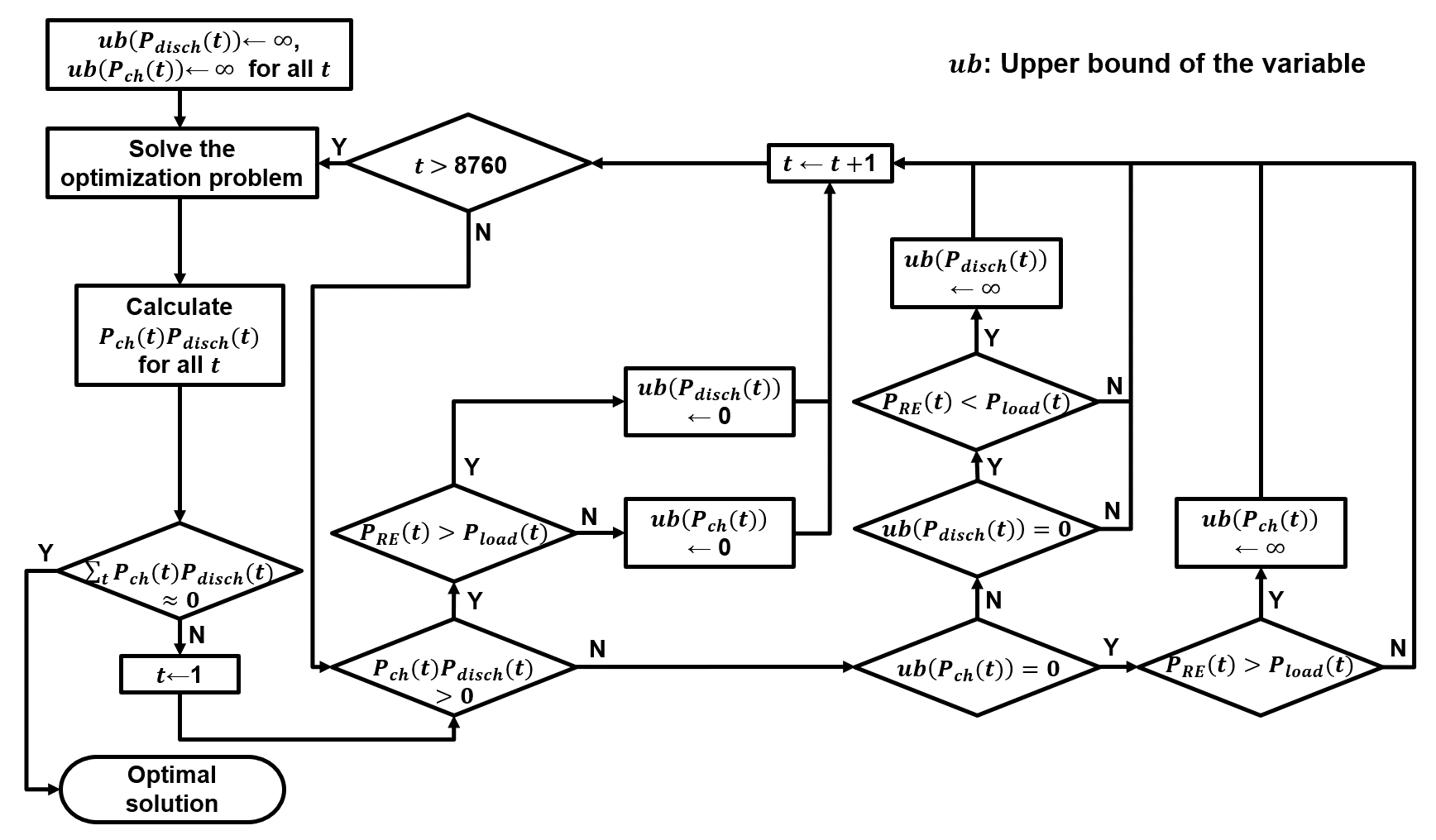 필자가 제안한, 출력제한의 총량 제약이 있더라도 동시 충/방전 문제가 없는 solution을 얻도록 하는 flowchart.
필자가 제안한, 출력제한의 총량 제약이 있더라도 동시 충/방전 문제가 없는 solution을 얻도록 하는 flowchart.
이 방법을 쓰면, 시간별 이진수를 도입하지 않고도 5~30번 정도의 iteration이면 충분히 correct solution에 근접한 solution을 얻는 것을 확인하였다.
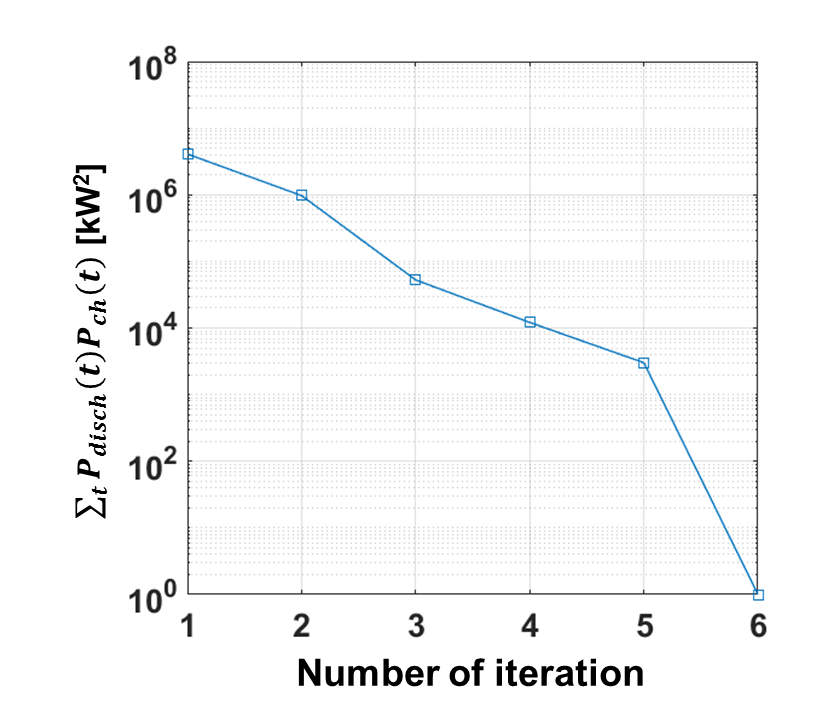 위 flowchart대로 수행 시, 몇 번의 iteration으로 동시 충/방전 문제가 없는 solution을 얻음.
위 flowchart대로 수행 시, 몇 번의 iteration으로 동시 충/방전 문제가 없는 solution을 얻음.