에너지정책의 효과를 ‘정량적으로’ 분석하는 방법으로, 회귀분석의 일종인 ‘패널 분석’ (Panel data analysis) 이 있다. 이를테면 에너지경제연구원에서는 에너지효율 R&D 투자가 에너지소비 감소에 기여했는지 여부를 검정하기 위해, “에너지효율향상 R&D 투자효과 분석 및 정책방향 연구” 를 수행한 바 있다.

해당 연구에서는 1985년부터 2013년까지 연도별로 12개 국가 각각의 에너지소비량/ R&D투자/ 통제대상변수들 데이터를 사용해, 에너지효율향상 R&D가 에너지소비량 절감에 유의미한 영향을 주었는지를 알아보았다. 이러한 데이터는 ‘여러 개체’ 를 ‘여러 시간’ 에 걸쳐 관측해 얻은 데이터이며, 이러한 데이터를 패널 데이터라고 한다.

이번 포스팅에서는, 필자가 패널데이터분석 실무 공부를 위해 해당 연구 결과의 복원을 시도한 결과를 정리하였다.


연구 상세

12개 국가 목록은 노르웨이/ 네덜란드/ 덴마크/ 독일/ 미국/ 스페인/ 스웨덴/ 영국/ 오스트리아/ 일본/ 포르투갈 이다.

해당 패널분석에서 반응변수는 ‘1인당’ 에너지 소비량이다. 설명변수들은 ‘1인당’ GDP/ 에너지 가격 지수/ 난방도일/ ‘1인당’ R&D 투자 축적량이다. 에너지 소비량에 큰 영향을 미치는 요소로 GDP/ 에너지가격/ 난방에너지사용량/ 인구수 가 있으므로, 이들을 통제한 상태에서 R&D투자의 효과를 계산하기 위함이다.

구체적으로는 변수들에 로그를 취해서 계수추정량이 탄력성을 의미하도록 하였다. 또한 명시적으로 반영하지 못한 변수들 (즉 오차항의 성분) 중 각 국가별로 시간에 관계없이 고유하게 가지면서 설명변수들과 상관된 요소가 존재할 수 있으므로 (이를테면 문화적 요소 등), 이를 고려한 고정효과 (fixed effect) 모델 및 1계차분 (first-order difference) 모델의 계수를 도출하였다.

고정효과 모델의 수식은 아래와 같다.

$\text{ln}(\frac{EC}{Pop})_{i,t} = \beta_0 + \beta_1 \text{ln}(\frac{GDP}{Pop})_{i,t} + \beta_2 \text{ln}(EP)_{i,t} + \beta_3 \text{ln}(HDD)_{i,t} + \beta_4 \text{ln}(\frac{AccRnD}{Pop})_{i,t} + u_i + e_{i,t}$

첨자 $i$와 $t$는 각각 나라와 연도를 의미한다. $EC$는 에너지 소비량, $Pop$는 인구수, $GDP$는 총 GDP, $EP$는 에너지 가격 지수, $HDD$는 난방도일, $AccRnD$는 해당 연도까지의 에너지효율 R&D 투자액의 축적량이다 (단, 모든 연도의 투자액을 단순히 더하지 않고 감가율을 적용하였다). 오차항에서 $u_i$는 시간에 관계없는 국가 고유의 요소들 (문화적 요소 등), $e_{i,t}$는 국가 및 시간별로 변하는 요소들을 의미한다.

1계차분 모델의 수식은 아래와 같다.

$\Delta \text{ln}(\frac{EC}{Pop})_{i,t} = \beta_1 \Delta \text{ln}(\frac{GDP}{Pop})_{i,t} + \beta_2 \Delta \text{ln}(EP)_{i,t} + \beta_3 \Delta \text{ln}(HDD)_{i,t} + \beta_4 \Delta \text{ln}(\frac{AccRnD}{Pop})_{i,t} + \Delta e_{i,t}$

해당 연구의 분석기간인 1985~2013년 중 1997년에 교토의정서가 채택되어, 해당 시기 전후로 에너지효율 R&D 투자에 양적/ 질적 차이가 나타날 가능성이 크다. 이를 고려해, 해당 연구에서는 1997년을 기준으로 전기와 후기를 나누어 각각에 대한 추정 및 모든 기간에 대한 변수별 계수추정을 수행하였다.

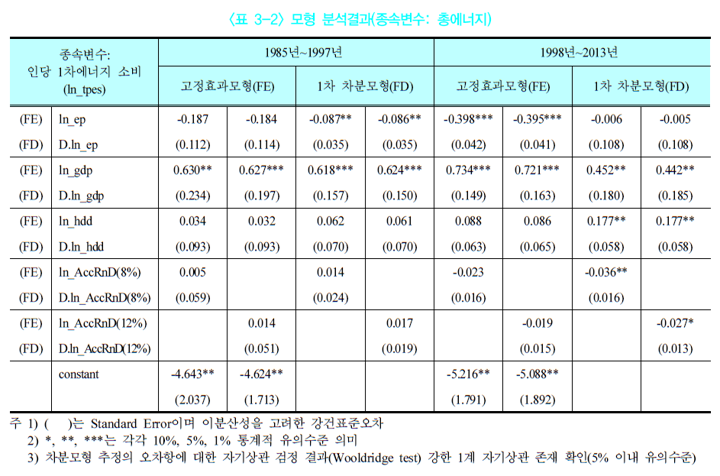systemscheme 해당 연구의 패널 분석 결과.

패널분석으로 도출한 변수 별 계수의 부호를 보면, 에너지가격은 음의 계수를, 1인당 GDP와 난방도일은 양의 계수를 갖는다. 일반적으로 에너지 가격이 상승하면 에너지 소비가 감소하고, GDP와 난방도일이 증가하면 에너지 소비가 증가할 것이라 예상하는데, 패널분석 결과가 예상과 일치한다.

에너지 효율 R&D 투자 축적은 전기에서는 계수가 통계적으로 유의하지 않았으나, 후기에서는 유의한 음의 계수를 가졌다. 이는 에너지 효율 R&D 투자가 에너지 절감에 기여한다는 예상과 일치하며, 그 효과가 교토의정서 채택 이후 본격적으로 나타났음을 의미한다.

(단, 고정효과 회귀와 1계차분 회귀의 계수들의 값들 및 유의성은 서로 다르다. 그래서 보통 두 회귀를 모두 수행 후, 부호가 일치하는지를 본다. 그리고 모든 항들에 자연로그를 취했으므로, 계수의 값은 ‘한 나라 내에서 다른 설명변수들의 불변 가정 하에 해당 설명변수가 현재 대비 1% 증가 시 반응변수의 퍼센트 기준 증감’을 의미한다.)


복원을 위한 데이터 수집

반응변수의 경우, OECD database의 1차에너지 (primary energy supply) 를 사용하였다. 설명변수들 중 GDP, 인구수, 에너지효율 R&D 투자액 또한 OECD database에서 찾은 값들을 사용하였다. 에너지효율 R&D 투자액 자료를 누적 축적량으로 변환하는 방법은 에너지경제연구원 문헌에서 설명한 방법과 같다.

에너지가격의 경우, 해당 연구에서 사용한 자료를 그대로는 얻을 수 없었다. IEA의 Energy prices and taxes Database가 유료회원 전용 자료이기 때문이다.

그래서, 에너지가격을 누락변수 (ommited variable) 라 할 때, 해당 누락변수와 상관관계가 있어 도구변수 (instrumental variable) 로 쓸 수 있으면서 OECD database에서 구할 수 있는 자료인, Crude oil import prices를 대신 사용하였다.

난방도일의 경우, 필자는 스위스/ 영국/ 일본 의 자료를 구할 수 없었다. (IHS와 IEEJ의 자료가 유료이며, 영국의 경우 EU에서 탈퇴하여 Eurostat에서 자료를 찾을 수 없었다.) 그래서, 최종적으로는 해당 3개 국가를 제외한 나머지 9개 국가에 대한 자료를 사용하였다.


복원 결과

필자가 모은 데이터로 고정효과 회귀를 수행해 도출한 계수별 부호가, 기존 연구 결과와 일치하였다. 교토의정서 이후 기간과 전체 기간에 대해, R&D 투자액 축적과 에너지가격에 대해서는 음의 계수가, GDP와 난방도일에 대해서는 양의 계수가 유의미하게 도출되었다 (클러스터 표준오차 기준).

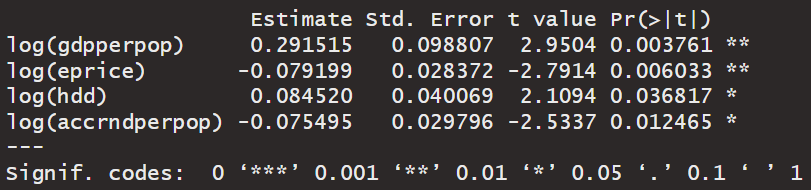
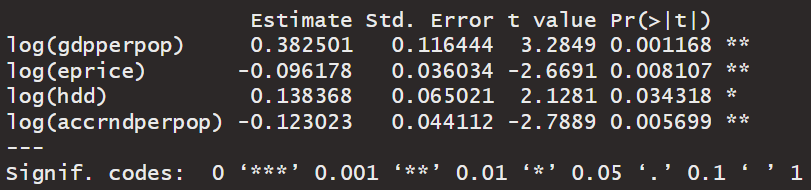systemscheme systemscheme 필자가 모은 데이터로 fixed effect 회귀를 수행한 결과. (위: 교토의정서 이후 기간, 아래: 전체기간)

Hausman test를 통해, 임의효과 (random effect) 가 아닌 고정효과 회귀를 수행해야 함도 확인하였다.

systemscheme 필자가 모은 데이터로 fixed effect 회귀를 수행한 결과. (위: 교토의정서 이후 기간, 아래: 전체기간)

필자가 모은 데이터의 경우, 일계차분 회귀에서는 R&D 투자액 축적의 계수가 작아 유의미하지 않았다. 그러므로 일단은, 필자가 복원한 고정효과 모델에서 관측한 변수별 계수 부호가, 에너지경제연구원의 연구 원본에서의 그것과 같음을 확인했음에 의의를 둔다.


코드

패널 분석에 사용한 R 코드는 아래와 같다. 필자가 사용한 데이터셋은 GitHub Repo에 있다. Input 데이터 ($\texttt{energyrnd_rndpercapita.csv}$) 에서 첫 번째 열은 각 국가의 인덱스이며 (즉 서로 다른 숫자가 서로 다른 국가를 의미), 두 번째 열은 연도이다.

rm(list = ls())
setwd(dirname(rstudioapi::getActiveDocumentContext()$path))
scriptpath <- getwd()
cat("\014")

library(plm)
library(lmtest)
library(sandwich)
library(multiwayvcov)

energyrnddat <- read.csv('energyrnd_rndpercapita.csv')
energyrnddat.former <- energyrnddat[energyrnddat$year<1998,] # 교토의정서 이전 기간
energyrnddat.later <- energyrnddat[energyrnddat$year>1997,] # 교토의정서 이후 기간


model.FE.former <- plm(log(ecperpop) ~ log(gdpperpop) + log(eprice) + log(hdd) + log(accrndperpop), data=energyrnddat.former, model="within")
summary(model.FE.former) # Fixed effect regression
coeftest(model.FE.former, vcov=vcovHC(model.FE.former, type="sss", cluster="group")) # 클러스터 표준오차
pwartest(model.FE.former)

model.FE.later <- plm(log(ecperpop) ~ log(gdpperpop) + log(eprice) + log(hdd) + log(accrndperpop), data=energyrnddat.later, model="within")
summary(model.FE.later)
coeftest(model.FE.later, vcov=vcovHC(model.FE.later, type="sss", cluster="group")) 
pwartest(model.FE.later)

model.FE.whole <- plm(log(ecperpop) ~ log(gdpperpop) + log(eprice) + log(hdd) + log(accrndperpop), data=energyrnddat, model="within")
summary(model.FE.whole)
coeftest(model.FE.whole, vcov=vcovHC(model.FE.whole, type="sss", cluster="group")) 
pwartest(model.FE.whole)


model.RE.former <- plm(log(ecperpop) ~ log(gdpperpop) + log(eprice) + log(hdd) + log(accrndperpop), data=energyrnddat.former, model="random")
phtest(model.FE.former, model.RE.former) # Hausman test

model.RE.later <- plm(log(ecperpop) ~ log(gdpperpop) + log(eprice) + log(hdd) + log(accrndperpop), data=energyrnddat.later, model="random")
phtest(model.FE.later, model.RE.later)


model.FD.former <- plm(log(ecperpop) ~ log(gdpperpop) + log(eprice) + log(hdd) + log(accrndperpop), data=energyrnddat.former, model="fd")
summary(model.FD.former) # First-order difference regression

model.FD.later <- plm(log(ecperpop) ~ log(gdpperpop) + log(eprice) + log(hdd) + log(accrndperpop), data=energyrnddat.later, model="fd")
summary(model.FD.later)

model.FD.whole <- plm(log(ecperpop) ~ log(gdpperpop) + log(eprice) + log(hdd) + log(accrndperpop), data=energyrnddat, model="fd")
summary(model.FD.whole)

(위 R 코드 내 메서드들이, 한치록 교수의 “패널데이터강의” 에 나오는 Stata 코드 기반 예제들에 대해 같은 데이터로 같은 결과를 도출함을 확인하였다.)